Towards unlocking the mystery of adversarial fragility of neural networks

In this paper, we study the adversarial robustness of deep neural networks for classification tasks. We look at the smallest magnitude of possible additive perturbations that can change the output of a classification algorithm. We provide a matrix-theoretic explanation of the adversarial fragility of deep neural network for classification. In particular, our theoretical results show that neural network's adversarial robustness can degrade as the input dimension $d$ increases. Analytically we show that neural networks' adversarial robustness can be only $1/\sqrt{d}$ of the best possible adversarial robustness. Our matrix-theoretic explanation is consistent with an earlier information-theoretic feature-compression-based explanation for the adversarial fragility of neural networks.

Outlier Detection Using Generative Models with Theoretical Performance Guarantees

This paper considers the problem of recovering signals modeled by generative models from linear measurements contaminated with sparse outliers. We propose an outlier detection approach for reconstructing the ground-truth signals modeled by generative models under sparse outliers. We establish theoretical recovery guarantees for reconstruction of signals using generative models in the presence of outliers, giving lower bounds on the number of correctable outliers. Our results are applicable to both linear generator neural networks and the nonlinear generator neural networks with an arbitrary number of layers. We propose an iterative alternating direction method of multipliers (ADMM) algorithm for solving the outlier detection problem via $\ell_1$ norm minimization, and a gradient descent algorithm for solving the outlier detection problem via squared $\ell_1$ norm minimization. We conduct extensive experiments using variational auto-encoder and deep convolutional generative adversarial networks, and the experimental results show that the signals can be successfully reconstructed under outliers using our approach. Our approach outperforms the traditional Lasso and $\ell_2$ minimization approach.

Mutual Information Learned Regressor: an Information-theoretic Viewpoint of Training Regression Systems

As one of the central tasks in machine learning, regression finds lots of applications in different fields. An existing common practice for solving regression problems is the mean square error (MSE) minimization approach or its regularized variants which require prior knowledge about the models. Recently, Yi et al., proposed a mutual information based supervised learning framework where they introduced a label entropy regularization which does not require any prior knowledge. When applied to classification tasks and solved via a stochastic gradient descent (SGD) optimization algorithm, their approach achieved significant improvement over the commonly used cross entropy loss and its variants. However, they did not provide a theoretical convergence analysis of the SGD algorithm for the proposed formulation. Besides, applying the framework to regression tasks is nontrivial due to the potentially infinite support set of the label. In this paper, we investigate the regression under the mutual information based supervised learning framework. We first argue that the MSE minimization approach is equivalent to a conditional entropy learning problem, and then propose a mutual information learning formulation for solving regression problems by using a reparameterization technique. For the proposed formulation, we give the convergence analysis of the SGD algorithm for solving it in practice. Finally, we consider a multi-output regression data model where we derive the generalization performance lower bound in terms of the mutual information associated with the underlying data distribution. The result shows that the high dimensionality can be a bless instead of a curse, which is controlled by a threshold. We hope our work will serve as a good starting point for further research on the mutual information based regression.

Mutual Information Learned Classifiers: an Information-theoretic Viewpoint of Training Deep Learning Classification Systems

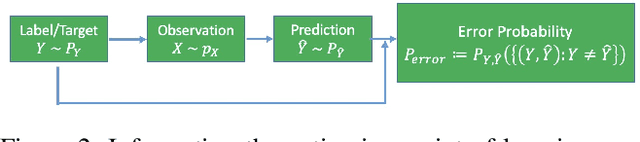
Deep learning systems have been reported to acheive state-of-the-art performances in many applications, and one of the keys for achieving this is the existence of well trained classifiers on benchmark datasets which can be used as backbone feature extractors in downstream tasks. As a main-stream loss function for training deep neural network (DNN) classifiers, the cross entropy loss can easily lead us to find models which demonstrate severe overfitting behavior when no other techniques are used for alleviating it such as data augmentation. In this paper, we prove that the existing cross entropy loss minimization for training DNN classifiers essentially learns the conditional entropy of the underlying data distribution of the dataset, i.e., the information or uncertainty remained in the labels after revealing the input. In this paper, we propose a mutual information learning framework where we train DNN classifiers via learning the mutual information between the label and input. Theoretically, we give the population error probability lower bound in terms of the mutual information. In addition, we derive the mutual information lower and upper bounds for a concrete binary classification data model in $\mbR^n$, and also the error probability lower bound in this scenario. Besides, we establish the sample complexity for accurately learning the mutual information from empirical data samples drawn from the underlying data distribution. Empirically, we conduct extensive experiments on several benchmark datasets to support our theory. Without whistles and bells, the proposed mutual information learned classifiers (MILCs) acheive far better generalization performances than the state-of-the-art classifiers with an improvement which can exceed more than 10\% in testing accuracy.

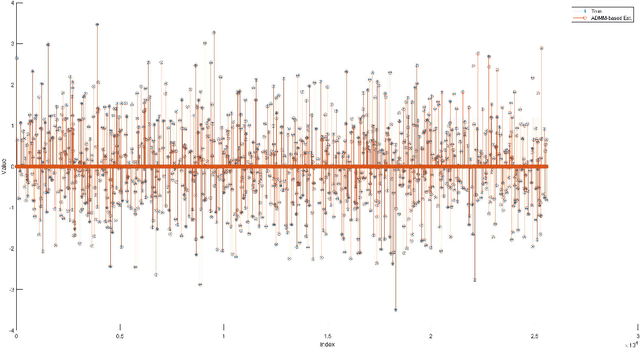
Solving Large Scale Quadratic Constrained Basis Pursuit

Inspired by alternating direction method of multipliers and the idea of operator splitting, we propose a efficient algorithm for solving large-scale quadratically constrained basis pursuit. Experimental results show that the proposed algorithm can achieve 50~~100 times speedup when compared with the baseline interior point algorithm implemented in CVX.

Derivation of Information-Theoretically Optimal Adversarial Attacks with Applications to Robust Machine Learning

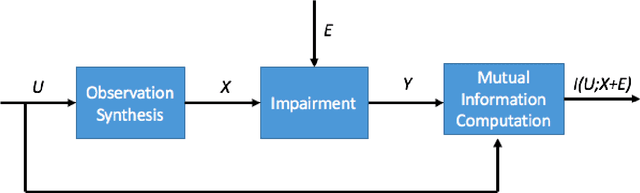
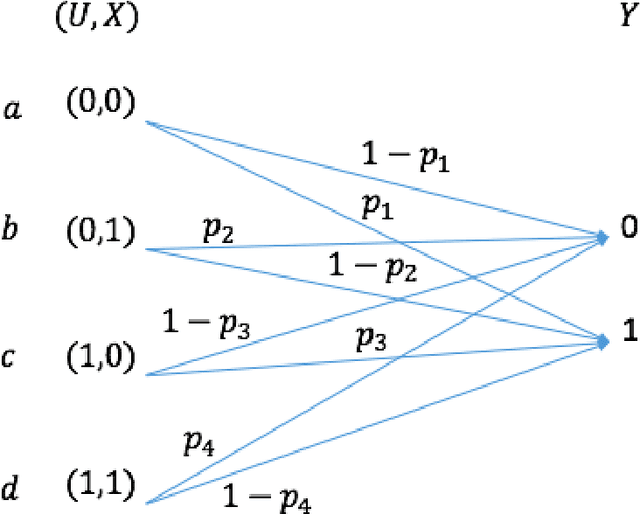
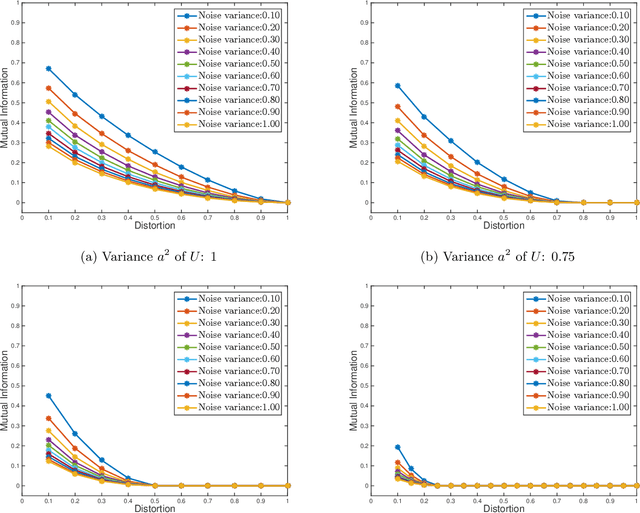
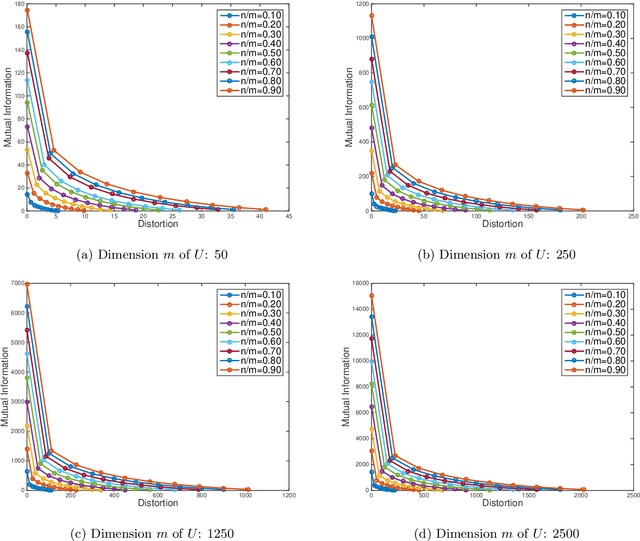
We consider the theoretical problem of designing an optimal adversarial attack on a decision system that maximally degrades the achievable performance of the system as measured by the mutual information between the degraded signal and the label of interest. This problem is motivated by the existence of adversarial examples for machine learning classifiers. By adopting an information theoretic perspective, we seek to identify conditions under which adversarial vulnerability is unavoidable i.e. even optimally designed classifiers will be vulnerable to small adversarial perturbations. We present derivations of the optimal adversarial attacks for discrete and continuous signals of interest, i.e., finding the optimal perturbation distributions to minimize the mutual information between the degraded signal and a signal following a continuous or discrete distribution. In addition, we show that it is much harder to achieve adversarial attacks for minimizing mutual information when multiple redundant copies of the input signal are available. This provides additional support to the recently proposed ``feature compression" hypothesis as an explanation for the adversarial vulnerability of deep learning classifiers. We also report on results from computational experiments to illustrate our theoretical results.

Do Deep Minds Think Alike? Selective Adversarial Attacks for Fine-Grained Manipulation of Multiple Deep Neural Networks

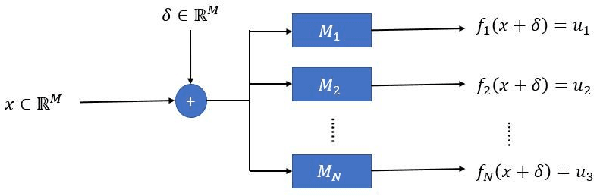
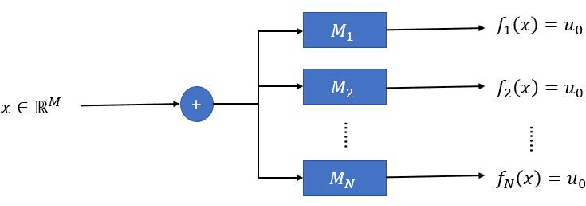
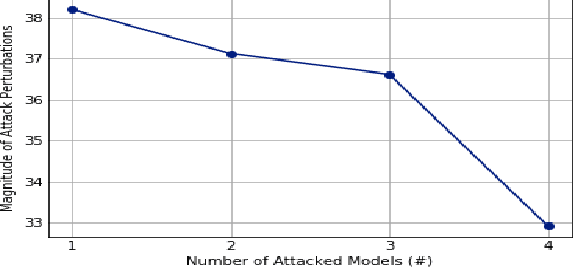
Recent works have demonstrated the existence of {\it adversarial examples} targeting a single machine learning system. In this paper we ask a simple but fundamental question of "selective fooling": given {\it multiple} machine learning systems assigned to solve the same classification problem and taking the same input signal, is it possible to construct a perturbation to the input signal that manipulates the outputs of these {\it multiple} machine learning systems {\it simultaneously} in arbitrary pre-defined ways? For example, is it possible to selectively fool a set of "enemy" machine learning systems but does not fool the other "friend" machine learning systems? The answer to this question depends on the extent to which these different machine learning systems "think alike". We formulate the problem of "selective fooling" as a novel optimization problem, and report on a series of experiments on the MNIST dataset. Our preliminary findings from these experiments show that it is in fact very easy to selectively manipulate multiple MNIST classifiers simultaneously, even when the classifiers are identical in their architectures, training algorithms and training datasets except for random initialization during training. This suggests that two nominally equivalent machine learning systems do not in fact "think alike" at all, and opens the possibility for many novel applications and deeper understandings of the working principles of deep neural networks.

Trust but Verify: An Information-Theoretic Explanation for the Adversarial Fragility of Machine Learning Systems, and a General Defense against Adversarial Attacks

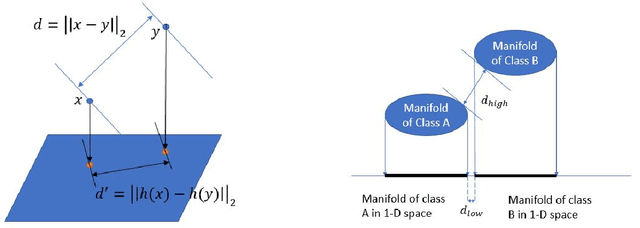
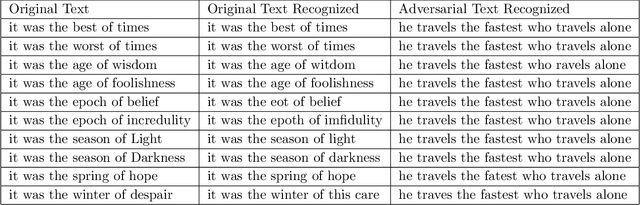
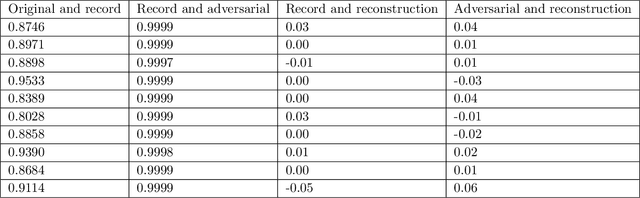
Deep-learning based classification algorithms have been shown to be susceptible to adversarial attacks: minor changes to the input of classifiers can dramatically change their outputs, while being imperceptible to humans. In this paper, we present a simple hypothesis about a feature compression property of artificial intelligence (AI) classifiers and present theoretical arguments to show that this hypothesis successfully accounts for the observed fragility of AI classifiers to small adversarial perturbations. Drawing on ideas from information and coding theory, we propose a general class of defenses for detecting classifier errors caused by abnormally small input perturbations. We further show theoretical guarantees for the performance of this detection method. We present experimental results with (a) a voice recognition system, and (b) a digit recognition system using the MNIST database, to demonstrate the effectiveness of the proposed defense methods. The ideas in this paper are motivated by a simple analogy between AI classifiers and the standard Shannon model of a communication system.

An Information-Theoretic Explanation for the Adversarial Fragility of AI Classifiers

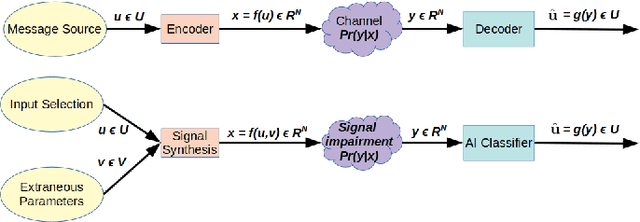
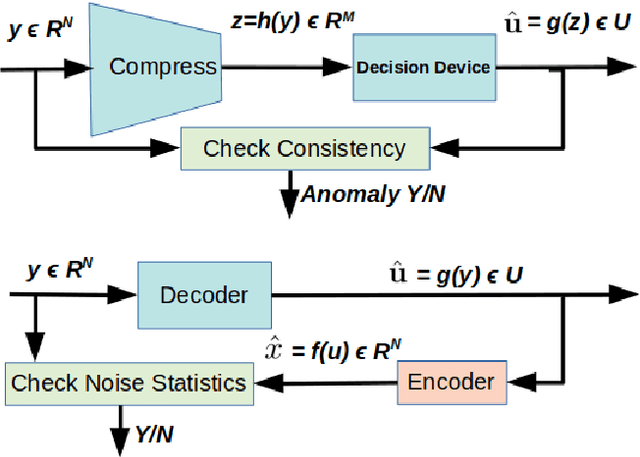
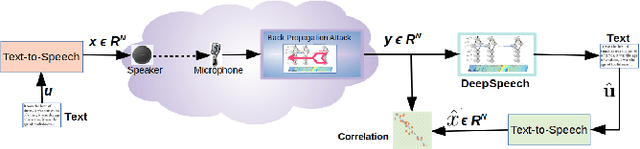
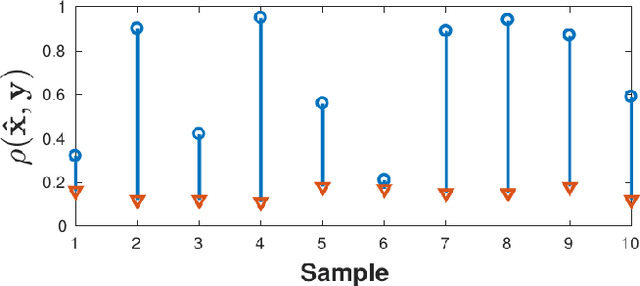
We present a simple hypothesis about a compression property of artificial intelligence (AI) classifiers and present theoretical arguments to show that this hypothesis successfully accounts for the observed fragility of AI classifiers to small adversarial perturbations. We also propose a new method for detecting when small input perturbations cause classifier errors, and show theoretical guarantees for the performance of this detection method. We present experimental results with a voice recognition system to demonstrate this method. The ideas in this paper are motivated by a simple analogy between AI classifiers and the standard Shannon model of a communication system.

Outlier Detection using Generative Models with Theoretical Performance Guarantees

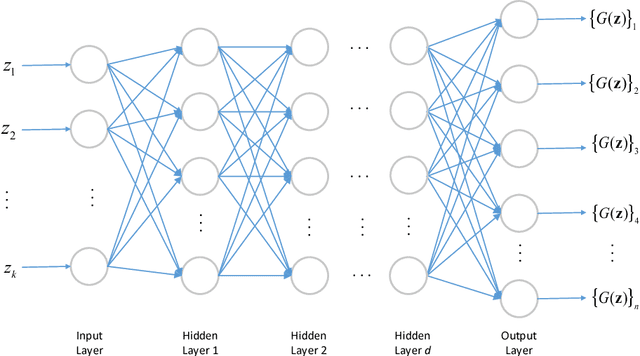
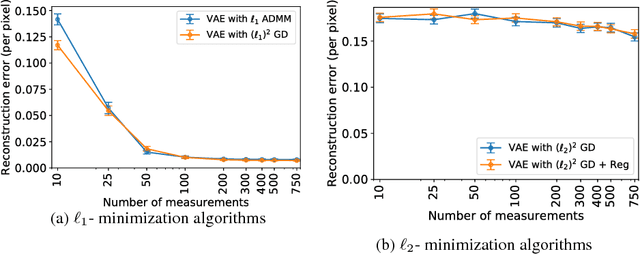
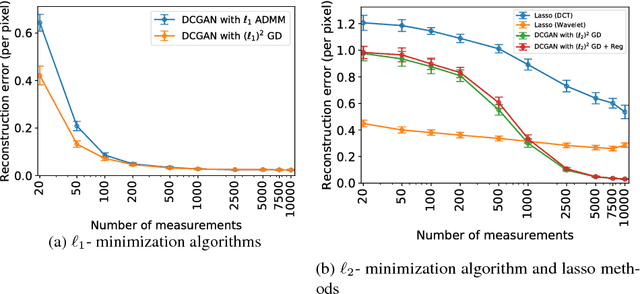
This paper considers the problem of recovering signals from compressed measurements contaminated with sparse outliers, which has arisen in many applications. In this paper, we propose a generative model neural network approach for reconstructing the ground truth signals under sparse outliers. We propose an iterative alternating direction method of multipliers (ADMM) algorithm for solving the outlier detection problem via $\ell_1$ norm minimization, and a gradient descent algorithm for solving the outlier detection problem via squared $\ell_1$ norm minimization. We establish the recovery guarantees for reconstruction of signals using generative models in the presence of outliers, and give an upper bound on the number of outliers allowed for recovery. Our results are applicable to both the linear generator neural network and the nonlinear generator neural network with an arbitrary number of layers. We conduct extensive experiments using variational auto-encoder and deep convolutional generative adversarial networks, and the experimental results show that the signals can be successfully reconstructed under outliers using our approach. Our approach outperforms the traditional Lasso and $\ell_2$ minimization approach.