Orthogonal Estimation of Wasserstein Distances

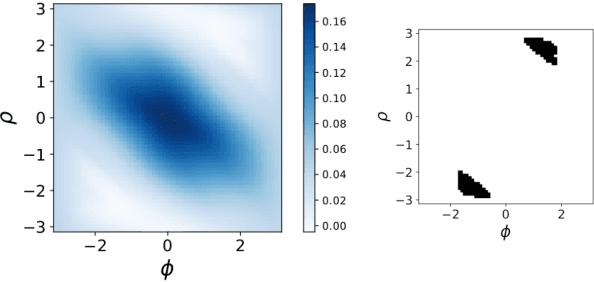
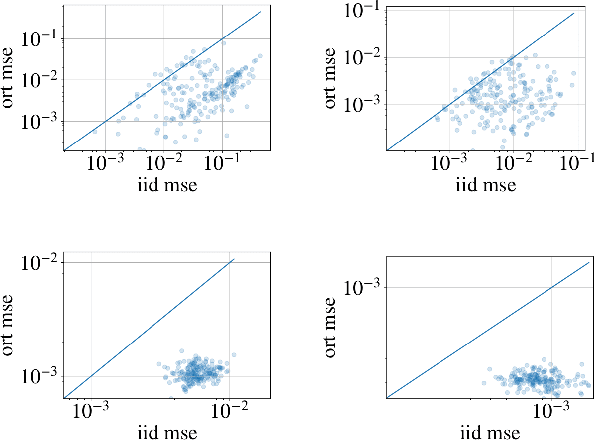
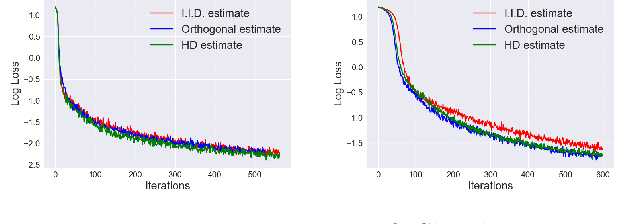
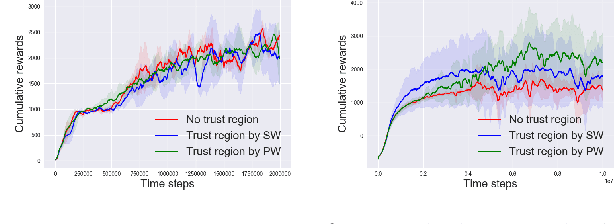
Wasserstein distances are increasingly used in a wide variety of applications in machine learning. Sliced Wasserstein distances form an important subclass which may be estimated efficiently through one-dimensional sorting operations. In this paper, we propose a new variant of sliced Wasserstein distance, study the use of orthogonal coupling in Monte Carlo estimation of Wasserstein distances and draw connections with stratified sampling, and evaluate our approaches experimentally in a range of large-scale experiments in generative modelling and reinforcement learning.

Successor Uncertainties: exploration and uncertainty in temporal difference learning

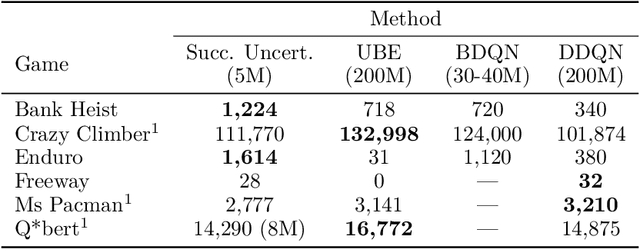
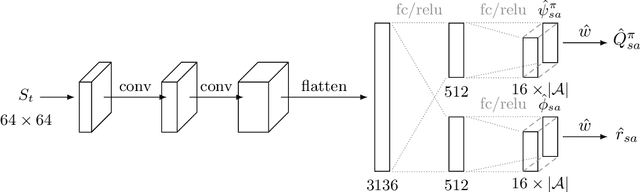
We consider the problem of balancing exploration and exploitation in sequential decision making problems. To explore efficiently, it is vital to consider the uncertainty over all consequences of a decision, and not just those that follow immediately; the uncertainties involved need to be propagated according to the dynamics of the problem. To this end, we develop Successor Uncertainties, a probabilistic model for the state-action value function of a Markov Decision Process that propagates uncertainties in a coherent and scalable way. We relate our approach to other classical and contemporary methods for exploration and present an empirical analysis.

Gaussian Process Behaviour in Wide Deep Neural Networks

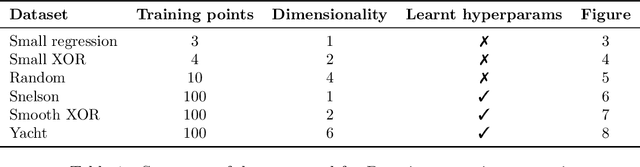
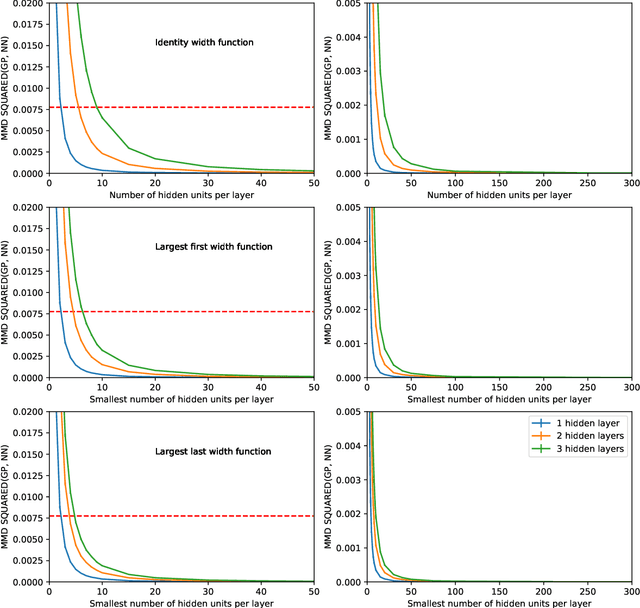
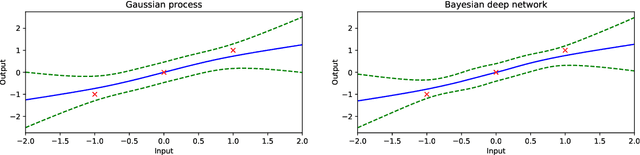
Whilst deep neural networks have shown great empirical success, there is still much work to be done to understand their theoretical properties. In this paper, we study the relationship between random, wide, fully connected, feedforward networks with more than one hidden layer and Gaussian processes with a recursive kernel definition. We show that, under broad conditions, as we make the architecture increasingly wide, the implied random function converges in distribution to a Gaussian process, formalising and extending existing results by Neal (1996) to deep networks. To evaluate convergence rates empirically, we use maximum mean discrepancy. We then compare finite Bayesian deep networks from the literature to Gaussian processes in terms of the key predictive quantities of interest, finding that in some cases the agreement can be very close. We discuss the desirability of Gaussian process behaviour and review non-Gaussian alternative models from the literature.

Variational Bayesian dropout: pitfalls and fixes

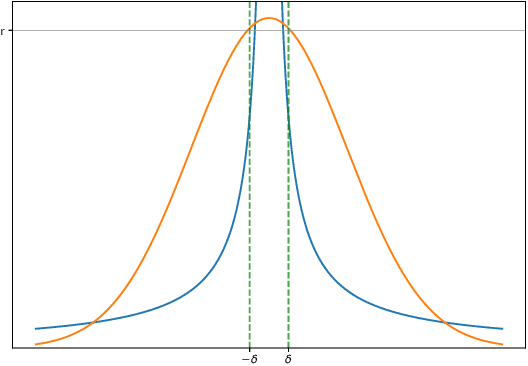
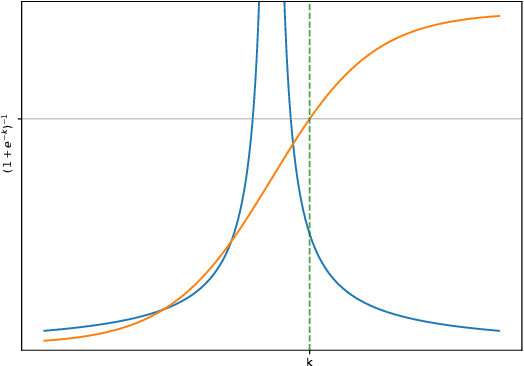
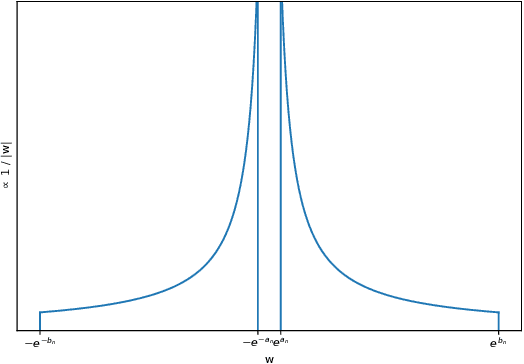
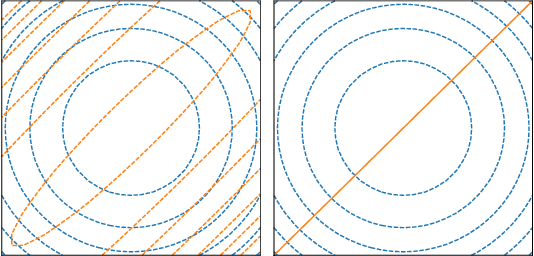
Dropout, a stochastic regularisation technique for training of neural networks, has recently been reinterpreted as a specific type of approximate inference algorithm for Bayesian neural networks. The main contribution of the reinterpretation is in providing a theoretical framework useful for analysing and extending the algorithm. We show that the proposed framework suffers from several issues; from undefined or pathological behaviour of the true posterior related to use of improper priors, to an ill-defined variational objective due to singularity of the approximating distribution relative to the true posterior. Our analysis of the improper log uniform prior used in variational Gaussian dropout suggests the pathologies are generally irredeemable, and that the algorithm still works only because the variational formulation annuls some of the pathologies. To address the singularity issue, we proffer Quasi-KL (QKL) divergence, a new approximate inference objective for approximation of high-dimensional distributions. We show that motivations for variational Bernoulli dropout based on discretisation and noise have QKL as a limit. Properties of QKL are studied both theoretically and on a simple practical example which shows that the QKL-optimal approximation of a full rank Gaussian with a degenerate one naturally leads to the Principal Component Analysis solution.

Variational Gaussian Dropout is not Bayesian

Gaussian multiplicative noise is commonly used as a stochastic regularisation technique in training of deterministic neural networks. A recent paper reinterpreted the technique as a specific algorithm for approximate inference in Bayesian neural networks; several extensions ensued. We show that the log-uniform prior used in all the above publications does not generally induce a proper posterior, and thus Bayesian inference in such models is ill-posed. Independent of the log-uniform prior, the correlated weight noise approximation has further issues leading to either infinite objective or high risk of overfitting. The above implies that the reported sparsity of obtained solutions cannot be explained by Bayesian or the related minimum description length arguments. We thus study the objective from a non-Bayesian perspective, provide its previously unknown analytical form which allows exact gradient evaluation, and show that the later proposed additive reparametrisation introduces minima not present in the original multiplicative parametrisation. Implications and future research directions are discussed.

Concrete Dropout

Dropout is used as a practical tool to obtain uncertainty estimates in large vision models and reinforcement learning (RL) tasks. But to obtain well-calibrated uncertainty estimates, a grid-search over the dropout probabilities is necessary - a prohibitive operation with large models, and an impossible one with RL. We propose a new dropout variant which gives improved performance and better calibrated uncertainties. Relying on recent developments in Bayesian deep learning, we use a continuous relaxation of dropout's discrete masks. Together with a principled optimisation objective, this allows for automatic tuning of the dropout probability in large models, and as a result faster experimentation cycles. In RL this allows the agent to adapt its uncertainty dynamically as more data is observed. We analyse the proposed variant extensively on a range of tasks, and give insights into common practice in the field where larger dropout probabilities are often used in deeper model layers.