Byzantine-Resilient Decentralized Multi-Armed Bandits

In decentralized cooperative multi-armed bandits (MAB), each agent observes a distinct stream of rewards, and seeks to exchange information with others to select a sequence of arms so as to minimize its regret. Agents in the cooperative setting can outperform a single agent running a MAB method such as Upper-Confidence Bound (UCB) independently. In this work, we study how to recover such salient behavior when an unknown fraction of the agents can be Byzantine, that is, communicate arbitrarily wrong information in the form of reward mean-estimates or confidence sets. This framework can be used to model attackers in computer networks, instigators of offensive content into recommender systems, or manipulators of financial markets. Our key contribution is the development of a fully decentralized resilient upper confidence bound (UCB) algorithm that fuses an information mixing step among agents with a truncation of inconsistent and extreme values. This truncation step enables us to establish that the performance of each normal agent is no worse than the classic single-agent UCB1 algorithm in terms of regret, and more importantly, the cumulative regret of all normal agents is strictly better than the non-cooperative case, provided that each agent has at least 3f+1 neighbors where f is the maximum possible Byzantine agents in each agent's neighborhood. Extensions to time-varying neighbor graphs, and minimax lower bounds are further established on the achievable regret. Experiments corroborate the merits of this framework in practice.

Decentralized Multi-Armed Bandit Can Outperform Classic Upper Confidence Bound

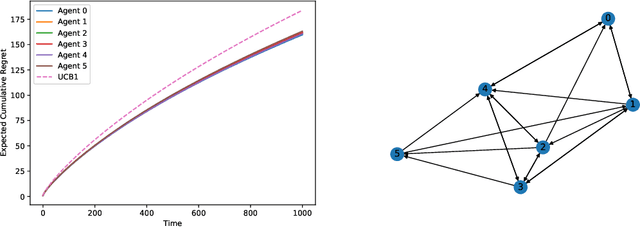
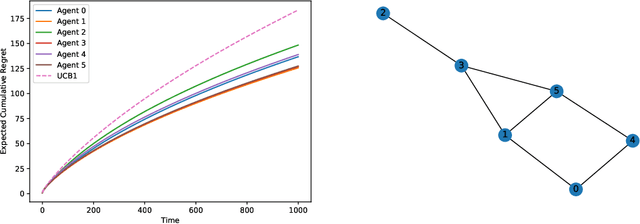
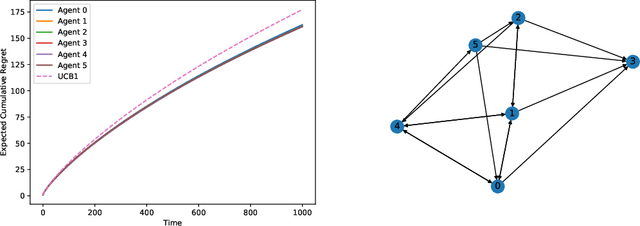
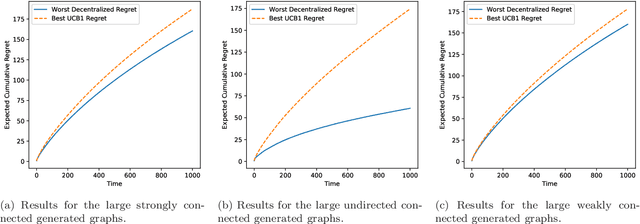
This paper studies a decentralized multi-armed bandit problem in a multi-agent network. The problem is simultaneously solved by N agents assuming they face a common set of M arms and share the same mean of each arm's reward. Each agent can receive information only from its neighbors, where the neighbor relations among the agents are described by a directed graph whose vertices represent agents and whose directed edges depict neighbor relations. A fully decentralized multi-armed bandit algorithm is proposed for each agent, which twists the classic consensus algorithm and upper confidence bound (UCB) algorithm. It is shown that the algorithm guarantees each agent to achieve a better logarithmic asymptotic regret than the classic UCB provided the neighbor graph is strongly connected. The regret can be further improved if the neighbor graph is undirected.

Federated Bandit: A Gossiping Approach

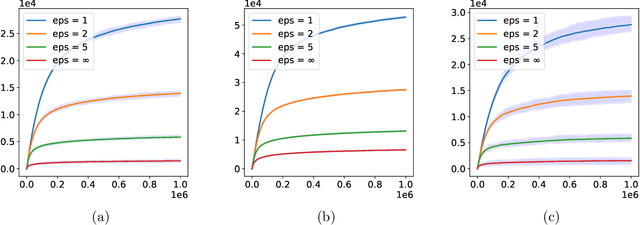
In this paper, we study \emph{Federated Bandit}, a decentralized Multi-Armed Bandit problem with a set of $N$ agents, who can only communicate their local data with neighbors described by a connected graph $G$. Each agent makes a sequence of decisions on selecting an arm from $M$ candidates, yet they only have access to local and potentially biased feedback/evaluation of the true reward for each action taken. Learning only locally will lead agents to sub-optimal actions while converging to a no-regret strategy requires a collection of distributed data. Motivated by the proposal of federated learning, we aim for a solution with which agents will never share their local observations with a central entity, and will be allowed to only share a private copy of his/her own information with their neighbors. We first propose a decentralized bandit algorithm \texttt{Gossip\_UCB}, which is a coupling of variants of both the classical gossiping algorithm and the celebrated Upper Confidence Bound (UCB) bandit algorithm. We show that \texttt{Gossip\_UCB} successfully adapts local bandit learning into a global gossiping process for sharing information among connected agents, and achieves guaranteed regret at the order of $O(\max\{ \texttt{poly}(N,M) \log T, \texttt{poly}(N,M)\log_{\lambda_2^{-1}} N\})$ for all $N$ agents, where $\lambda_2\in(0,1)$ is the second largest eigenvalue of the expected gossip matrix, which is a function of $G$. We then propose \texttt{Fed\_UCB}, a differentially private version of \texttt{Gossip\_UCB}, in which the agents preserve $\epsilon$-differential privacy of their local data while achieving $O(\max \{\frac{\texttt{poly}(N,M)}{\epsilon}\log^{2.5} T, \texttt{poly}(N,M) (\log_{\lambda_2^{-1}} N + \log T) \})$ regret.