HiPreNets: High-Precision Neural Networks through Progressive Training

Deep neural networks are powerful tools for solving nonlinear problems in science and engineering, but training highly accurate models becomes challenging as problem complexity increases. Non-convex optimization and numerous hyperparameters to tune make performance improvement difficult, and traditional approaches often prioritize minimizing mean squared error (MSE) while overlooking $L^{\infty}$ error, which is the critical focus in many applications. To address these challenges, we present a progressive framework for training and tuning high-precision neural networks (HiPreNets). Our approach refines a previously explored staged training technique for neural networks that improves an existing fully connected neural network by sequentially learning its prediction residuals using additional networks, leading to improved overall accuracy. We discuss how to take advantage of the structure of the residuals to guide the choice of loss function, number of parameters to use, and ways to introduce adaptive data sampling techniques. We validate our framework's effectiveness through several benchmark problems.

Decentralized Multi-Armed Bandit Can Outperform Classic Upper Confidence Bound

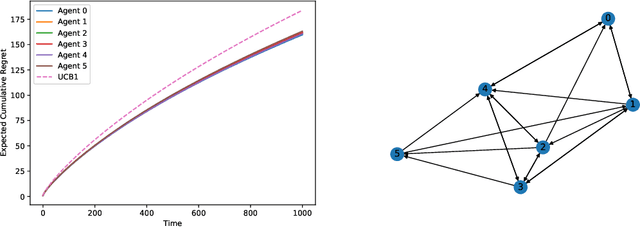
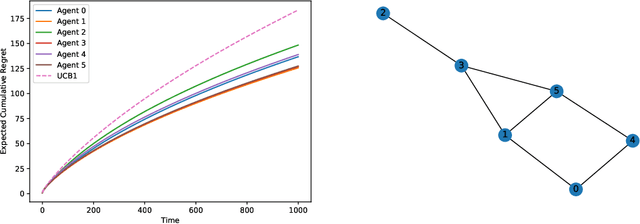
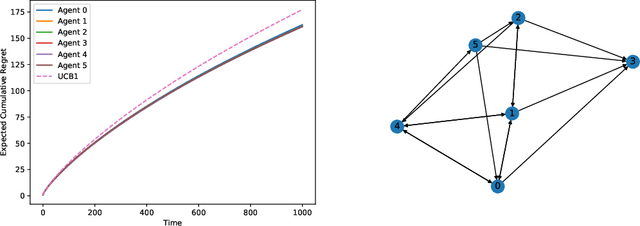
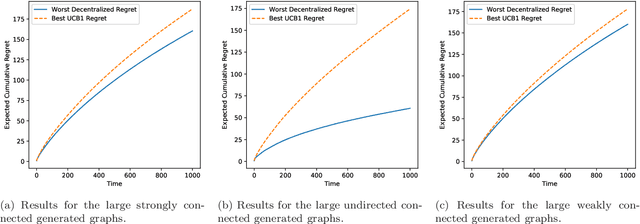
This paper studies a decentralized multi-armed bandit problem in a multi-agent network. The problem is simultaneously solved by N agents assuming they face a common set of M arms and share the same mean of each arm's reward. Each agent can receive information only from its neighbors, where the neighbor relations among the agents are described by a directed graph whose vertices represent agents and whose directed edges depict neighbor relations. A fully decentralized multi-armed bandit algorithm is proposed for each agent, which twists the classic consensus algorithm and upper confidence bound (UCB) algorithm. It is shown that the algorithm guarantees each agent to achieve a better logarithmic asymptotic regret than the classic UCB provided the neighbor graph is strongly connected. The regret can be further improved if the neighbor graph is undirected.