LLM-Powered CPI Prediction Inference with Online Text Time Series

Forecasting the Consumer Price Index (CPI) is an important yet challenging task in economics, where most existing approaches rely on low-frequency, survey-based data. With the recent advances of large language models (LLMs), there is growing potential to leverage high-frequency online text data for improved CPI prediction, an area still largely unexplored. This paper proposes LLM-CPI, an LLM-based approach for CPI prediction inference incorporating online text time series. We collect a large set of high-frequency online texts from a popularly used Chinese social network site and employ LLMs such as ChatGPT and the trained BERT models to construct continuous inflation labels for posts that are related to inflation. Online text embeddings are extracted via LDA and BERT. We develop a joint time series framework that combines monthly CPI data with LLM-generated daily CPI surrogates. The monthly model employs an ARX structure combining observed CPI data with text embeddings and macroeconomic variables, while the daily model uses a VARX structure built on LLM-generated CPI surrogates and text embeddings. We establish the asymptotic properties of the method and provide two forms of constructed prediction intervals. The finite-sample performance and practical advantages of LLM-CPI are demonstrated through both simulation and real data examples.

SOFARI-R: High-Dimensional Manifold-Based Inference for Latent Responses

Data reduction with uncertainty quantification plays a key role in various multi-task learning applications, where large numbers of responses and features are present. To this end, a general framework of high-dimensional manifold-based SOFAR inference (SOFARI) was introduced recently in Zheng, Zhou, Fan and Lv (2024) for interpretable multi-task learning inference focusing on the left factor vectors and singular values exploiting the latent singular value decomposition (SVD) structure. Yet, designing a valid inference procedure on the latent right factor vectors is not straightforward from that of the left ones and can be even more challenging due to asymmetry of left and right singular vectors in the response matrix. To tackle these issues, in this paper we suggest a new method of high-dimensional manifold-based SOFAR inference for latent responses (SOFARI-R), where two variants of SOFARI-R are introduced. The first variant deals with strongly orthogonal factors by coupling left singular vectors with the design matrix and then appropriately rescaling them to generate new Stiefel manifolds. The second variant handles the more general weakly orthogonal factors by employing the hard-thresholded SOFARI estimates and delicately incorporating approximation errors into the distribution. Both variants produce bias-corrected estimators for the latent right factor vectors that enjoy asymptotically normal distributions with justified asymptotic variance estimates. We demonstrate the effectiveness of the newly suggested method using extensive simulation studies and an economic application.

Asymptotic FDR Control with Model-X Knockoffs: Is Moments Matching Sufficient?

We propose a unified theoretical framework for studying the robustness of the model-X knockoffs framework by investigating the asymptotic false discovery rate (FDR) control of the practically implemented approximate knockoffs procedure. This procedure deviates from the model-X knockoffs framework by substituting the true covariate distribution with a user-specified distribution that can be learned using in-sample observations. By replacing the distributional exchangeability condition of the model-X knockoff variables with three conditions on the approximate knockoff statistics, we establish that the approximate knockoffs procedure achieves the asymptotic FDR control. Using our unified framework, we further prove that an arguably most popularly used knockoff variable generation method--the Gaussian knockoffs generator based on the first two moments matching--achieves the asymptotic FDR control when the two-moment-based knockoff statistics are employed in the knockoffs inference procedure. For the first time in the literature, our theoretical results justify formally the effectiveness and robustness of the Gaussian knockoffs generator. Simulation and real data examples are conducted to validate the theoretical findings.

HNCI: High-Dimensional Network Causal Inference

The problem of evaluating the effectiveness of a treatment or policy commonly appears in causal inference applications under network interference. In this paper, we suggest the new method of high-dimensional network causal inference (HNCI) that provides both valid confidence interval on the average direct treatment effect on the treated (ADET) and valid confidence set for the neighborhood size for interference effect. We exploit the model setting in Belloni et al. (2022) and allow certain type of heterogeneity in node interference neighborhood sizes. We propose a linear regression formulation of potential outcomes, where the regression coefficients correspond to the underlying true interference function values of nodes and exhibit a latent homogeneous structure. Such a formulation allows us to leverage existing literature from linear regression and homogeneity pursuit to conduct valid statistical inferences with theoretical guarantees. The resulting confidence intervals for the ADET are formally justified through asymptotic normalities with estimable variances. We further provide the confidence set for the neighborhood size with theoretical guarantees exploiting the repro samples approach. The practical utilities of the newly suggested methods are demonstrated through simulation and real data examples.

Exogenous Randomness Empowering Random Forests

We offer theoretical and empirical insights into the impact of exogenous randomness on the effectiveness of random forests with tree-building rules independent of training data. We formally introduce the concept of exogenous randomness and identify two types of commonly existing randomness: Type I from feature subsampling, and Type II from tie-breaking in tree-building processes. We develop non-asymptotic expansions for the mean squared error (MSE) for both individual trees and forests and establish sufficient and necessary conditions for their consistency. In the special example of the linear regression model with independent features, our MSE expansions are more explicit, providing more understanding of the random forests' mechanisms. It also allows us to derive an upper bound on the MSE with explicit consistency rates for trees and forests. Guided by our theoretical findings, we conduct simulations to further explore how exogenous randomness enhances random forest performance. Our findings unveil that feature subsampling reduces both the bias and variance of random forests compared to individual trees, serving as an adaptive mechanism to balance bias and variance. Furthermore, our results reveal an intriguing phenomenon: the presence of noise features can act as a "blessing" in enhancing the performance of random forests thanks to feature subsampling.

DeepLINK-T: deep learning inference for time series data using knockoffs and LSTM

High-dimensional longitudinal time series data is prevalent across various real-world applications. Many such applications can be modeled as regression problems with high-dimensional time series covariates. Deep learning has been a popular and powerful tool for fitting these regression models. Yet, the development of interpretable and reproducible deep-learning models is challenging and remains underexplored. This study introduces a novel method, Deep Learning Inference using Knockoffs for Time series data (DeepLINK-T), focusing on the selection of significant time series variables in regression while controlling the false discovery rate (FDR) at a predetermined level. DeepLINK-T combines deep learning with knockoff inference to control FDR in feature selection for time series models, accommodating a wide variety of feature distributions. It addresses dependencies across time and features by leveraging a time-varying latent factor structure in time series covariates. Three key ingredients for DeepLINK-T are 1) a Long Short-Term Memory (LSTM) autoencoder for generating time series knockoff variables, 2) an LSTM prediction network using both original and knockoff variables, and 3) the application of the knockoffs framework for variable selection with FDR control. Extensive simulation studies have been conducted to evaluate DeepLINK-T's performance, showing its capability to control FDR effectively while demonstrating superior feature selection power for high-dimensional longitudinal time series data compared to its non-time series counterpart. DeepLINK-T is further applied to three metagenomic data sets, validating its practical utility and effectiveness, and underscoring its potential in real-world applications.

SOFARI: High-Dimensional Manifold-Based Inference

Multi-task learning is a widely used technique for harnessing information from various tasks. Recently, the sparse orthogonal factor regression (SOFAR) framework, based on the sparse singular value decomposition (SVD) within the coefficient matrix, was introduced for interpretable multi-task learning, enabling the discovery of meaningful latent feature-response association networks across different layers. However, conducting precise inference on the latent factor matrices has remained challenging due to orthogonality constraints inherited from the sparse SVD constraint. In this paper, we suggest a novel approach called high-dimensional manifold-based SOFAR inference (SOFARI), drawing on the Neyman near-orthogonality inference while incorporating the Stiefel manifold structure imposed by the SVD constraints. By leveraging the underlying Stiefel manifold structure, SOFARI provides bias-corrected estimators for both latent left factor vectors and singular values, for which we show to enjoy the asymptotic mean-zero normal distributions with estimable variances. We introduce two SOFARI variants to handle strongly and weakly orthogonal latent factors, where the latter covers a broader range of applications. We illustrate the effectiveness of SOFARI and justify our theoretical results through simulation examples and a real data application in economic forecasting.

ARK: Robust Knockoffs Inference with Coupling

We investigate the robustness of the model-X knockoffs framework with respect to the misspecified or estimated feature distribution. We achieve such a goal by theoretically studying the feature selection performance of a practically implemented knockoffs algorithm, which we name as the approximate knockoffs (ARK) procedure, under the measures of the false discovery rate (FDR) and family wise error rate (FWER). The approximate knockoffs procedure differs from the model-X knockoffs procedure only in that the former uses the misspecified or estimated feature distribution. A key technique in our theoretical analyses is to couple the approximate knockoffs procedure with the model-X knockoffs procedure so that random variables in these two procedures can be close in realizations. We prove that if such coupled model-X knockoffs procedure exists, the approximate knockoffs procedure can achieve the asymptotic FDR or FWER control at the target level. We showcase three specific constructions of such coupled model-X knockoff variables, verifying their existence and justifying the robustness of the model-X knockoffs framework.

SIMPLE-RC: Group Network Inference with Non-Sharp Nulls and Weak Signals

Large-scale network inference with uncertainty quantification has important applications in natural, social, and medical sciences. The recent work of Fan, Fan, Han and Lv (2022) introduced a general framework of statistical inference on membership profiles in large networks (SIMPLE) for testing the sharp null hypothesis that a pair of given nodes share the same membership profiles. In real applications, there are often groups of nodes under investigation that may share similar membership profiles at the presence of relatively weaker signals than the setting considered in SIMPLE. To address these practical challenges, in this paper we propose a SIMPLE method with random coupling (SIMPLE-RC) for testing the non-sharp null hypothesis that a group of given nodes share similar (not necessarily identical) membership profiles under weaker signals. Utilizing the idea of random coupling, we construct our test as the maximum of the SIMPLE tests for subsampled node pairs from the group. Such technique reduces significantly the correlation among individual SIMPLE tests while largely maintaining the power, enabling delicate analysis on the asymptotic distributions of the SIMPLE-RC test. Our method and theory cover both the cases with and without node degree heterogeneity. These new theoretical developments are empowered by a second-order expansion of spiked eigenvectors under the $\ell_\infty$-norm, built upon our work for random matrices with weak spikes. Our theoretical results and the practical advantages of the newly suggested method are demonstrated through several simulation and real data examples.

FACT: High-Dimensional Random Forests Inference

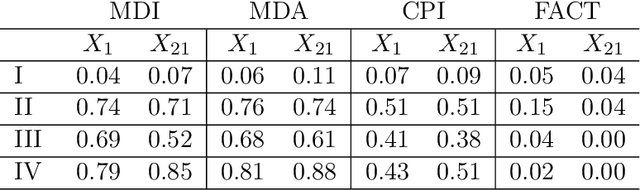
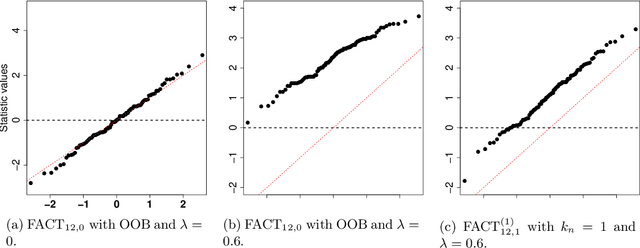
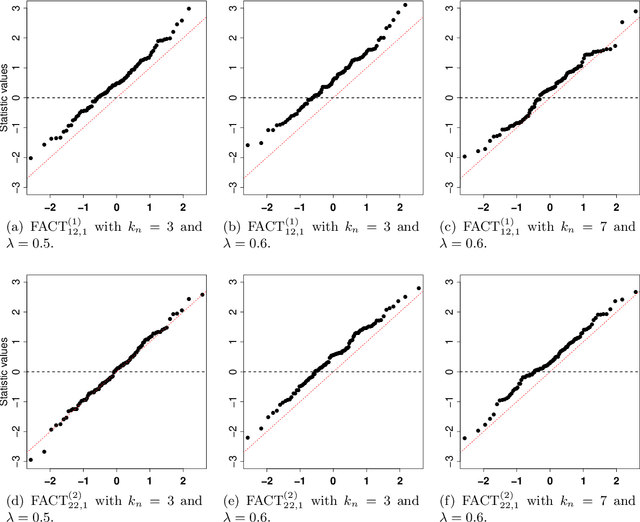
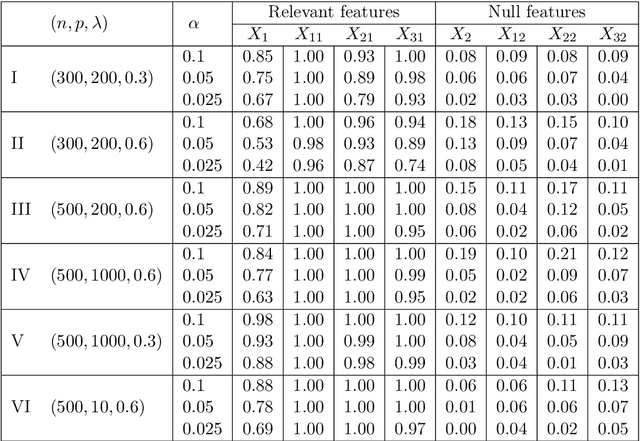
Random forests is one of the most widely used machine learning methods over the past decade thanks to its outstanding empirical performance. Yet, because of its black-box nature, the results by random forests can be hard to interpret in many big data applications. Quantifying the usefulness of individual features in random forests learning can greatly enhance its interpretability. Existing studies have shown that some popularly used feature importance measures for random forests suffer from the bias issue. In addition, there lack comprehensive size and power analyses for most of these existing methods. In this paper, we approach the problem via hypothesis testing, and suggest a framework of the self-normalized feature-residual correlation test (FACT) for evaluating the significance of a given feature in the random forests model with bias-resistance property, where our null hypothesis concerns whether the feature is conditionally independent of the response given all other features. Such an endeavor on random forests inference is empowered by some recent developments on high-dimensional random forests consistency. The vanilla version of our FACT test can suffer from the bias issue in the presence of feature dependency. We exploit the techniques of imbalancing and conditioning for bias correction. We further incorporate the ensemble idea into the FACT statistic through feature transformations for the enhanced power. Under a fairly general high-dimensional nonparametric model setting with dependent features, we formally establish that FACT can provide theoretically justified random forests feature p-values and enjoy appealing power through nonasymptotic analyses. The theoretical results and finite-sample advantages of the newly suggested method are illustrated with several simulation examples and an economic forecasting application in relation to COVID-19.