On the Maximum Hessian Eigenvalue and Generalization

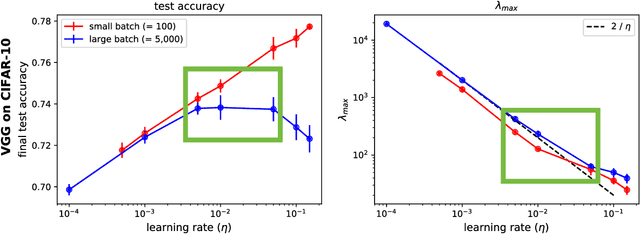
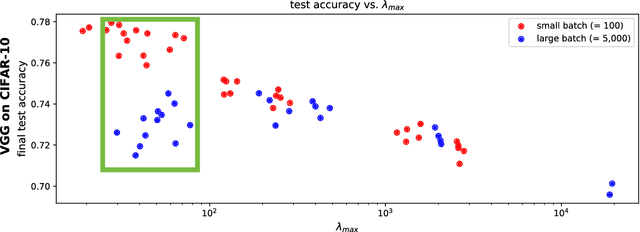
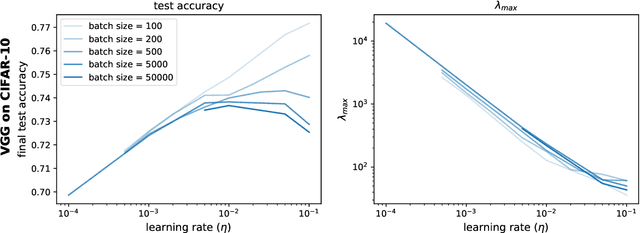
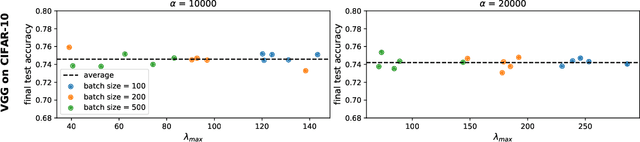
The mechanisms by which certain training interventions, such as increasing learning rates and applying batch normalization, improve the generalization of deep networks remains a mystery. Prior works have speculated that "flatter" solutions generalize better than "sharper" solutions to unseen data, motivating several metrics for measuring flatness (particularly $\lambda_{max}$, the largest eigenvalue of the Hessian of the loss); and algorithms, such as Sharpness-Aware Minimization (SAM) [1], that directly optimize for flatness. Other works question the link between $\lambda_{max}$ and generalization. In this paper, we present findings that call $\lambda_{max}$'s influence on generalization further into question. We show that: (1) while larger learning rates reduce $\lambda_{max}$ for all batch sizes, generalization benefits sometimes vanish at larger batch sizes; (2) by scaling batch size and learning rate simultaneously, we can change $\lambda_{max}$ without affecting generalization; (3) while SAM produces smaller $\lambda_{max}$ for all batch sizes, generalization benefits (also) vanish with larger batch sizes; (4) for dropout, excessively high dropout probabilities can degrade generalization, even as they promote smaller $\lambda_{max}$; and (5) while batch-normalization does not consistently produce smaller $\lambda_{max}$, it nevertheless confers generalization benefits. While our experiments affirm the generalization benefits of large learning rates and SAM for minibatch SGD, the GD-SGD discrepancy demonstrates limits to $\lambda_{max}$'s ability to explain generalization in neural networks.

Multi-Channel Automatic Music Transcription Using Tensor Algebra

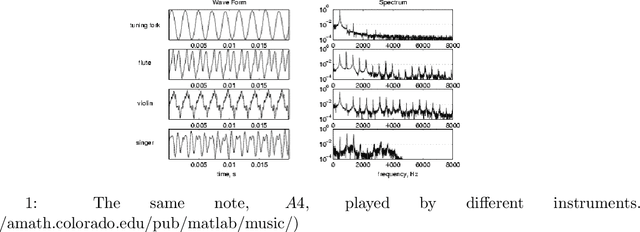
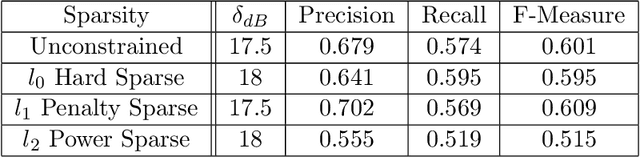
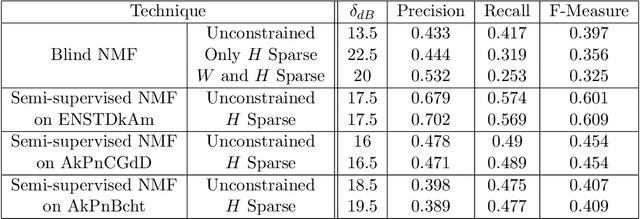
Music is an art, perceived in unique ways by every listener, coming from acoustic signals. In the meantime, standards as musical scores exist to describe it. Even if humans can make this transcription, it is costly in terms of time and efforts, even more with the explosion of information consecutively to the rise of the Internet. In that sense, researches are driven in the direction of Automatic Music Transcription. While this task is considered solved in the case of single notes, it is still open when notes superpose themselves, forming chords. This report aims at developing some of the existing techniques towards Music Transcription, particularly matrix factorization, and introducing the concept of multi-channel automatic music transcription. This concept will be explored with mathematical objects called tensors.

Robot Design With Neural Networks, MILP Solvers and Active Learning

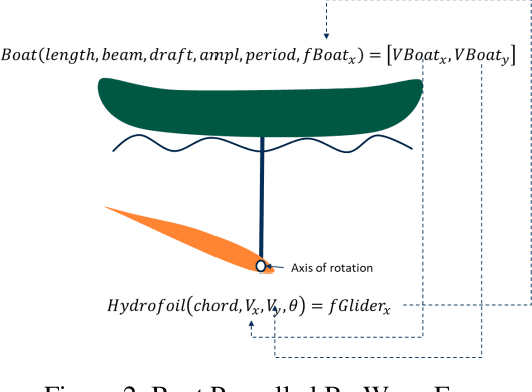
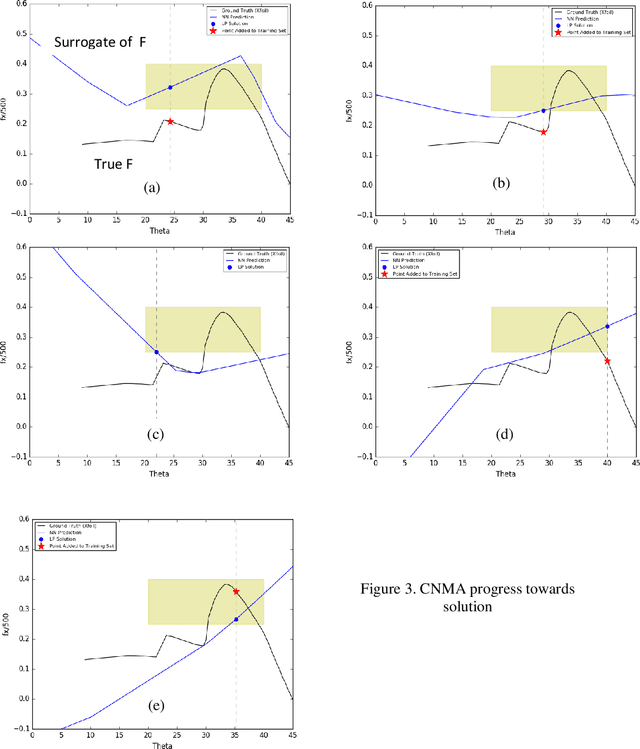
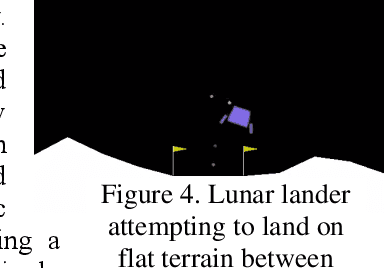
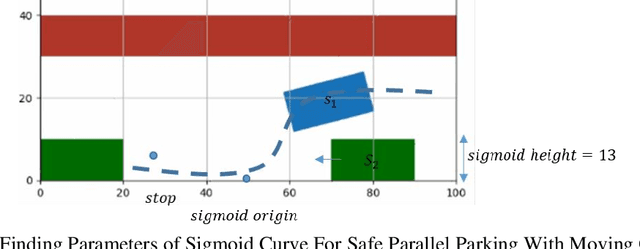
Central to the design of many robot systems and their controllers is solving a constrained blackbox optimization problem. This paper presents CNMA, a new method of solving this problem that is conservative in the number of potentially expensive blackbox function evaluations; allows specifying complex, even recursive constraints directly rather than as hard-to-design penalty or barrier functions; and is resilient to the non-termination of function evaluations. CNMA leverages the ability of neural networks to approximate any continuous function, their transformation into equivalent mixed integer linear programs (MILPs) and their optimization subject to constraints with industrial strength MILP solvers. A new learning-from-failure step guides the learning to be relevant to solving the constrained optimization problem. Thus, the amount of learning is orders of magnitude smaller than that needed to learn functions over their entire domains. CNMA is illustrated with the design of several robotic systems: wave-energy propelled boat, lunar lander, hexapod, cartpole, acrobot and parallel parking. These range from 6 real-valued dimensions to 36. We show that CNMA surpasses the Nelder-Mead, Gaussian and Random Search optimization methods against the metric of number of function evaluations.

Are Perceptually-Aligned Gradients a General Property of Robust Classifiers?

For a standard convolutional neural network, optimizing over the input pixels to maximize the score of some target class will generally produce a grainy-looking version of the original image. However, Santurkar et al. (2019) demonstrated that for adversarially-trained neural networks, this optimization produces images that uncannily resemble the target class. In this paper, we show that these "perceptually-aligned gradients" also occur under randomized smoothing, an alternative means of constructing adversarially-robust classifiers. Our finding supports the hypothesis that perceptually-aligned gradients may be a general property of robust classifiers. We hope that our results will inspire research aimed at explaining this link between perceptually-aligned gradients and adversarial robustness.