Cosmology with Persistent Homology: Parameter Inference via Machine Learning

Building upon [2308.02636], this article investigates the potential constraining power of persistent homology for cosmological parameters and primordial non-Gaussianity amplitudes in a likelihood-free inference pipeline. We evaluate the ability of persistence images (PIs) to infer parameters, compared to the combined Power Spectrum and Bispectrum (PS/BS), and we compare two types of models: neural-based, and tree-based. PIs consistently lead to better predictions compared to the combined PS/BS when the parameters can be constrained (i.e., for $\{\Omega_{\rm m}, \sigma_8, n_{\rm s}, f_{\rm NL}^{\rm loc}\}$). PIs perform particularly well for $f_{\rm NL}^{\rm loc}$, showing the promise of persistent homology in constraining primordial non-Gaussianity. Our results show that combining PIs with PS/BS provides only marginal gains, indicating that the PS/BS contains little extra or complementary information to the PIs. Finally, we provide a visualization of the most important topological features for $f_{\rm NL}^{\rm loc}$ and for $\Omega_{\rm m}$. This reveals that clusters and voids (0-cycles and 2-cycles) are most informative for $\Omega_{\rm m}$, while $f_{\rm NL}^{\rm loc}$ uses the filaments (1-cycles) in addition to the other two types of topological features.

Learning from Topology: Cosmological Parameter Estimation from the Large-scale Structure

The topology of the large-scale structure of the universe contains valuable information on the underlying cosmological parameters. While persistent homology can extract this topological information, the optimal method for parameter estimation from the tool remains an open question. To address this, we propose a neural network model to map persistence images to cosmological parameters. Through a parameter recovery test, we demonstrate that our model makes accurate and precise estimates, considerably outperforming conventional Bayesian inference approaches.

From Dark Matter to Galaxies with Convolutional Neural Networks

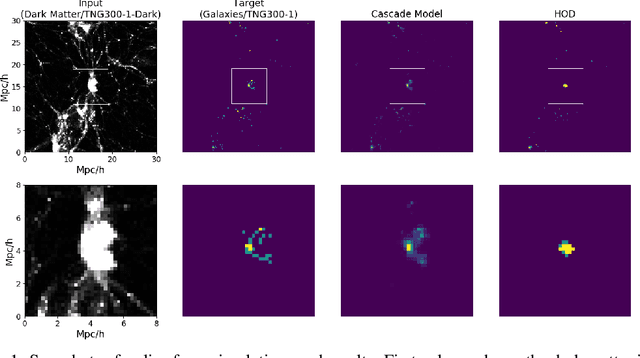
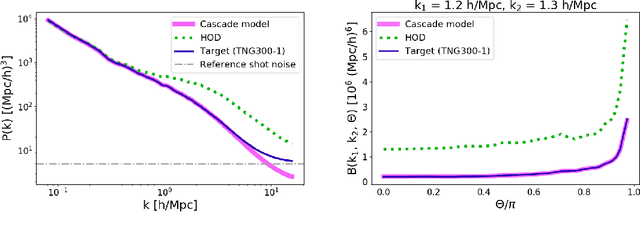
Cosmological simulations play an important role in the interpretation of astronomical data, in particular in comparing observed data to our theoretical expectations. However, to compare data with these simulations, the simulations in principle need to include gravity, magneto-hydrodyanmics, radiative transfer, etc. These ideal large-volume simulations (gravo-magneto-hydrodynamical) are incredibly computationally expensive which can cost tens of millions of CPU hours to run. In this paper, we propose a deep learning approach to map from the dark-matter-only simulation (computationally cheaper) to the galaxy distribution (from the much costlier cosmological simulation). The main challenge of this task is the high sparsity in the target galaxy distribution: space is mainly empty. We propose a cascade architecture composed of a classification filter followed by a regression procedure. We show that our result outperforms a state-of-the-art model used in the astronomical community, and provides a good trade-off between computational cost and prediction accuracy.