Foldable SuperNets: Scalable Merging of Transformers with Different Initializations and Tasks

Many recent methods aim to merge neural networks (NNs) with identical architectures trained on different tasks to obtain a single multi-task model. Most existing works tackle the simpler setup of merging NNs initialized from a common pre-trained network, where simple heuristics like weight averaging work well. This work targets a more challenging goal: merging large transformers trained on different tasks from distinct initializations. First, we demonstrate that traditional merging methods fail catastrophically in this setup. To overcome this challenge, we propose Foldable SuperNet Merge (FS-Merge), a method that optimizes a SuperNet to fuse the original models using a feature reconstruction loss. FS-Merge is simple, data-efficient, and capable of merging models of varying widths. We test FS-Merge against existing methods, including knowledge distillation, on MLPs and transformers across various settings, sizes, tasks, and modalities. FS-Merge consistently outperforms them, achieving SOTA results, particularly in limited data scenarios.

Towards Cheaper Inference in Deep Networks with Lower Bit-Width Accumulators

The majority of the research on the quantization of Deep Neural Networks (DNNs) is focused on reducing the precision of tensors visible by high-level frameworks (e.g., weights, activations, and gradients). However, current hardware still relies on high-accuracy core operations. Most significant is the operation of accumulating products. This high-precision accumulation operation is gradually becoming the main computational bottleneck. This is because, so far, the usage of low-precision accumulators led to a significant degradation in performance. In this work, we present a simple method to train and fine-tune high-end DNNs, to allow, for the first time, utilization of cheaper, $12$-bits accumulators, with no significant degradation in accuracy. Lastly, we show that as we decrease the accumulation precision further, using fine-grained gradient approximations can improve the DNN accuracy.

Optimal Fine-Grained N:M sparsity for Activations and Neural Gradients

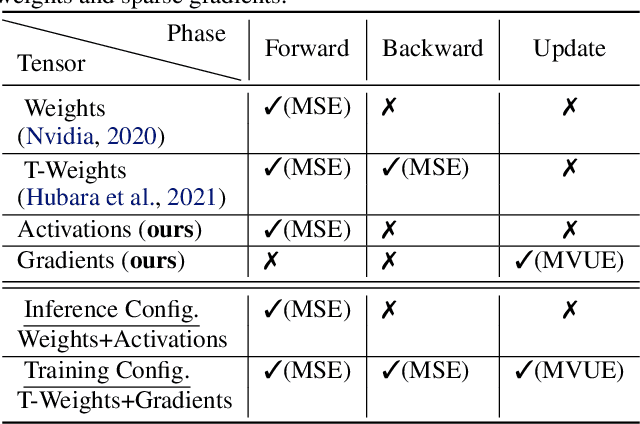
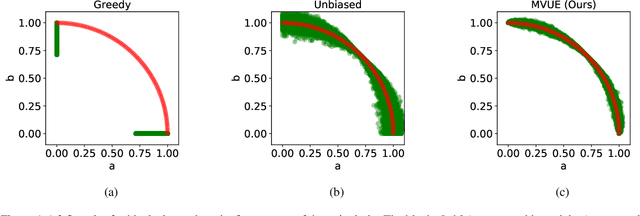
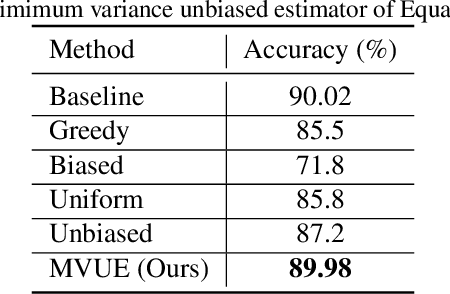
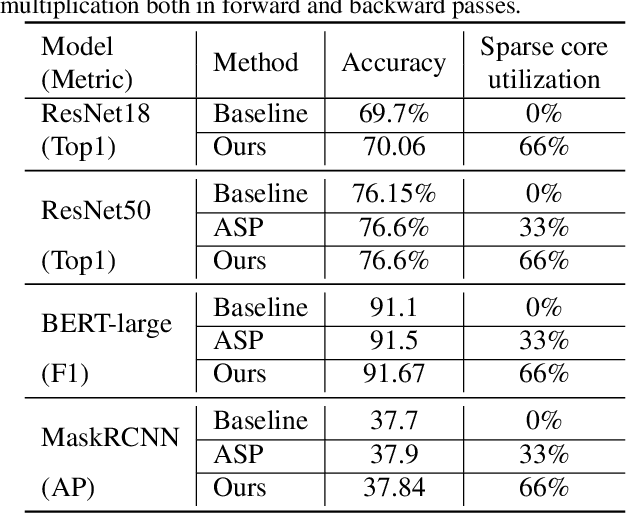
In deep learning, fine-grained N:M sparsity reduces the data footprint and bandwidth of a General Matrix multiply (GEMM) by x2, and doubles throughput by skipping computation of zero values. So far, it was only used to prune weights. We examine how this method can be used also for activations and their gradients (i.e., "neural gradients"). To this end, we first establish tensor-level optimality criteria. Previous works aimed to minimize the mean-square-error (MSE) of each pruned block. We show that while minimization of the MSE works fine for pruning the activations, it catastrophically fails for the neural gradients. Instead, we show that optimal pruning of the neural gradients requires an unbiased minimum-variance pruning mask. We design such specialized masks, and find that in most cases, 1:2 sparsity is sufficient for training, and 2:4 sparsity is usually enough when this is not the case. Further, we suggest combining several such methods together in order to speed up training even more. A reference implementation is supplied in https://github.com/brianchmiel/Act-and-Grad-structured-sparsity.

Accelerated Sparse Neural Training: A Provable and Efficient Method to Find N:M Transposable Masks

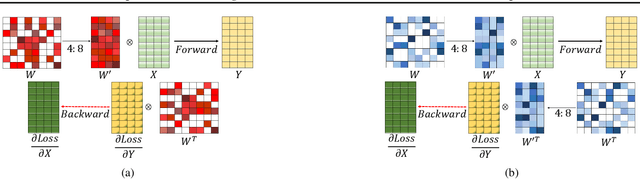
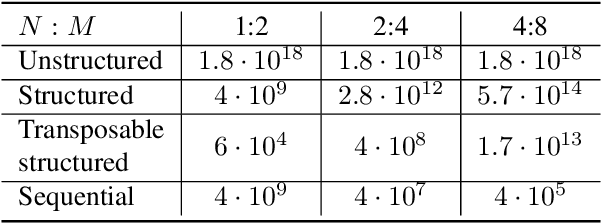
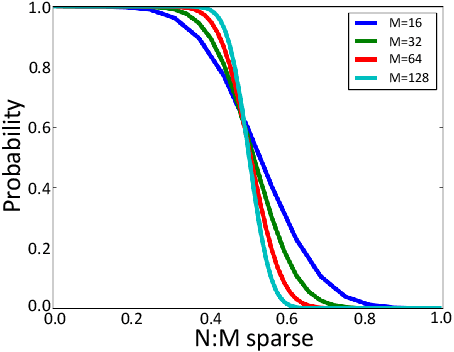
Recently, researchers proposed pruning deep neural network weights (DNNs) using an $N:M$ fine-grained block sparsity mask. In this mask, for each block of $M$ weights, we have at least $N$ zeros. In contrast to unstructured sparsity, $N:M$ fine-grained block sparsity allows acceleration in actual modern hardware. So far, this was used for DNN acceleration at the inference phase. First, we suggest a method to convert a pretrained model with unstructured sparsity to a $N:M$ fine-grained block sparsity model, with little to no training. Then, to also allow such acceleration in the training phase, we suggest a novel transposable-fine-grained sparsity mask where the same mask can be used for both forward and backward passes. Our transposable mask ensures that both the weight matrix and its transpose follow the same sparsity pattern; thus the matrix multiplication required for passing the error backward can also be accelerated. We discuss the transposable constraint and devise a new measure for mask constraints, called mask-diversity (MD), which correlates with their expected accuracy. Then, we formulate the problem of finding the optimal transposable mask as a minimum-cost-flow problem and suggest a fast linear approximation that can be used when the masks dynamically change while training. Our experiments suggest 2x speed-up with no accuracy degradation over vision and language models. A reference implementation can be found at https://github.com/papers-submission/structured_transposable_masks.

Improving Post Training Neural Quantization: Layer-wise Calibration and Integer Programming

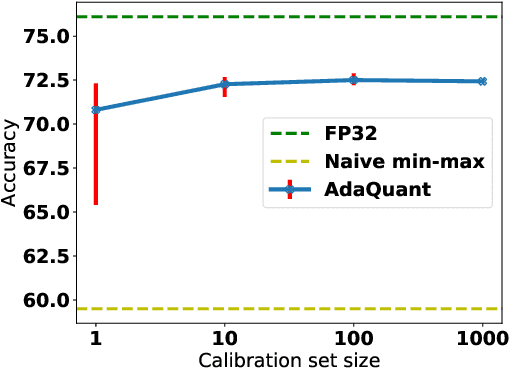
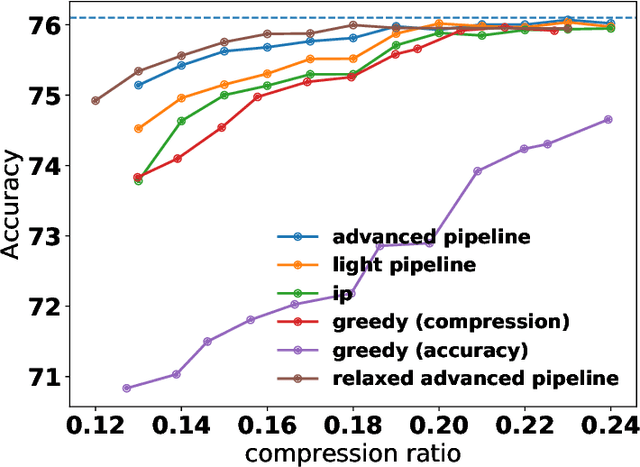
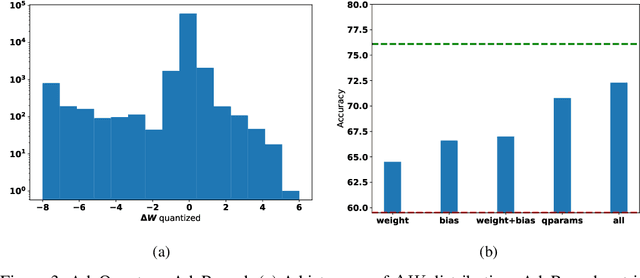
Most of the literature on neural network quantization requires some training of the quantized model (fine-tuning). However, this training is not always possible in real-world scenarios, as it requires the full dataset. Lately, post-training quantization methods have gained considerable attention, as they are simple to use and require only a small, unlabeled calibration set. Yet, they usually incur significant accuracy degradation when quantized below 8-bits. This paper seeks to address this problem by introducing two pipelines, advanced and light, where the former involves: (i) minimizing the quantization errors of each layer by optimizing its parameters over the calibration set; (ii) using integer programming to optimally allocate the desired bit-width for each layer while constraining accuracy degradation or model compression; and (iii) tuning the mixed-precision model statistics to correct biases introduced during quantization. While the light pipeline which invokes only (ii) and (iii) obtains surprisingly accurate results; the advanced pipeline yields state-of-the-art accuracy-compression ratios for both vision and text models. For instance, on ResNet50, we obtain less than 1% accuracy degradation while compressing the model to 13% of its original size. We open-sourced our code.

The Knowledge Within: Methods for Data-Free Model Compression

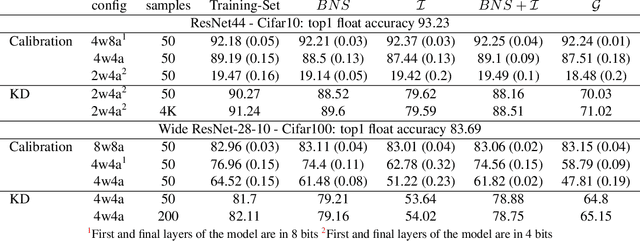
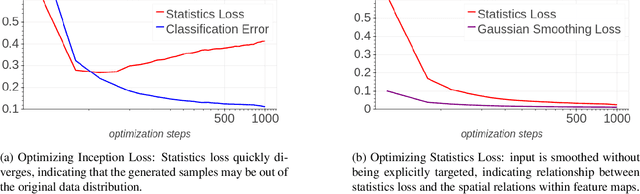
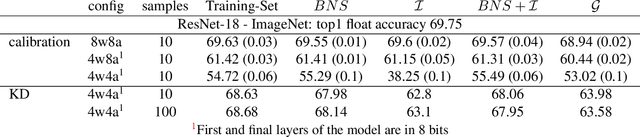
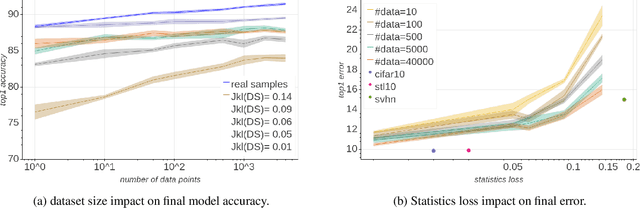
Background: Recently, an extensive amount of research has been focused on compressing and accelerating Deep Neural Networks (DNNs). So far, high compression rate algorithms required the entire training dataset, or its subset, for fine-tuning and low precision calibration process. However, this requirement is unacceptable when sensitive data is involved as in medical and biometric use-cases. Contributions: We present three methods for generating synthetic samples from trained models. Then, we demonstrate how these samples can be used to fine-tune or to calibrate quantized models with negligible accuracy degradation compared to the original training set --- without using any real data in the process. Furthermore, we suggest that our best performing method, leveraging intrinsic batch normalization layers' statistics of a trained model, can be used to evaluate data similarity. Our approach opens a path towards genuine data-free model compression, alleviating the need for training data during deployment.

MLPerf Inference Benchmark

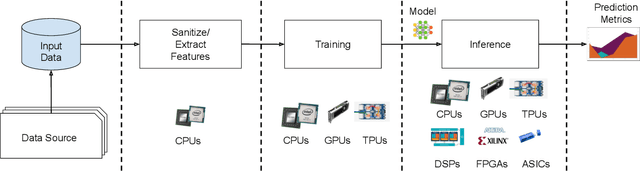
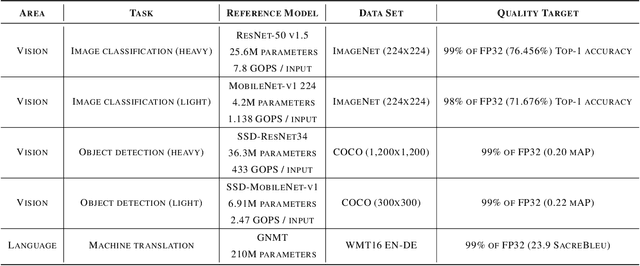
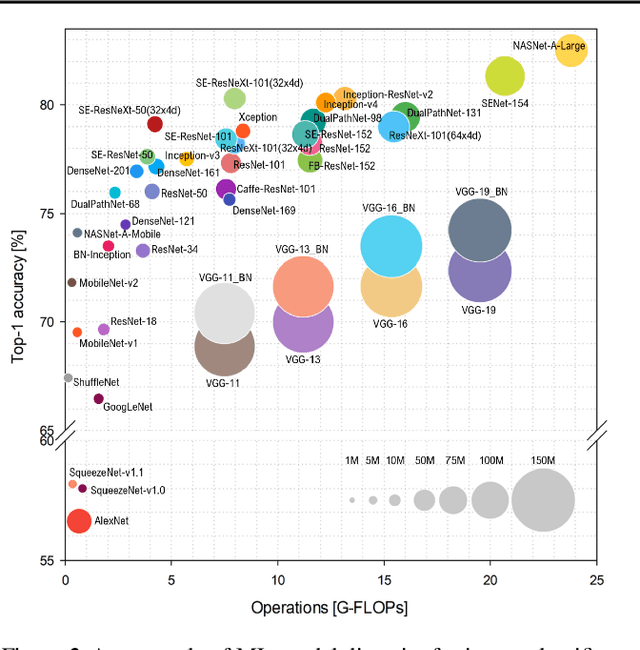
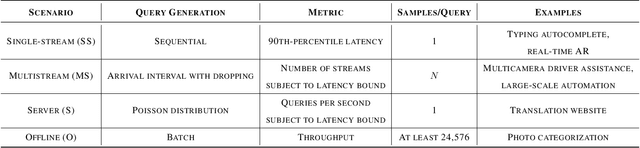
Machine-learning (ML) hardware and software system demand is burgeoning. Driven by ML applications, the number of different ML inference systems has exploded. Over 100 organizations are building ML inference chips, and the systems that incorporate existing models span at least three orders of magnitude in power consumption and four orders of magnitude in performance; they range from embedded devices to data-center solutions. Fueling the hardware are a dozen or more software frameworks and libraries. The myriad combinations of ML hardware and ML software make assessing ML-system performance in an architecture-neutral, representative, and reproducible manner challenging. There is a clear need for industry-wide standard ML benchmarking and evaluation criteria. MLPerf Inference answers that call. Driven by more than 30 organizations as well as more than 200 ML engineers and practitioners, MLPerf implements a set of rules and practices to ensure comparability across systems with wildly differing architectures. In this paper, we present the method and design principles of the initial MLPerf Inference release. The first call for submissions garnered more than 600 inference-performance measurements from 14 organizations, representing over 30 systems that show a range of capabilities.

Mix & Match: training convnets with mixed image sizes for improved accuracy, speed and scale resiliency

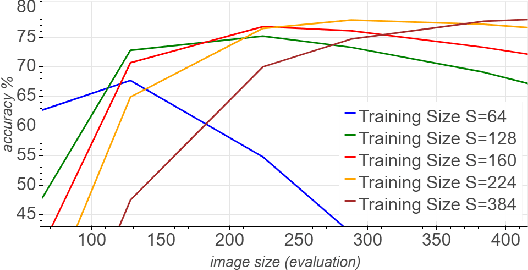
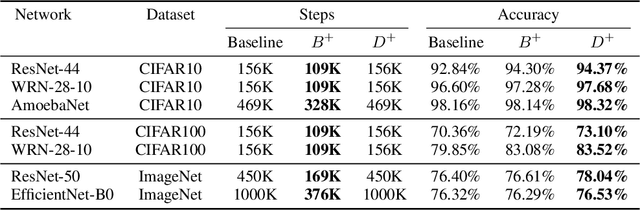
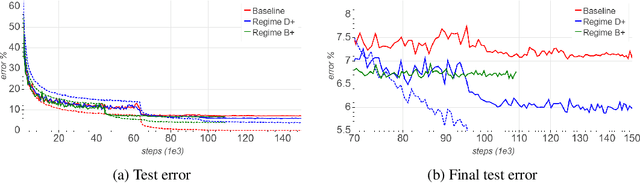
Convolutional neural networks (CNNs) are commonly trained using a fixed spatial image size predetermined for a given model. Although trained on images of aspecific size, it is well established that CNNs can be used to evaluate a wide range of image sizes at test time, by adjusting the size of intermediate feature maps. In this work, we describe and evaluate a novel mixed-size training regime that mixes several image sizes at training time. We demonstrate that models trained using our method are more resilient to image size changes and generalize well even on small images. This allows faster inference by using smaller images attest time. For instance, we receive a 76.43% top-1 accuracy using ResNet50 with an image size of 160, which matches the accuracy of the baseline model with 2x fewer computations. Furthermore, for a given image size used at test time, we show this method can be exploited either to accelerate training or the final test accuracy. For example, we are able to reach a 79.27% accuracy with a model evaluated at a 288 spatial size for a relative improvement of 14% over the baseline.

Augment your batch: better training with larger batches

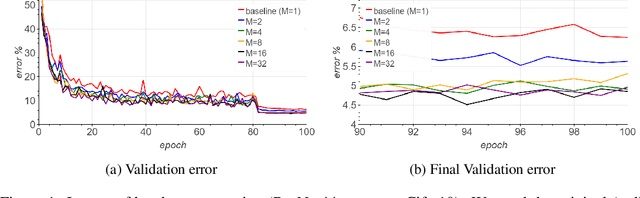
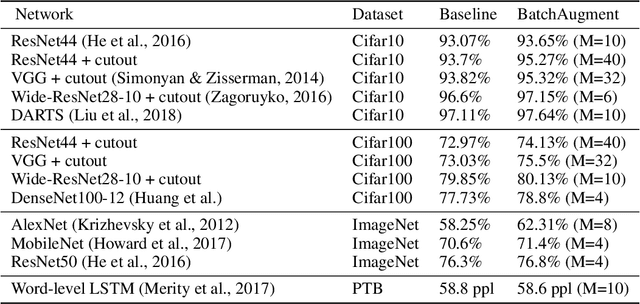
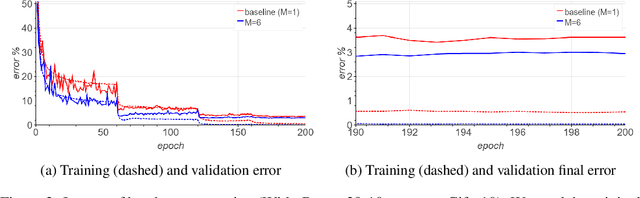
Large-batch SGD is important for scaling training of deep neural networks. However, without fine-tuning hyperparameter schedules, the generalization of the model may be hampered. We propose to use batch augmentation: replicating instances of samples within the same batch with different data augmentations. Batch augmentation acts as a regularizer and an accelerator, increasing both generalization and performance scaling. We analyze the effect of batch augmentation on gradient variance and show that it empirically improves convergence for a wide variety of deep neural networks and datasets. Our results show that batch augmentation reduces the number of necessary SGD updates to achieve the same accuracy as the state-of-the-art. Overall, this simple yet effective method enables faster training and better generalization by allowing more computational resources to be used concurrently.

Scalable Methods for 8-bit Training of Neural Networks

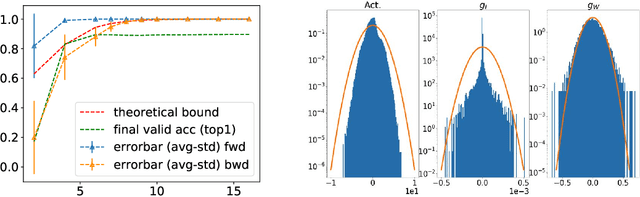
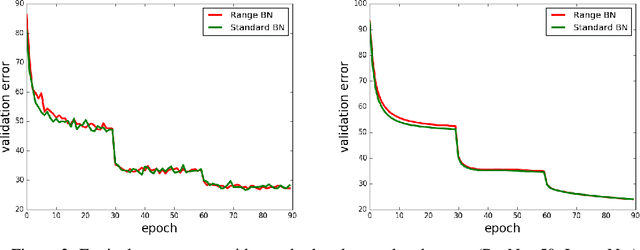
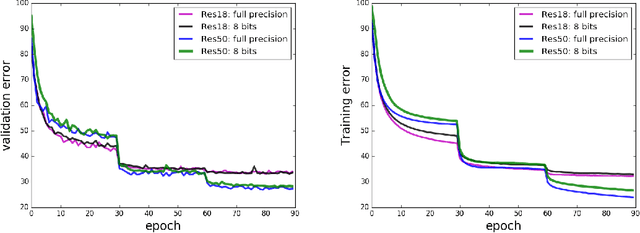
Quantized Neural Networks (QNNs) are often used to improve network efficiency during the inference phase, i.e. after the network has been trained. Extensive research in the field suggests many different quantization schemes. Still, the number of bits required, as well as the best quantization scheme, are yet unknown. Our theoretical analysis suggests that most of the training process is robust to substantial precision reduction, and points to only a few specific operations that require higher precision. Armed with this knowledge, we quantize the model parameters, activations and layer gradients to 8-bit, leaving at a higher precision only the final step in the computation of the weight gradients. Additionally, as QNNs require batch-normalization to be trained at high precision, we introduce Range Batch-Normalization (BN) which has significantly higher tolerance to quantization noise and improved computational complexity. Our simulations show that Range BN is equivalent to the traditional batch norm if a precise scale adjustment, which can be approximated analytically, is applied. To the best of the authors' knowledge, this work is the first to quantize the weights, activations, as well as a substantial volume of the gradients stream, in all layers (including batch normalization) to 8-bit while showing state-of-the-art results over the ImageNet-1K dataset.