Francisco Barahona
Logical Credal Networks
Sep 25, 2021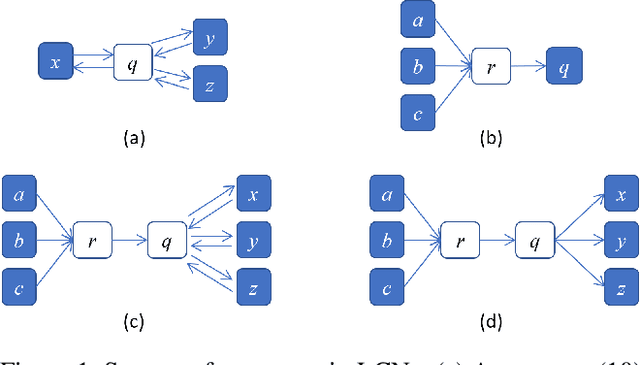
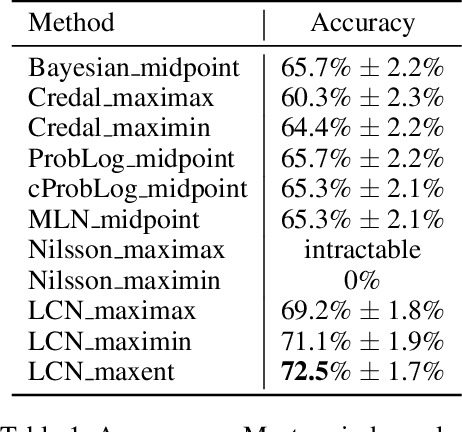
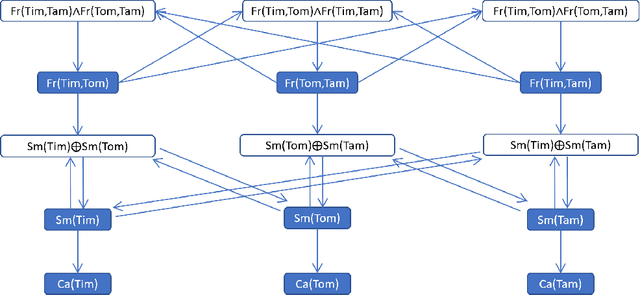
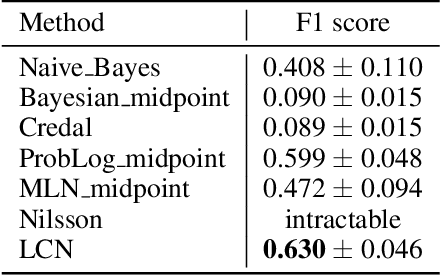
Abstract:This paper introduces Logical Credal Networks, an expressive probabilistic logic that generalizes many prior models that combine logic and probability. Given imprecise information represented by probability bounds and conditional probability bounds of logic formulas, this logic specifies a set of probability distributions over all interpretations. On the one hand, our approach allows propositional and first-order logic formulas with few restrictions, e.g., without requiring acyclicity. On the other hand, it has a Markov condition similar to Bayesian networks and Markov random fields that is critical in real-world applications. Having both these properties makes this logic unique, and we investigate its performance on maximum a posteriori inference tasks, including solving Mastermind games with uncertainty and detecting credit card fraud. The results show that the proposed method outperforms existing approaches, and its advantage lies in aggregating multiple sources of imprecise information.
Logical Neural Networks
Jun 23, 2020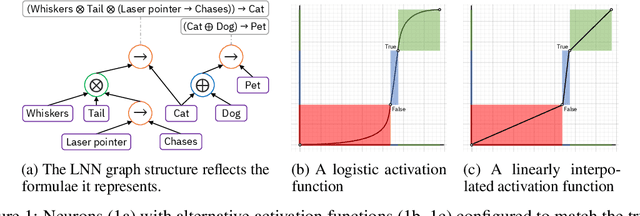

Abstract:We propose a novel framework seamlessly providing key properties of both neural nets (learning) and symbolic logic (knowledge and reasoning). Every neuron has a meaning as a component of a formula in a weighted real-valued logic, yielding a highly intepretable disentangled representation. Inference is omnidirectional rather than focused on predefined target variables, and corresponds to logical reasoning, including classical first-order logic theorem proving as a special case. The model is end-to-end differentiable, and learning minimizes a novel loss function capturing logical contradiction, yielding resilience to inconsistent knowledge. It also enables the open-world assumption by maintaining bounds on truth values which can have probabilistic semantics, yielding resilience to incomplete knowledge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge