Ronald Fagin
A Framework for Combining Entity Resolution and Query Answering in Knowledge Bases
Mar 13, 2023Abstract:We propose a new framework for combining entity resolution and query answering in knowledge bases (KBs) with tuple-generating dependencies (tgds) and equality-generating dependencies (egds) as rules. We define the semantics of the KB in terms of special instances that involve equivalence classes of entities and sets of values. Intuitively, the former collect all entities denoting the same real-world object, while the latter collect all alternative values for an attribute. This approach allows us to both resolve entities and bypass possible inconsistencies in the data. We then design a chase procedure that is tailored to this new framework and has the feature that it never fails; moreover, when the chase procedure terminates, it produces a universal solution, which in turn can be used to obtain the certain answers to conjunctive queries. We finally discuss challenges arising when the chase does not terminate.
Foundations of Reasoning with Uncertainty via Real-valued Logics
Aug 06, 2020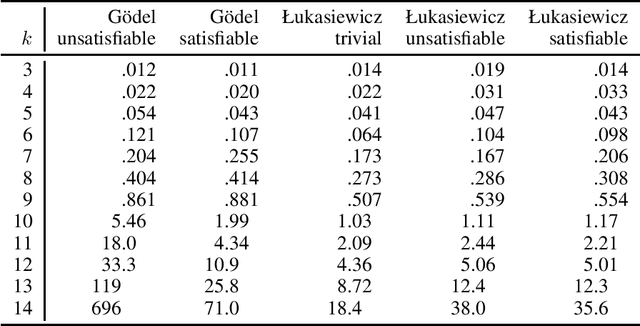
Abstract:Real-valued logics underlie an increasing number of neuro-symbolic approaches, though typically their logical inference capabilities are characterized only qualitatively. We provide foundations for establishing the correctness and power of such systems. For the first time, we give a sound and complete axiomatization for a broad class containing all the common real-valued logics. This axiomatization allows us to derive exactly what information can be inferred about the combinations of real values of a collection of formulas given information about the combinations of real values of several other collections of formulas. We then extend the axiomatization to deal with weighted subformulas. Finally, we give a decision procedure based on linear programming for deciding, under certain natural assumptions, whether a set of our sentences logically implies another of our sentences.
Logical Neural Networks
Jun 23, 2020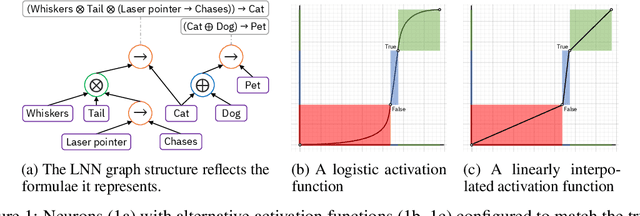

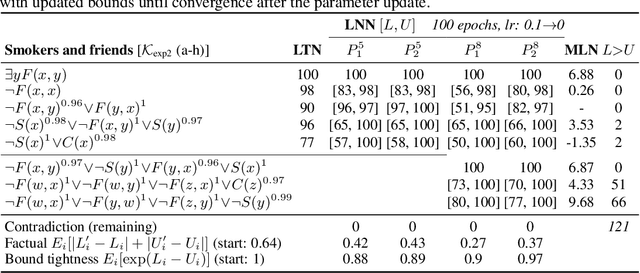
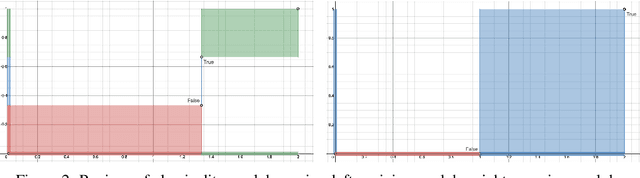
Abstract:We propose a novel framework seamlessly providing key properties of both neural nets (learning) and symbolic logic (knowledge and reasoning). Every neuron has a meaning as a component of a formula in a weighted real-valued logic, yielding a highly intepretable disentangled representation. Inference is omnidirectional rather than focused on predefined target variables, and corresponds to logical reasoning, including classical first-order logic theorem proving as a special case. The model is end-to-end differentiable, and learning minimizes a novel loss function capturing logical contradiction, yielding resilience to inconsistent knowledge. It also enables the open-world assumption by maintaining bounds on truth values which can have probabilistic semantics, yielding resilience to incomplete knowledge.
A New Approach to Updating Beliefs
Mar 27, 2013Abstract:We define a new notion of conditional belief, which plays the same role for Dempster-Shafer belief functions as conditional probability does for probability functions. Our definition is different from the standard definition given by Dempster, and avoids many of the well-known problems of that definition. Just as the conditional probability Pr (lB) is a probability function which is the result of conditioning on B being true, so too our conditional belief function Bel (lB) is a belief function which is the result of conditioning on B being true. We define the conditional belief as the lower envelope (that is, the inf) of a family of conditional probability functions, and provide a closed form expression for it. An alternate way of understanding our definition of conditional belief is provided by considering ideas from an earlier paper [Fagin and Halpern, 1989], where we connect belief functions with inner measures. In particular, we show here how to extend the definition of conditional probability to non measurable sets, in order to get notions of inner and outer conditional probabilities, which can be viewed as best approximations to the true conditional probability, given our lack of information. Our definition of conditional belief turns out to be an exact analogue of our definition of inner conditional probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge