Ishanu Chattopadhyay
Emergenet: A Digital Twin of Sequence Evolution for Scalable Emergence Risk Assessment of Animal Influenza A Strains
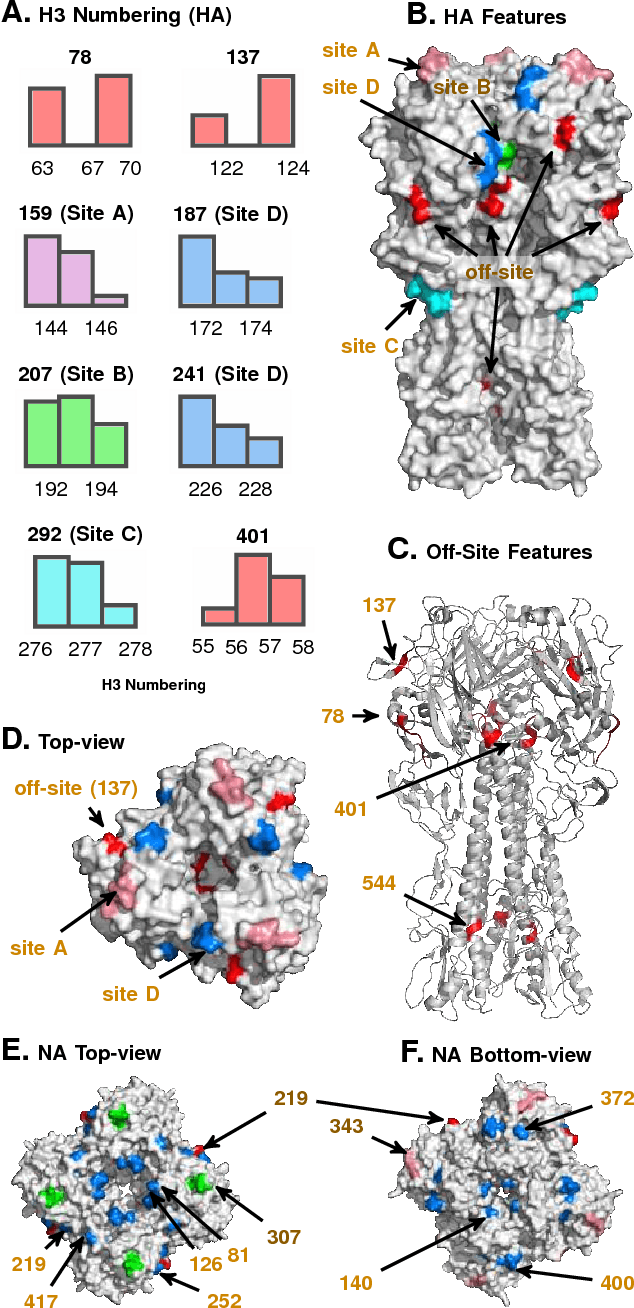
Nov 26, 2024Abstract:Despite having triggered devastating pandemics in the past, our ability to quantitatively assess the emergence potential of individual strains of animal influenza viruses remains limited. This study introduces Emergenet, a tool to infer a digital twin of sequence evolution to chart how new variants might emerge in the wild. Our predictions based on Emergenets built only using 220,151 Hemagglutinnin (HA) sequences consistently outperform WHO seasonal vaccine recommendations for H1N1/H3N2 subtypes over two decades (average match-improvement: 3.73 AAs, 28.40\%), and are at par with state-of-the-art approaches that use more detailed phenotypic annotations. Finally, our generative models are used to scalably calculate the current odds of emergence of animal strains not yet in human circulation, which strongly correlates with CDC's expert-assessed Influenza Risk Assessment Tool (IRAT) scores (Pearson's $r = 0.721, p = 10^{-4}$). A minimum five orders of magnitude speedup over CDC's assessment (seconds vs months) then enabled us to analyze 6,354 animal strains collected post-2020 to identify 35 strains with high emergence scores ($> 7.7$). The Emergenet framework opens the door to preemptive pandemic mitigation through targeted inoculation of animal hosts before the first human infection.
Long-range Event-level Prediction and Response Simulation for Urban Crime and Global Terrorism with Granger Networks
Nov 04, 2019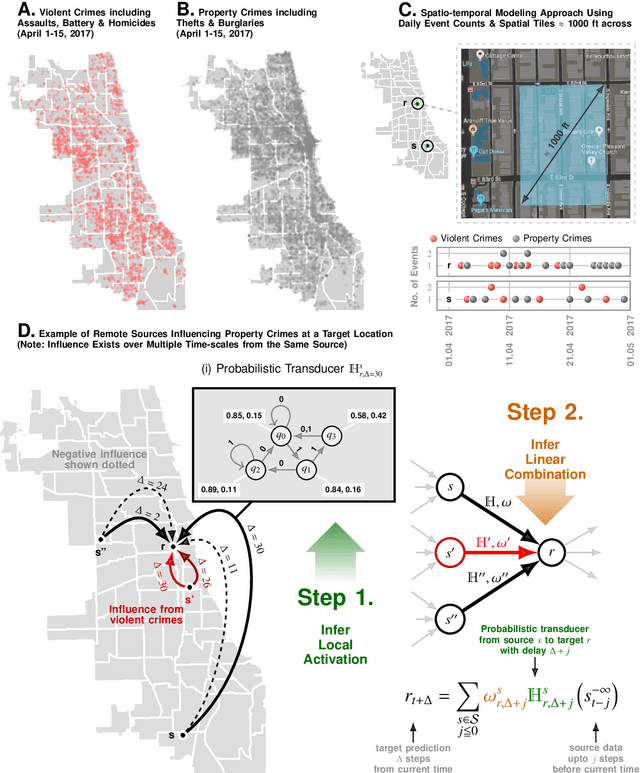
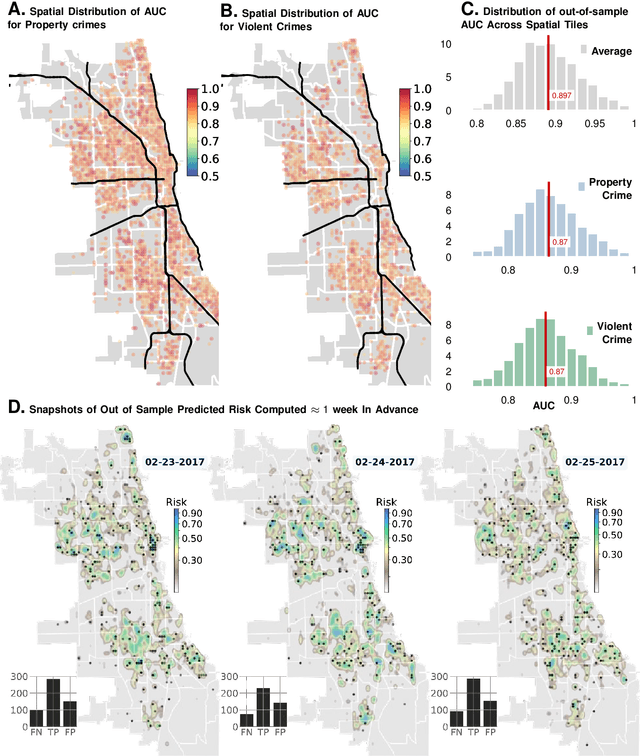
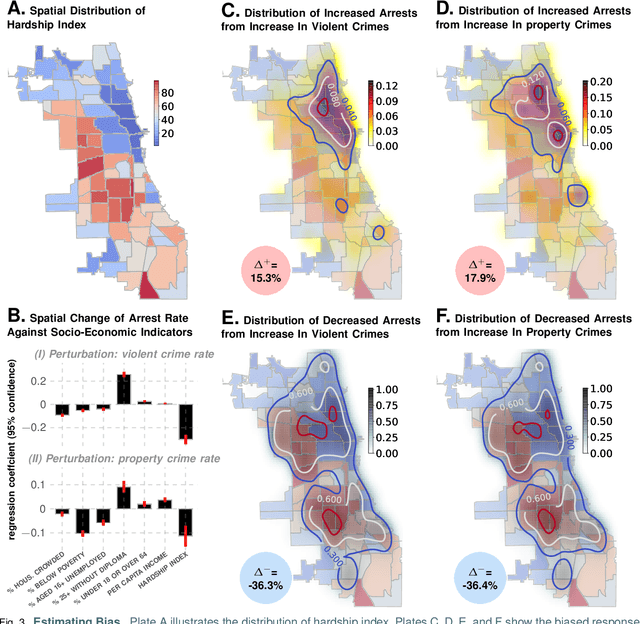
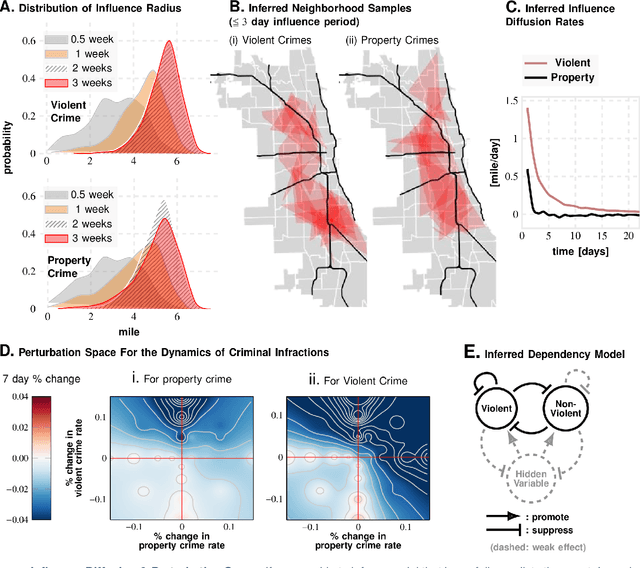
Abstract:Large-scale trends in urban crime and global terrorism are well-predicted by socio-economic drivers, but focused, event-level predictions have had limited success. Standard machine learning approaches are promising, but lack interpretability, are generally interpolative, and ineffective for precise future interventions with costly and wasteful false positives. Here, we are introducing Granger Network inference as a new forecasting approach for individual infractions with demonstrated performance far surpassing past results, yet transparent enough to validate and extend social theory. Considering the problem of predicting crime in the City of Chicago, we achieve an average AUC of ~90\% for events predicted a week in advance within spatial tiles approximately $1000$ ft across. Instead of pre-supposing that crimes unfold across contiguous spaces akin to diffusive systems, we learn the local transport rules from data. As our key insights, we uncover indications of suburban bias -- how law-enforcement response is modulated by socio-economic contexts with disproportionately negative impacts in the inner city -- and how the dynamics of violent and property crimes co-evolve and constrain each other -- lending quantitative support to controversial pro-active policing policies. To demonstrate broad applicability to spatio-temporal phenomena, we analyze terror attacks in the middle-east in the recent past, and achieve an AUC of ~80% for predictions made a week in advance, and within spatial tiles measuring approximately 120 miles across. We conclude that while crime operates near an equilibrium quickly dissipating perturbations, terrorism does not. Indeed terrorism aims to destabilize social order, as shown by its dynamics being susceptible to run-away increases in event rates under small perturbations.
Data Smashing 2.0: Sequence Likelihood (SL) Divergence For Fast Time Series Comparison
Oct 08, 2019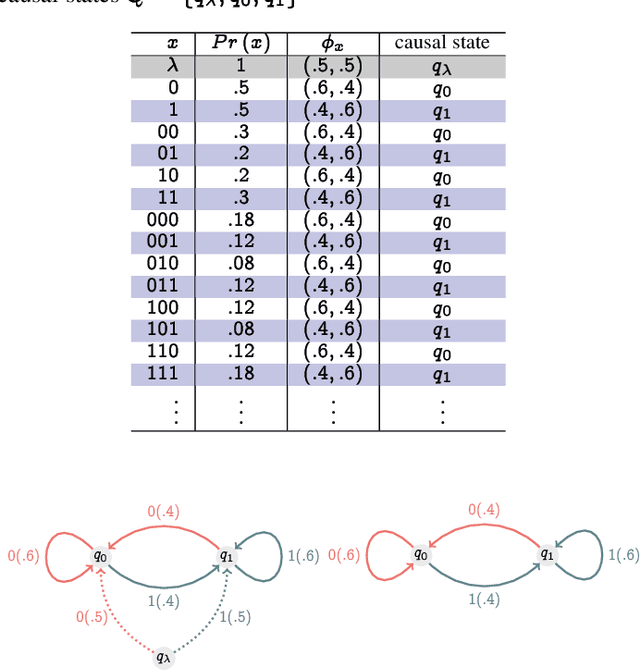
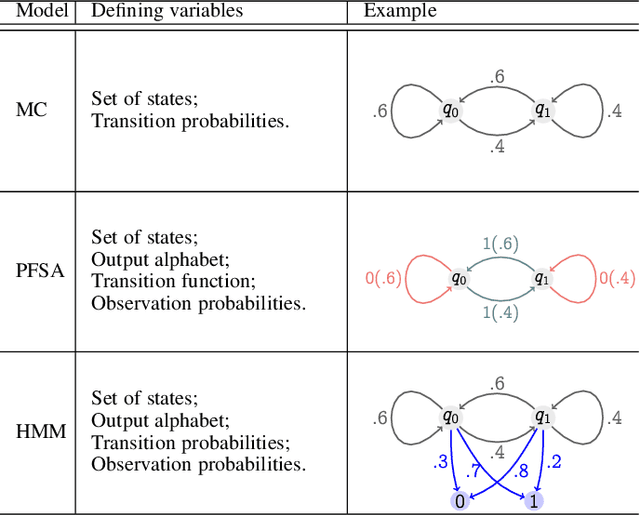
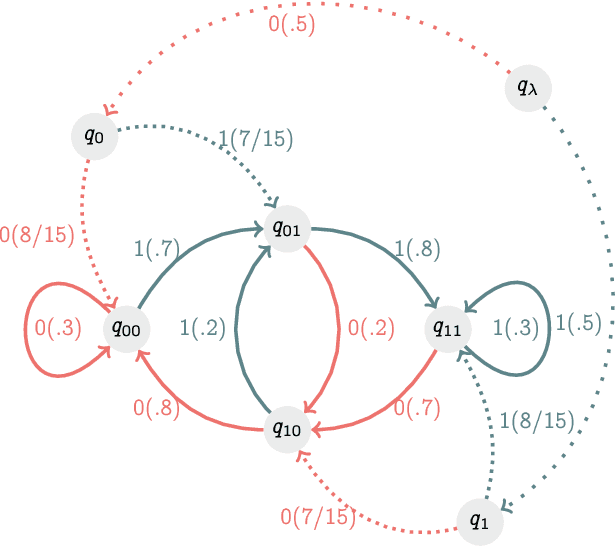
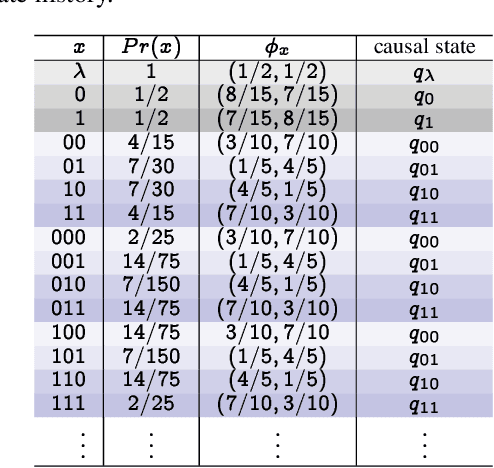
Abstract:Recognizing subtle historical patterns is central to modeling and forecasting problems in time series analysis. Here we introduce and develop a new approach to quantify deviations in the underlying hidden generators of observed data streams, resulting in a new efficiently computable universal metric for time series. The proposed metric is in the sense that we can compare and contrast data streams regardless of where and how they are generated and without any feature engineering step. The approach proposed in this paper is conceptually distinct from our previous work on data smashing, and vastly improves discrimination performance and computing speed. The core idea here is the generalization of the notion of KL divergence often used to compare probability distributions to a notion of divergence in time series. We call this the sequence likelihood (SL) divergence, which may be used to measure deviations within a well-defined class of discrete-valued stochastic processes. We devise efficient estimators of SL divergence from finite sample paths and subsequently formulate a universal metric useful for computing distance between time series produced by hidden stochastic generators.
A Tamper-Free Semi-Universal Communication System for Deletion Channels
Apr 09, 2018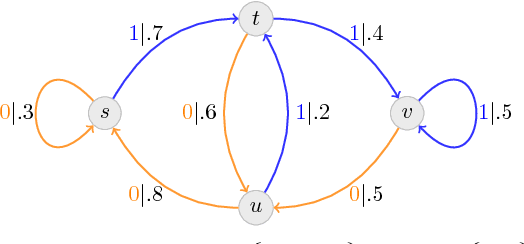
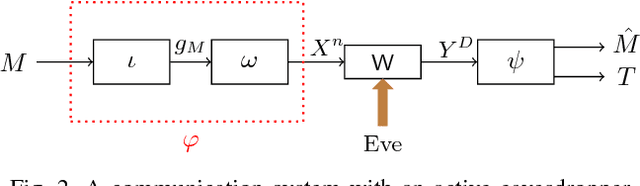
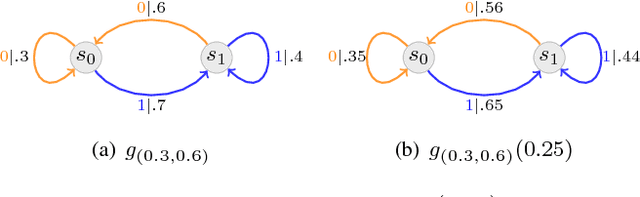
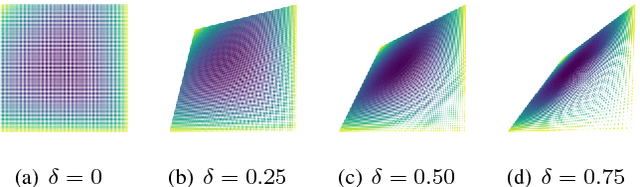
Abstract:We investigate the problem of reliable communication between two legitimate parties over deletion channels under an active eavesdropping (aka jamming) adversarial model. To this goal, we develop a theoretical framework based on probabilistic finite-state automata to define novel encoding and decoding schemes that ensure small error probability in both message decoding as well as tamper detecting. We then experimentally verify the reliability and tamper-detection property of our scheme.
Autostacker: A Compositional Evolutionary Learning System
Mar 02, 2018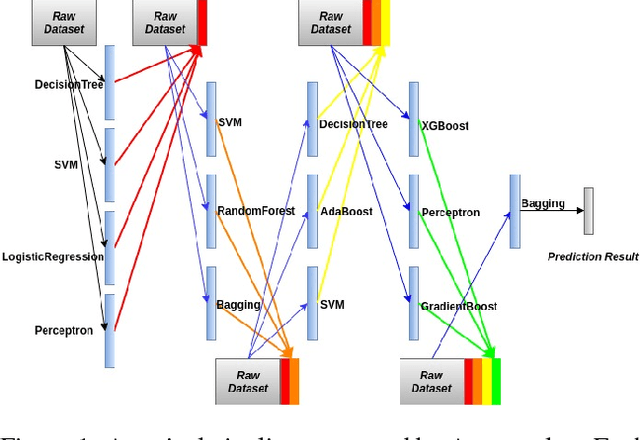
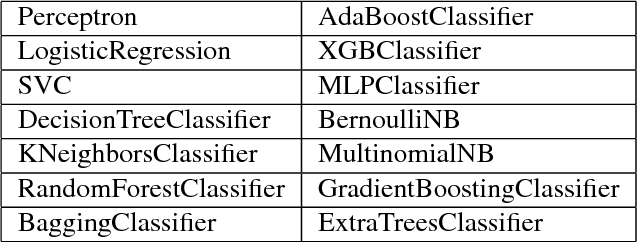

Abstract:We introduce an automatic machine learning (AutoML) modeling architecture called Autostacker, which combines an innovative hierarchical stacking architecture and an Evolutionary Algorithm (EA) to perform efficient parameter search. Neither prior domain knowledge about the data nor feature preprocessing is needed. Using EA, Autostacker quickly evolves candidate pipelines with high predictive accuracy. These pipelines can be used as is or as a starting point for human experts to build on. Autostacker finds innovative combinations and structures of machine learning models, rather than selecting a single model and optimizing its hyperparameters. Compared with other AutoML systems on fifteen datasets, Autostacker achieves state-of-art or competitive performance both in terms of test accuracy and time cost.
A Hilbert Space of Stationary Ergodic Processes
Jan 25, 2018
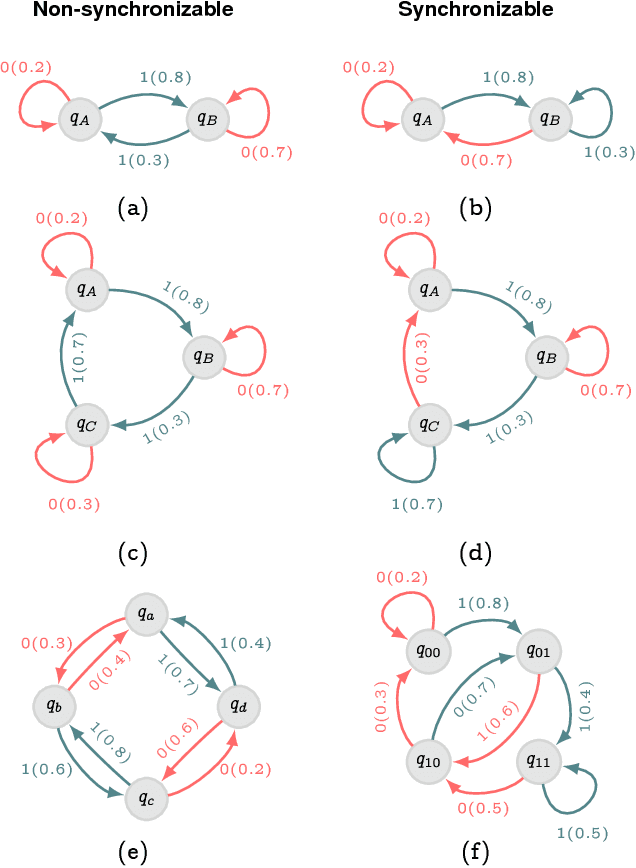
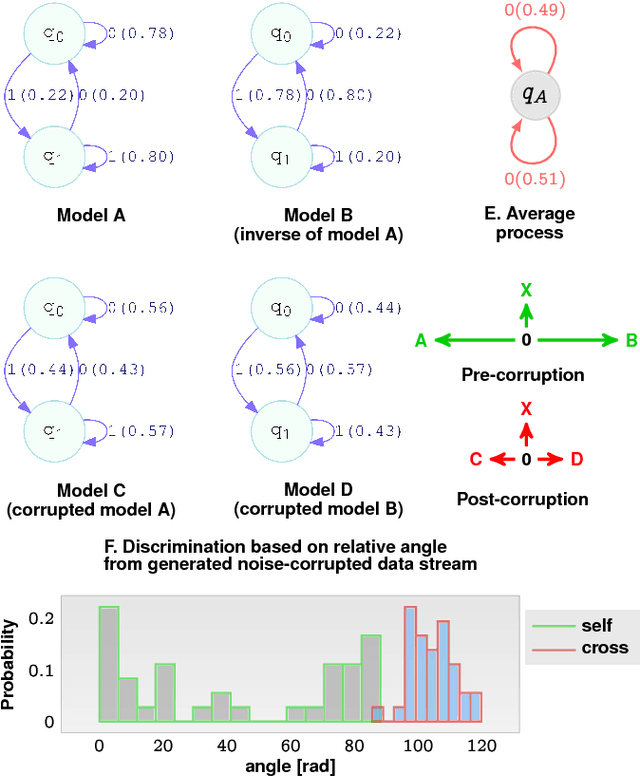
Abstract:Identifying meaningful signal buried in noise is a problem of interest arising in diverse scenarios of data-driven modeling. We present here a theoretical framework for exploiting intrinsic geometry in data that resists noise corruption, and might be identifiable under severe obfuscation. Our approach is based on uncovering a valid complete inner product on the space of ergodic stationary finite valued processes, providing the latter with the structure of a Hilbert space on the real field. This rigorous construction, based on non-standard generalizations of the notions of sum and scalar multiplication of finite dimensional probability vectors, allows us to meaningfully talk about "angles" between data streams and data sources, and, make precise the notion of orthogonal stochastic processes. In particular, the relative angles appear to be preserved, and identifiable, under severe noise, and will be developed in future as the underlying principle for robust classification, clustering and unsupervised featurization algorithms.
Algorithmic Bio-surveillance For Precise Spatio-temporal Prediction of Zoonotic Emergence
Jan 23, 2018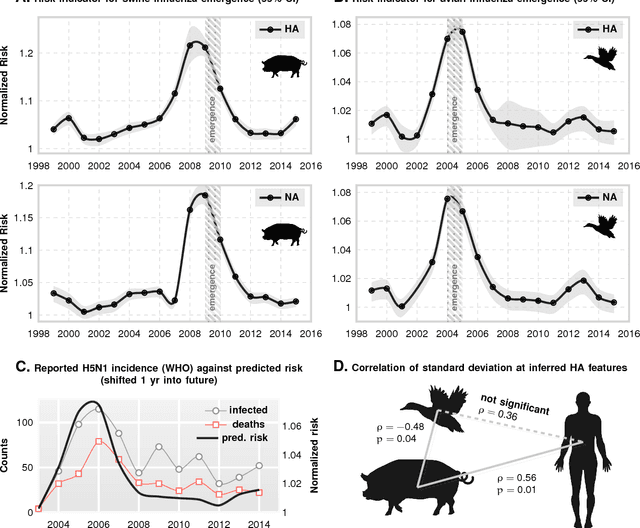
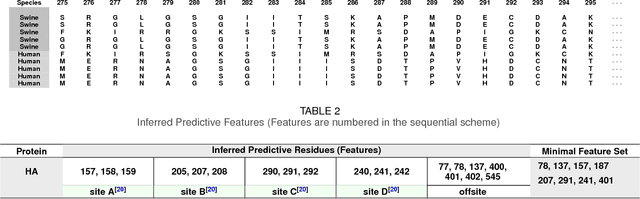

Abstract:Viral zoonoses have emerged as the key drivers of recent pandemics. Human infection by zoonotic viruses are either spillover events -- isolated infections that fail to cause a widespread contagion -- or species jumps, where successful adaptation to the new host leads to a pandemic. Despite expensive bio-surveillance efforts, historically emergence response has been reactive, and post-hoc. Here we use machine inference to demonstrate a high accuracy predictive bio-surveillance capability, designed to pro-actively localize an impending species jump via automated interrogation of massive sequence databases of viral proteins. Our results suggest that a jump might not purely be the result of an isolated unfortunate cross-infection localized in space and time; there are subtle yet detectable patterns of genotypic changes accumulating in the global viral population leading up to emergence. Using tens of thousands of protein sequences simultaneously, we train models that track maximum achievable accuracy for disambiguating host tropism from the primary structure of surface proteins, and show that the inverse classification accuracy is a quantitative indicator of jump risk. We validate our claim in the context of the 2009 swine flu outbreak, and the 2004 emergence of H5N1 subspecies of Influenza A from avian reservoirs; illustrating that interrogation of the global viral population can unambiguously track a near monotonic risk elevation over several preceding years leading to eventual emergence.
Causality Networks
Jun 25, 2014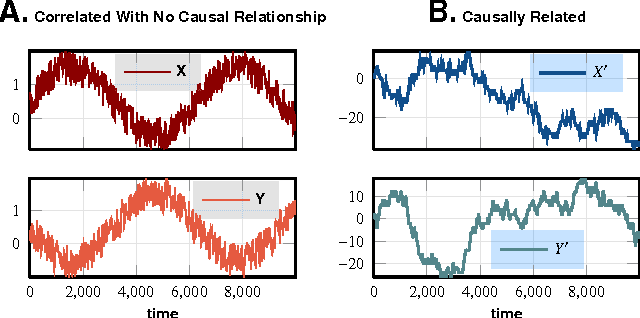

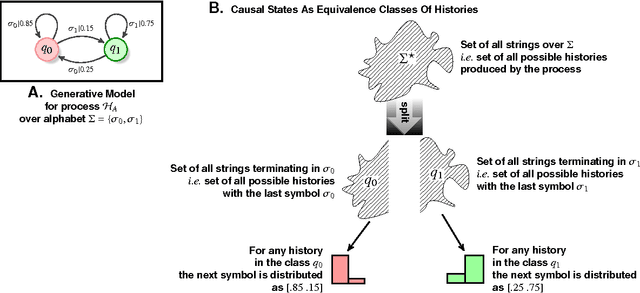
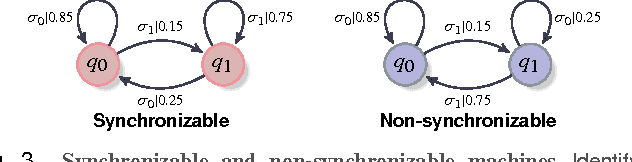
Abstract:While correlation measures are used to discern statistical relationships between observed variables in almost all branches of data-driven scientific inquiry, what we are really interested in is the existence of causal dependence. Designing an efficient causality test, that may be carried out in the absence of restrictive pre-suppositions on the underlying dynamical structure of the data at hand, is non-trivial. Nevertheless, ability to computationally infer statistical prima facie evidence of causal dependence may yield a far more discriminative tool for data analysis compared to the calculation of simple correlations. In the present work, we present a new non-parametric test of Granger causality for quantized or symbolic data streams generated by ergodic stationary sources. In contrast to state-of-art binary tests, our approach makes precise and computes the degree of causal dependence between data streams, without making any restrictive assumptions, linearity or otherwise. Additionally, without any a priori imposition of specific dynamical structure, we infer explicit generative models of causal cross-dependence, which may be then used for prediction. These explicit models are represented as generalized probabilistic automata, referred to crossed automata, and are shown to be sufficient to capture a fairly general class of causal dependence. The proposed algorithms are computationally efficient in the PAC sense; $i.e.$, we find good models of cross-dependence with high probability, with polynomial run-times and sample complexities. The theoretical results are applied to weekly search-frequency data from Google Trends API for a chosen set of socially "charged" keywords. The causality network inferred from this dataset reveals, quite expectedly, the causal importance of certain keywords. It is also illustrated that correlation analysis fails to gather such insight.
Computing Entropy Rate Of Symbol Sources & A Distribution-free Limit Theorem
Mar 21, 2014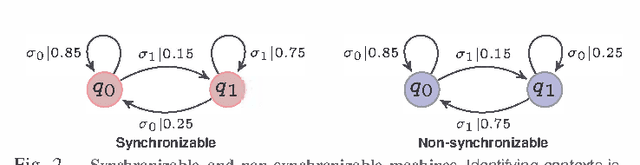
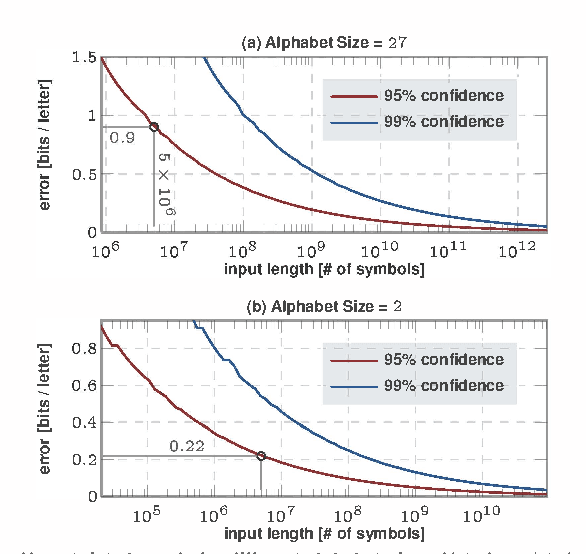
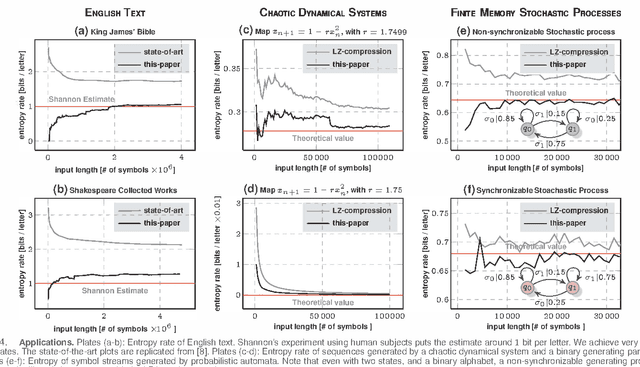

Abstract:Entropy rate of sequential data-streams naturally quantifies the complexity of the generative process. Thus entropy rate fluctuations could be used as a tool to recognize dynamical perturbations in signal sources, and could potentially be carried out without explicit background noise characterization. However, state of the art algorithms to estimate the entropy rate have markedly slow convergence; making such entropic approaches non-viable in practice. We present here a fundamentally new approach to estimate entropy rates, which is demonstrated to converge significantly faster in terms of input data lengths, and is shown to be effective in diverse applications ranging from the estimation of the entropy rate of English texts to the estimation of complexity of chaotic dynamical systems. Additionally, the convergence rate of entropy estimates do not follow from any standard limit theorem, and reported algorithms fail to provide any confidence bounds on the computed values. Exploiting a connection to the theory of probabilistic automata, we establish a convergence rate of $O(\log \vert s \vert/\sqrt[3]{\vert s \vert})$ as a function of the input length $\vert s \vert$, which then yields explicit uncertainty estimates, as well as required data lengths to satisfy pre-specified confidence bounds.
Data Smashing
Jan 03, 2014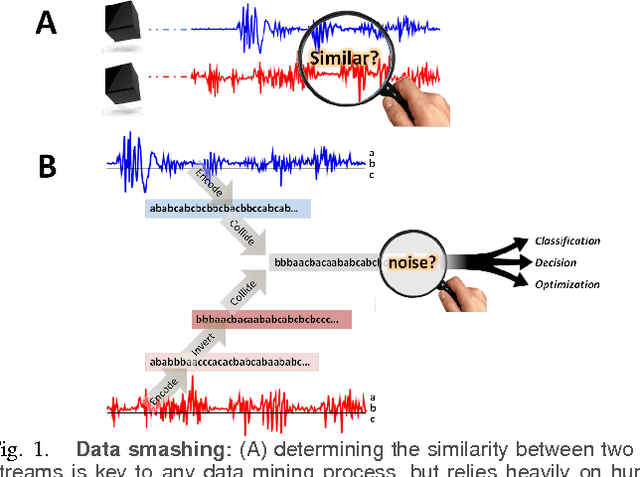
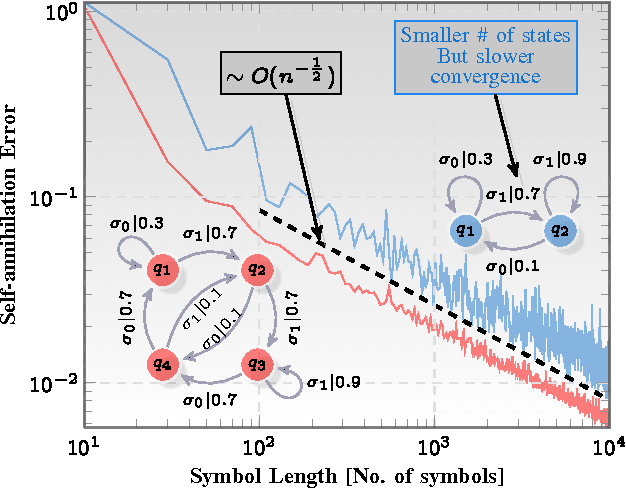
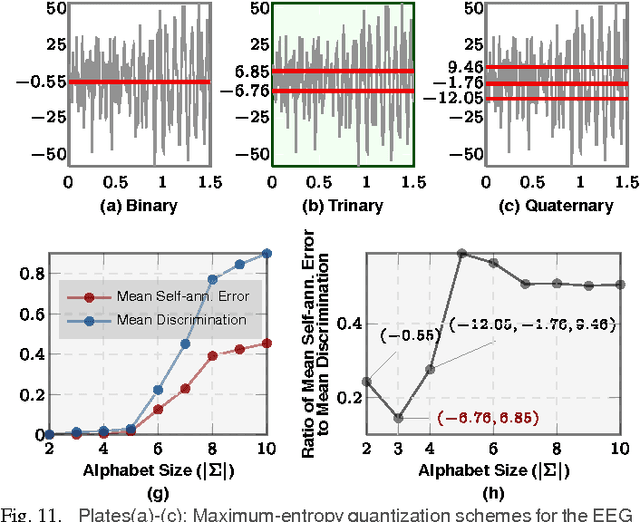
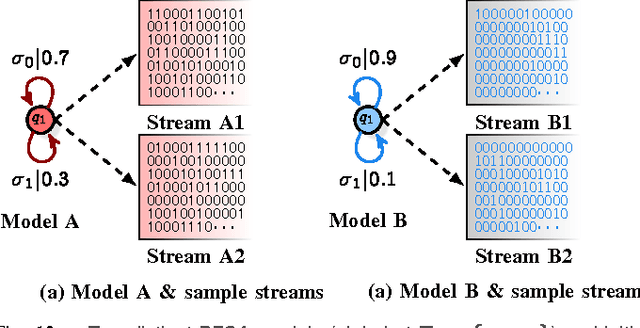
Abstract:Investigation of the underlying physics or biology from empirical data requires a quantifiable notion of similarity - when do two observed data sets indicate nearly identical generating processes, and when they do not. The discriminating characteristics to look for in data is often determined by heuristics designed by experts, $e.g.$, distinct shapes of "folded" lightcurves may be used as "features" to classify variable stars, while determination of pathological brain states might require a Fourier analysis of brainwave activity. Finding good features is non-trivial. Here, we propose a universal solution to this problem: we delineate a principle for quantifying similarity between sources of arbitrary data streams, without a priori knowledge, features or training. We uncover an algebraic structure on a space of symbolic models for quantized data, and show that such stochastic generators may be added and uniquely inverted; and that a model and its inverse always sum to the generator of flat white noise. Therefore, every data stream has an anti-stream: data generated by the inverse model. Similarity between two streams, then, is the degree to which one, when summed to the other's anti-stream, mutually annihilates all statistical structure to noise. We call this data smashing. We present diverse applications, including disambiguation of brainwaves pertaining to epileptic seizures, detection of anomalous cardiac rhythms, and classification of astronomical objects from raw photometry. In our examples, the data smashing principle, without access to any domain knowledge, meets or exceeds the performance of specialized algorithms tuned by domain experts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge