Principal-Agent Reinforcement Learning

Contracts are the economic framework which allows a principal to delegate a task to an agent -- despite misaligned interests, and even without directly observing the agent's actions. In many modern reinforcement learning settings, self-interested agents learn to perform a multi-stage task delegated to them by a principal. We explore the significant potential of utilizing contracts to incentivize the agents. We model the delegated task as an MDP, and study a stochastic game between the principal and agent where the principal learns what contracts to use, and the agent learns an MDP policy in response. We present a learning-based algorithm for optimizing the principal's contracts, which provably converges to the subgame-perfect equilibrium of the principal-agent game. A deep RL implementation allows us to apply our method to very large MDPs with unknown transition dynamics. We extend our approach to multiple agents, and demonstrate its relevance to resolving a canonical sequential social dilemma with minimal intervention to agent rewards.

Incentivizing Quality Text Generation via Statistical Contracts

While the success of large language models (LLMs) increases demand for machine-generated text, current pay-per-token pricing schemes create a misalignment of incentives known in economics as moral hazard: Text-generating agents have strong incentive to cut costs by preferring a cheaper model over the cutting-edge one, and this can be done "behind the scenes" since the agent performs inference internally. In this work, we approach this issue from an economic perspective, by proposing a pay-for-performance, contract-based framework for incentivizing quality. We study a principal-agent game where the agent generates text using costly inference, and the contract determines the principal's payment for the text according to an automated quality evaluation. Since standard contract theory is inapplicable when internal inference costs are unknown, we introduce cost-robust contracts. As our main theoretical contribution, we characterize optimal cost-robust contracts through a direct correspondence to optimal composite hypothesis tests from statistics, generalizing a result of Saig et al. (NeurIPS'23). We evaluate our framework empirically by deriving contracts for a range of objectives and LLM evaluation benchmarks, and find that cost-robust contracts sacrifice only a marginal increase in objective value compared to their cost-aware counterparts.

Strategy-Proof Auctions through Conformal Prediction

Auctions are key for maximizing sellers' revenue and ensuring truthful bidding among buyers. Recently, an approach known as differentiable economics based on deep learning shows promise in learning optimal auction mechanisms for multiple items and participants. However, this approach has no guarantee of strategy-proofness at test time. Strategy-proofness is crucial as it ensures that buyers are incentivized to bid their true valuations, leading to optimal and fair auction outcomes without the risk of manipulation. Building on conformal prediction, we introduce a novel approach to achieve strategy-proofness with rigorous statistical guarantees. The key novelties of our method are: (i) the formulation of a regret prediction model, used to quantify at test time violations of strategy-proofness; and (ii) an auction acceptance rule that leverages the predicted regret to ensure that for a new auction, the data-driven mechanism meets the strategy-proofness requirement with high probability (e.g., 99\%). Numerical experiments demonstrate the necessity for rigorous guarantees, the validity of our theoretical results, and the applicability of our proposed method.

MAC Advice for Facility Location Mechanism Design

Algorithms with predictions have attracted much attention in the last years across various domains, including variants of facility location, as a way to surpass traditional worst-case analyses. We study the $k$-facility location mechanism design problem, where the $n$ agents are strategic and might misreport their location. Unlike previous models, where predictions are for the $k$ optimal facility locations, we receive $n$ predictions for the locations of each of the agents. However, these predictions are only "mostly" and "approximately" correct (or MAC for short) -- i.e., some $\delta$-fraction of the predicted locations are allowed to be arbitrarily incorrect, and the remainder of the predictions are allowed to be correct up to an $\varepsilon$-error. We make no assumption on the independence of the errors. Can such predictions allow us to beat the current best bounds for strategyproof facility location? We show that the $1$-median (geometric median) of a set of points is naturally robust under corruptions, which leads to an algorithm for single-facility location with MAC predictions. We extend the robustness result to a "balanced" variant of the $k$ facilities case. Without balancedness, we show that robustness completely breaks down, even for the setting of $k=2$ facilities on a line. For this "unbalanced" setting, we devise a truthful random mechanism that outperforms the best known result of Lu et al. [2010], which does not use predictions. En route, we introduce the problem of "second" facility location (when the first facility's location is already fixed). Our findings on the robustness of the $1$-median and more generally $k$-medians may be of independent interest, as quantitative versions of classic breakdown-point results in robust statistics.

Contracting with a Learning Agent

Many real-life contractual relations differ completely from the clean, static model at the heart of principal-agent theory. Typically, they involve repeated strategic interactions of the principal and agent, taking place under uncertainty and over time. While appealing in theory, players seldom use complex dynamic strategies in practice, often preferring to circumvent complexity and approach uncertainty through learning. We initiate the study of repeated contracts with a learning agent, focusing on agents who achieve no-regret outcomes. Optimizing against a no-regret agent is a known open problem in general games; we achieve an optimal solution to this problem for a canonical contract setting, in which the agent's choice among multiple actions leads to success/failure. The solution has a surprisingly simple structure: for some $\alpha > 0$, initially offer the agent a linear contract with scalar $\alpha$, then switch to offering a linear contract with scalar $0$. This switch causes the agent to ``free-fall'' through their action space and during this time provides the principal with non-zero reward at zero cost. Despite apparent exploitation of the agent, this dynamic contract can leave \emph{both} players better off compared to the best static contract. Our results generalize beyond success/failure, to arbitrary non-linear contracts which the principal rescales dynamically. Finally, we quantify the dependence of our results on knowledge of the time horizon, and are the first to address this consideration in the study of strategizing against learning agents.

Deep Contract Design via Discontinuous Piecewise Affine Neural Networks

Contract design involves a principal who establishes contractual agreements about payments for outcomes that arise from the actions of an agent. In this paper, we initiate the study of deep learning for the automated design of optimal contracts. We formulate this as an offline learning problem, where a deep network is used to represent the principal's expected utility as a function of the design of a contract. We introduce a novel representation: the Discontinuous ReLU (DeLU) network, which models the principal's utility as a discontinuous piecewise affine function where each piece corresponds to the agent taking a particular action. DeLU networks implicitly learn closed-form expressions for the incentive compatibility constraints of the agent and the utility maximization objective of the principal, and support parallel inference on each piece through linear programming or interior-point methods that solve for optimal contracts. We provide empirical results that demonstrate success in approximating the principal's utility function with a small number of training samples and scaling to find approximately optimal contracts on problems with a large number of actions and outcomes.

Delegated Classification

When machine learning is outsourced to a rational agent, conflicts of interest might arise and severely impact predictive performance. In this work, we propose a theoretical framework for incentive-aware delegation of machine learning tasks. We model delegation as a principal-agent game, in which accurate learning can be incentivized by the principal using performance-based contracts. Adapting the economic theory of contract design to this setting, we define budget-optimal contracts and prove they take a simple threshold form under reasonable assumptions. In the binary-action case, the optimality of such contracts is shown to be equivalent to the classic Neyman-Pearson lemma, establishing a formal connection between contract design and statistical hypothesis testing. Empirically, we demonstrate that budget-optimal contracts can be constructed using small-scale data, leveraging recent advances in the study of learning curves and scaling laws. Performance and economic outcomes are evaluated using synthetic and real-world classification tasks.

Strategic Representation

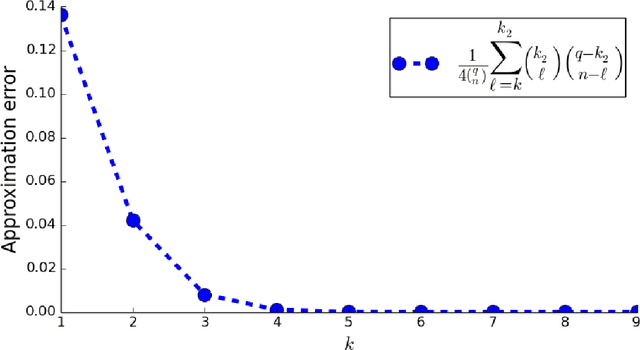
Humans have come to rely on machines for reducing excessive information to manageable representations. But this reliance can be abused -- strategic machines might craft representations that manipulate their users. How can a user make good choices based on strategic representations? We formalize this as a learning problem, and pursue algorithms for decision-making that are robust to manipulation. In our main setting of interest, the system represents attributes of an item to the user, who then decides whether or not to consume. We model this interaction through the lens of strategic classification (Hardt et al. 2016), reversed: the user, who learns, plays first; and the system, which responds, plays second. The system must respond with representations that reveal `nothing but the truth' but need not reveal the entire truth. Thus, the user faces the problem of learning set functions under strategic subset selection, which presents distinct algorithmic and statistical challenges. Our main result is a learning algorithm that minimizes error despite strategic representations, and our theoretical analysis sheds light on the trade-off between learning effort and susceptibility to manipulation.

Strategic Classification in the Dark

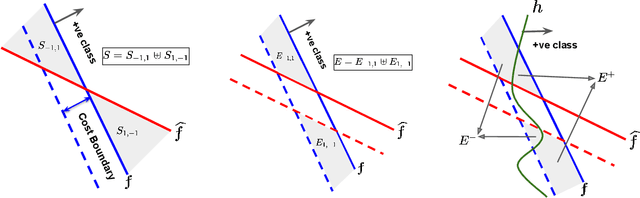
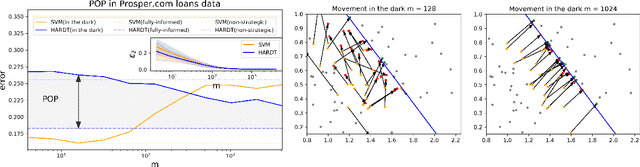
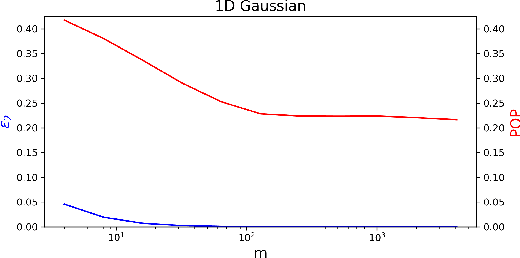
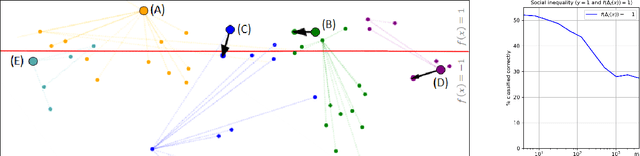
Strategic classification studies the interaction between a classification rule and the strategic agents it governs. Under the assumption that the classifier is known, rational agents respond to it by manipulating their features. However, in many real-life scenarios of high-stake classification (e.g., credit scoring), the classifier is not revealed to the agents, which leads agents to attempt to learn the classifier and game it too. In this paper we generalize the strategic classification model to such scenarios. We define the price of opacity as the difference in prediction error between opaque and transparent strategy-robust classifiers, characterize it, and give a sufficient condition for this price to be strictly positive, in which case transparency is the recommended policy. Our experiments show how Hardt et al.'s robust classifier is affected by keeping agents in the dark.