Differentiable Causal Discovery Under Unmeasured Confounding

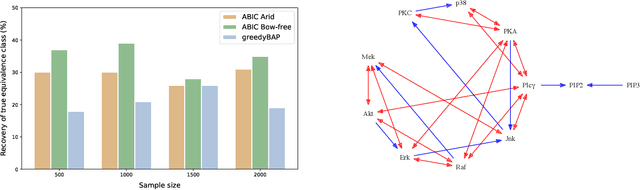
The data drawn from biological, economic, and social systems are often confounded due to the presence of unmeasured variables. Prior work in causal discovery has focused on discrete search procedures for selecting acyclic directed mixed graphs (ADMGs), specifically ancestral ADMGs, that encode ordinary conditional independence constraints among the observed variables of the system. However, confounded systems also exhibit more general equality restrictions that cannot be represented via these graphs, placing a limit on the kinds of structures that can be learned using ancestral ADMGs. In this work, we derive differentiable algebraic constraints that fully characterize the space of ancestral ADMGs, as well as more general classes of ADMGs, arid ADMGs and bow-free ADMGs, that capture all equality restrictions on the observed variables. We use these constraints to cast causal discovery as a continuous optimization problem and design differentiable procedures to find the best fitting ADMG when the data comes from a confounded linear system of equations with correlated errors. We demonstrate the efficacy of our method through simulations and application to a protein expression dataset.

Path Dependent Structural Equation Models

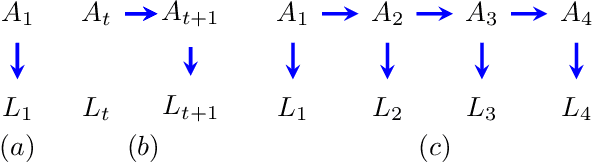
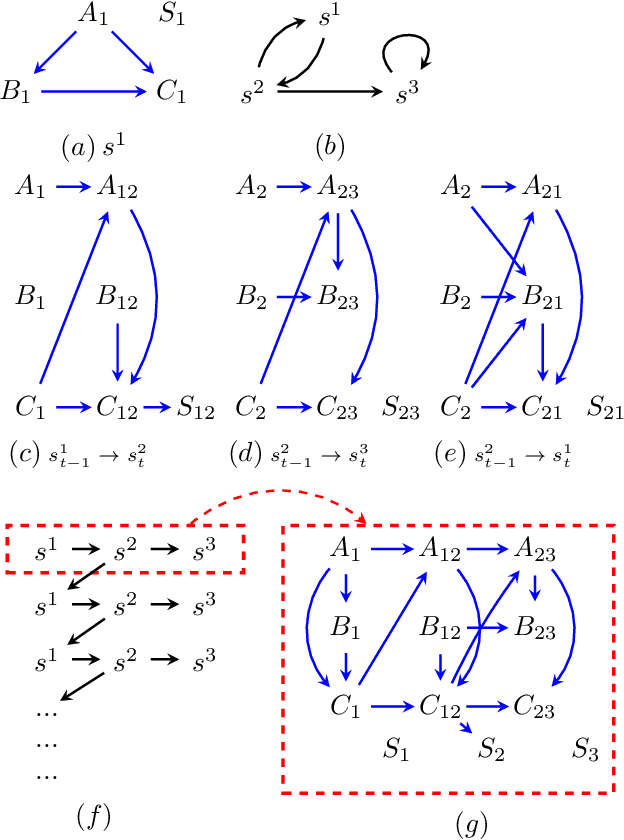
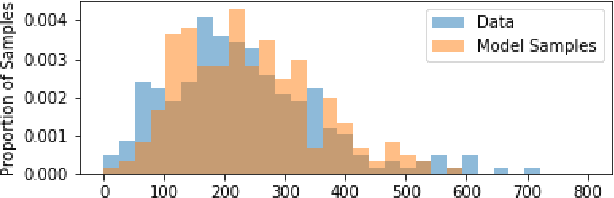
Causal analyses of longitudinal data generally assume structure that is invariant over time. Graphical causal models describe these data using a single causal diagram repeated at every time step. In structured systems that transition between qualitatively different states in discrete time steps, such an approach is deficient on two fronts. First, time-varying variables may have state-specific causal relationships that need to be captured. Second, an intervention can result in state transitions downstream of the intervention different from thoseactually observed in the data. In other words, interventions may counterfactually alter the subsequent temporal evolution of the system. We introduce a generalization of causal graphical models, Path Dependent Structural Equation Models (PDSEMs), that can describe such systems. We show how causal inference may be performed in such models and illustrate its use in simulations and data obtained from a septoplasty surgical procedure.

Deriving Bounds and Inequality Constraints Using LogicalRelations Among Counterfactuals

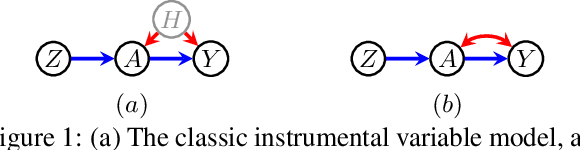
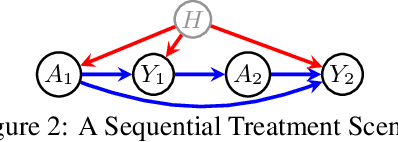
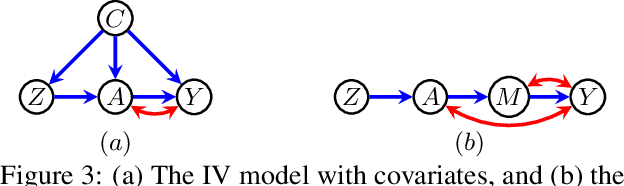
Causal parameters may not be point identified in the presence of unobserved confounding. However, information about non-identified parameters, in the form of bounds, may still be recovered from the observed data in some cases. We develop a new general method for obtaining bounds on causal parameters using rules of probability and restrictions on counterfactuals implied by causal graphical models. We additionally provide inequality constraints on functionals of the observed data law implied by such causal models. Our approach is motivated by the observation that logical relations between identified and non-identified counterfactual events often yield information about non-identified events. We show that this approach is powerful enough to recover known sharp bounds and tight inequality constraints, and to derive novel bounds and constraints.

A Semiparametric Approach to Interpretable Machine Learning

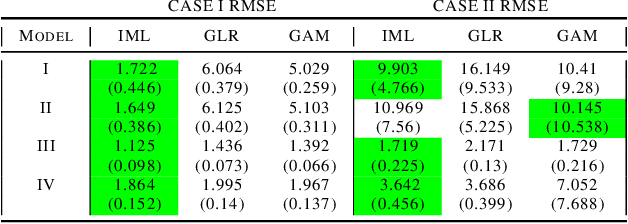
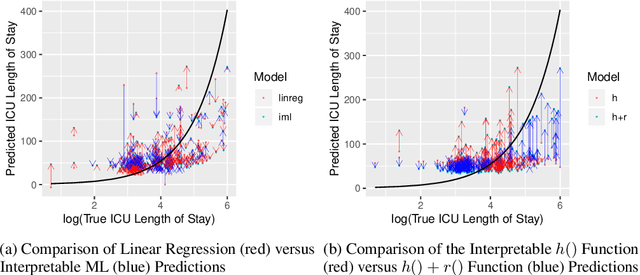
Black box models in machine learning have demonstrated excellent predictive performance in complex problems and high-dimensional settings. However, their lack of transparency and interpretability restrict the applicability of such models in critical decision-making processes. In order to combat this shortcoming, we propose a novel approach to trading off interpretability and performance in prediction models using ideas from semiparametric statistics, allowing us to combine the interpretability of parametric regression models with performance of nonparametric methods. We achieve this by utilizing a two-piece model: the first piece is interpretable and parametric, to which a second, uninterpretable residual piece is added. The performance of the overall model is optimized using methods from the sufficient dimension reduction literature. Influence function based estimators are derived and shown to be doubly robust. This allows for use of approaches such as double Machine Learning in estimating our model parameters. We illustrate the utility of our approach via simulation studies and a data application based on predicting the length of stay in the intensive care unit among surgery patients.

Explaining The Behavior Of Black-Box Prediction Algorithms With Causal Learning

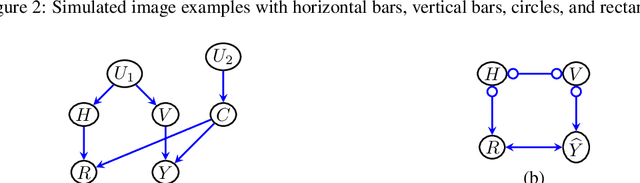
We propose to explain the behavior of black-box prediction methods (e.g., deep neural networks trained on image pixel data) using causal graphical models. Specifically, we explore learning the structure of a causal graph where the nodes represent prediction outcomes along with a set of macro-level "interpretable" features, while allowing for arbitrary unmeasured confounding among these variables. The resulting graph may indicate which of the interpretable features, if any, are possible causes of the prediction outcome and which may be merely associated with prediction outcomes due to confounding. The approach is motivated by a counterfactual theory of causal explanation wherein good explanations point to factors which are "difference-makers" in an interventionist sense. The resulting analysis may be useful in algorithm auditing and evaluation, by identifying features which make a causal difference to the algorithm's output.

Identification Methods With Arbitrary Interventional Distributions as Inputs

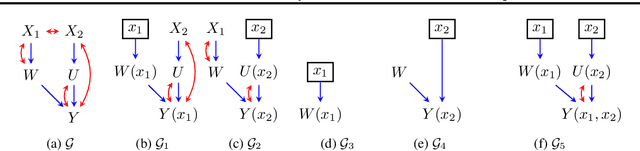
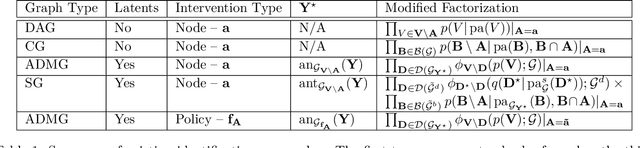
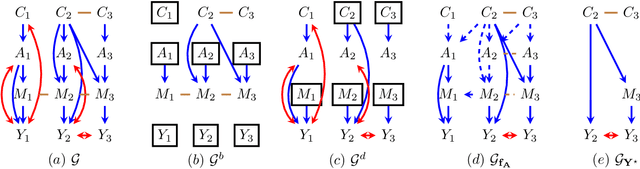
Causal inference quantifies cause-effect relationships by estimating counterfactual parameters from data. This entails using \emph{identification theory} to establish a link between counterfactual parameters of interest and distributions from which data is available. A line of work characterized non-parametric identification for a wide variety of causal parameters in terms of the \emph{observed data distribution}. More recently, identification results have been extended to settings where experimental data from interventional distributions is also available. In this paper, we use Single World Intervention Graphs and a nested factorization of models associated with mixed graphs to give a very simple view of existing identification theory for experimental data. We use this view to yield general identification algorithms for settings where the input distributions consist of an arbitrary set of observational and experimental distributions, including marginal and conditional distributions. We show that for problems where inputs are interventional marginal distributions of a certain type (ancestral marginals), our algorithm is complete.

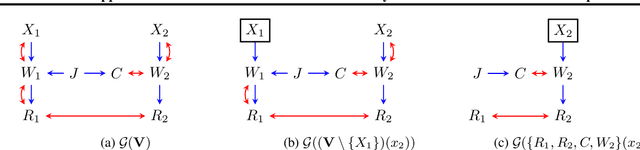
Full Law Identification In Graphical Models Of Missing Data: Completeness Results

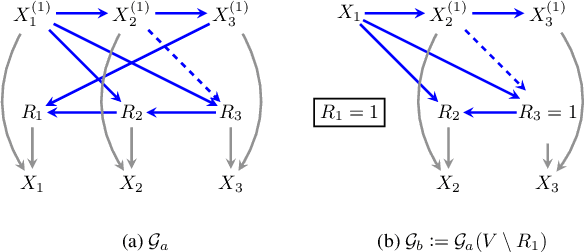
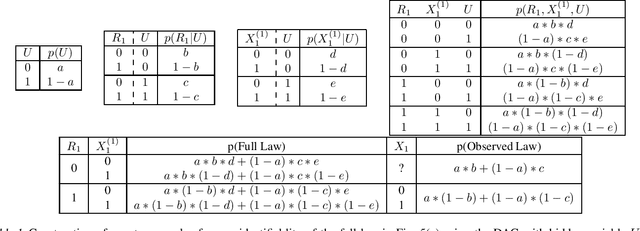
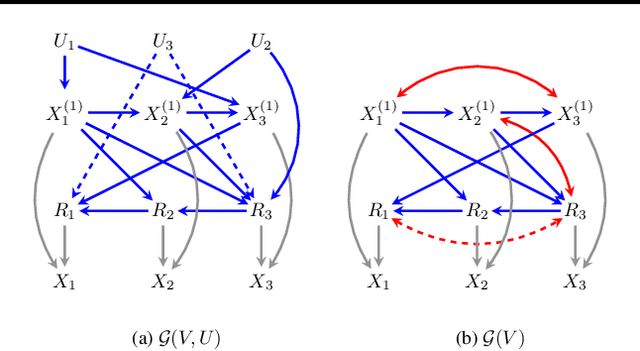
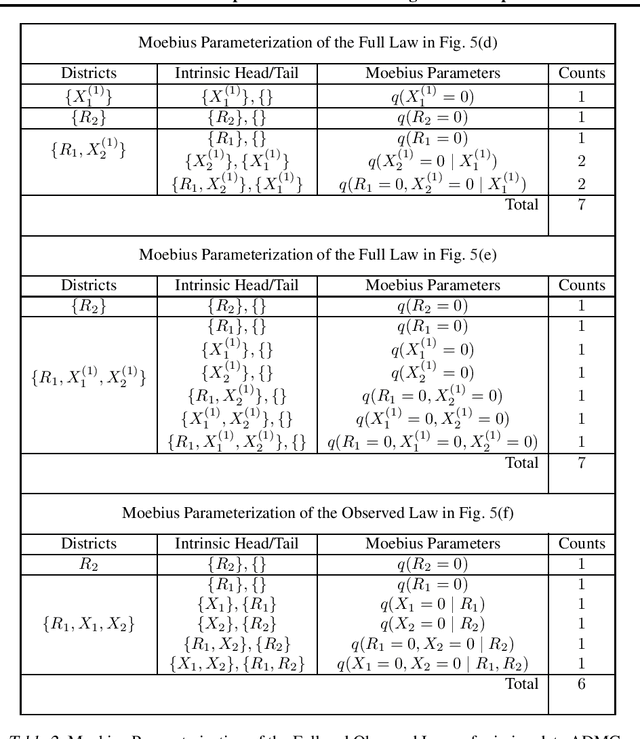
Missing data has the potential to affect analyses conducted in all fields of scientific study, including healthcare, economics, and the social sciences. Several approaches to unbiased inference in the presence of non-ignorable missingness rely on the specification of the target distribution and its missingness process as a probability distribution that factorizes with respect to a directed acyclic graph. In this paper, we address the longstanding question of the characterization of models that are identifiable within this class of missing data distributions. We provide the first completeness result in this field of study -- necessary and sufficient graphical conditions under which, the full data distribution can be recovered from the observed data distribution. We then simultaneously address issues that may arise due to the presence of both missing data and unmeasured confounding, by extending these graphical conditions and proofs of completeness, to settings where some variables are not just missing, but completely unobserved.

General Identification of Dynamic Treatment Regimes Under Interference

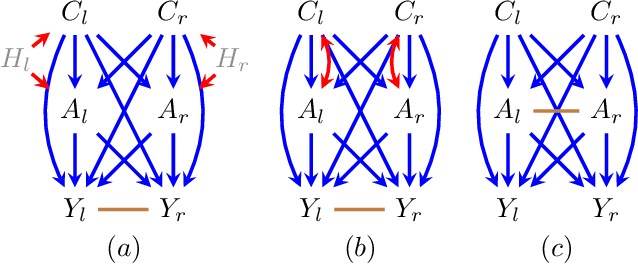
In many applied fields, researchers are often interested in tailoring treatments to unit-level characteristics in order to optimize an outcome of interest. Methods for identifying and estimating treatment policies are the subject of the dynamic treatment regime literature. Separately, in many settings the assumption that data are independent and identically distributed does not hold due to inter-subject dependence. The phenomenon where a subject's outcome is dependent on his neighbor's exposure is known as interference. These areas intersect in myriad real-world settings. In this paper we consider the problem of identifying optimal treatment policies in the presence of interference. Using a general representation of interference, via Lauritzen-Wermuth-Freydenburg chain graphs (Lauritzen and Richardson, 2002), we formalize a variety of policy interventions under interference and extend existing identification theory (Tian, 2008; Sherman and Shpitser, 2018). Finally, we illustrate the efficacy of policy maximization under interference in a simulation study.

Semiparametric Inference For Causal Effects In Graphical Models With Hidden Variables

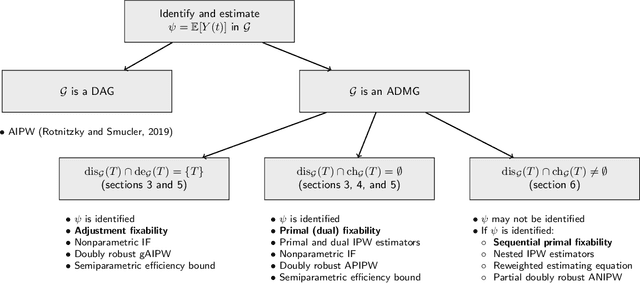
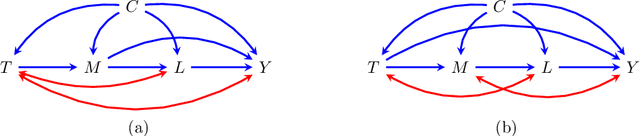
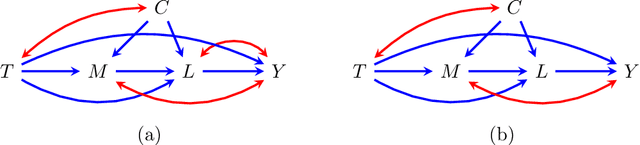
The last decade witnessed the development of algorithms that completely solve the identifiability problem for causal effects in hidden variable causal models associated with directed acyclic graphs. However, much of this machinery remains underutilized in practice owing to the complexity of estimating identifying functionals yielded by these algorithms. In this paper, we provide simple graphical criteria and semiparametric estimators that bridge the gap between identification and estimation for causal effects involving a single treatment and a single outcome. First, we provide influence function based doubly robust estimators that cover a significant subset of hidden variable causal models where the effect is identifiable. We further characterize an important subset of this class for which we demonstrate how to derive the estimator with the lowest asymptotic variance, i.e., one that achieves the semiparametric efficiency bound. Finally, we provide semiparametric estimators for any single treatment causal effect parameter identified via the aforementioned algorithms. The resulting estimators resemble influence function based estimators that are sequentially reweighted, and exhibit a partial double robustness property, provided the parts of the likelihood corresponding to a set of weight models are correctly specified. Our methods are easy to implement and we demonstrate their utility through simulations.

Counterexamples to "The Blessings of Multiple Causes" by Wang and Blei

This brief note is meant to complement our previous comment on "The Blessings of Multiple Causes" by Wang and Blei (2019). We provide a more succinct and transparent explanation of the fact that the deconfounder does not control for multi-cause confounding. The argument given in Wang and Blei (2019) makes two mistakes: (1) attempting to infer independence conditional on one variable from independence conditional on a different, unrelated variable, and (2) attempting to infer joint independence from pairwise independence. We give two simple counterexamples to the deconfounder claim.