Pointwise confidence estimation in the non-linear $\ell^2$-regularized least squares

We consider a high-probability non-asymptotic confidence estimation in the $\ell^2$-regularized non-linear least-squares setting with fixed design. In particular, we study confidence estimation for local minimizers of the regularized training loss. We show a pointwise confidence bound, meaning that it holds for the prediction on any given fixed test input $x$. Importantly, the proposed confidence bound scales with similarity of the test input to the training data in the implicit feature space of the predictor (for instance, becoming very large when the test input lies far outside of the training data). This desirable last feature is captured by the weighted norm involving the inverse-Hessian matrix of the objective function, which is a generalized version of its counterpart in the linear setting, $x^{\top} \text{Cov}^{-1} x$. Our generalized result can be regarded as a non-asymptotic counterpart of the classical confidence interval based on asymptotic normality of the MLE estimator. We propose an efficient method for computing the weighted norm, which only mildly exceeds the cost of a gradient computation of the loss function. Finally, we complement our analysis with empirical evidence showing that the proposed confidence bound provides better coverage/width trade-off compared to a confidence estimation by bootstrapping, which is a gold-standard method in many applications involving non-linear predictors such as neural networks.

Low-rank bias, weight decay, and model merging in neural networks

We explore the low-rank structure of the weight matrices in neural networks originating from training with Gradient Descent (GD) and Gradient Flow (GF) with $L2$ regularization (also known as weight decay). We show several properties of GD-trained deep neural networks, induced by $L2$ regularization. In particular, for a stationary point of GD we show alignment of the parameters and the gradient, norm preservation across layers, and low-rank bias: properties previously known in the context of GF solutions. Experiments show that the assumptions made in the analysis only mildly affect the observations. In addition, we investigate a multitask learning phenomenon enabled by $L2$ regularization and low-rank bias. In particular, we show that if two networks are trained, such that the inputs in the training set of one network are approximately orthogonal to the inputs in the training set of the other network, the new network obtained by simply summing the weights of the two networks will perform as well on both training sets as the respective individual networks. We demonstrate this for shallow ReLU neural networks trained by GD, as well as deep linear and deep ReLU networks trained by GF.

HONE: Higher-Order Network Embeddings

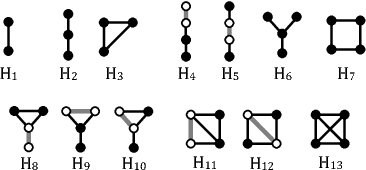
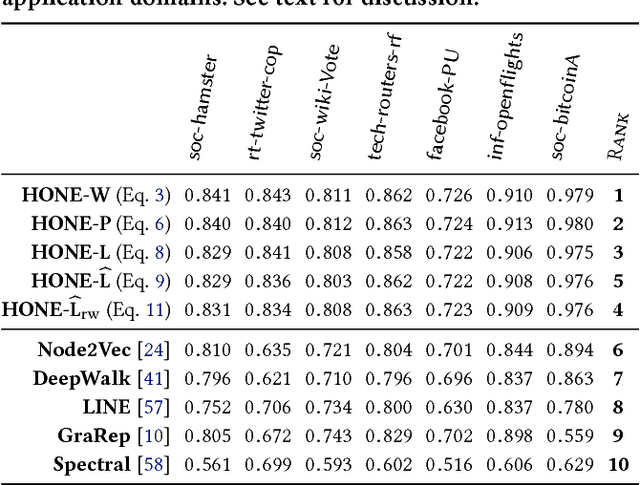
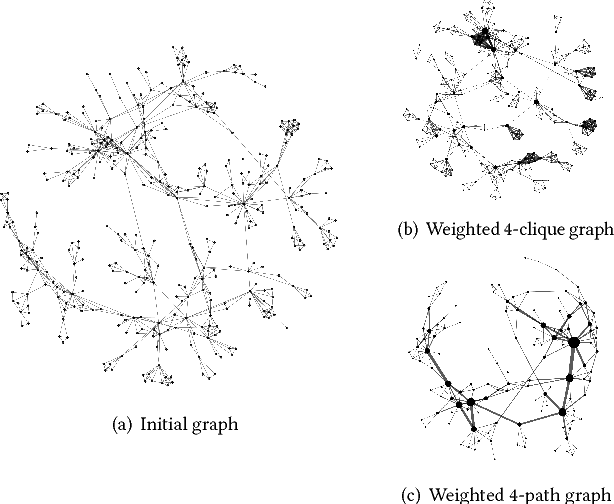
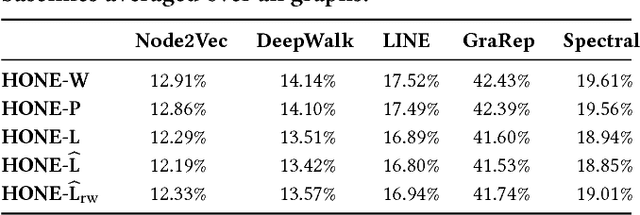
This paper describes a general framework for learning Higher-Order Network Embeddings (HONE) from graph data based on network motifs. The HONE framework is highly expressive and flexible with many interchangeable components. The experimental results demonstrate the effectiveness of learning higher-order network representations. In all cases, HONE outperforms recent embedding methods that are unable to capture higher-order structures with a mean relative gain in AUC of $19\%$ (and up to $75\%$ gain) across a wide variety of networks and embedding methods.