Misspecified Gaussian Process Bandit Optimization

We consider the problem of optimizing a black-box function based on noisy bandit feedback. Kernelized bandit algorithms have shown strong empirical and theoretical performance for this problem. They heavily rely on the assumption that the model is well-specified, however, and can fail without it. Instead, we introduce a \emph{misspecified} kernelized bandit setting where the unknown function can be $\epsilon$--uniformly approximated by a function with a bounded norm in some Reproducing Kernel Hilbert Space (RKHS). We design efficient and practical algorithms whose performance degrades minimally in the presence of model misspecification. Specifically, we present two algorithms based on Gaussian process (GP) methods: an optimistic EC-GP-UCB algorithm that requires knowing the misspecification error, and Phased GP Uncertainty Sampling, an elimination-type algorithm that can adapt to unknown model misspecification. We provide upper bounds on their cumulative regret in terms of $\epsilon$, the time horizon, and the underlying kernel, and we show that our algorithm achieves optimal dependence on $\epsilon$ with no prior knowledge of misspecification. In addition, in a stochastic contextual setting, we show that EC-GP-UCB can be effectively combined with the regret bound balancing strategy and attain similar regret bounds despite not knowing $\epsilon$.

Risk-averse Heteroscedastic Bayesian Optimization

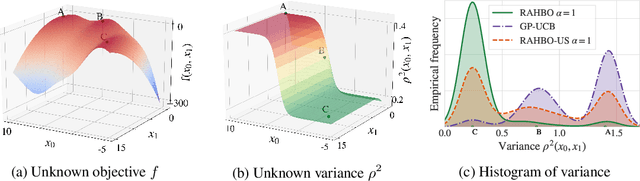
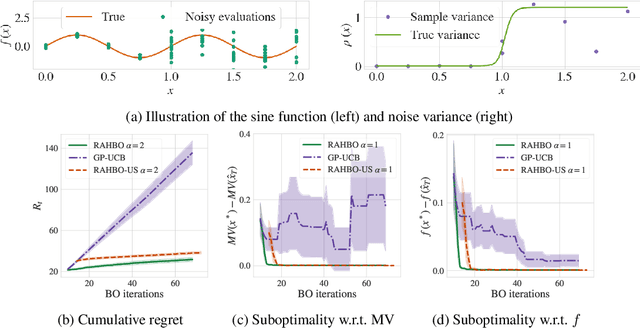
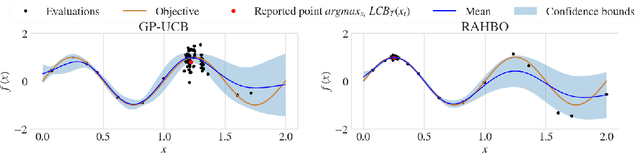
Many black-box optimization tasks arising in high-stakes applications require risk-averse decisions. The standard Bayesian optimization (BO) paradigm, however, optimizes the expected value only. We generalize BO to trade mean and input-dependent variance of the objective, both of which we assume to be unknown a priori. In particular, we propose a novel risk-averse heteroscedastic Bayesian optimization algorithm (RAHBO) that aims to identify a solution with high return and low noise variance, while learning the noise distribution on the fly. To this end, we model both expectation and variance as (unknown) RKHS functions, and propose a novel risk-aware acquisition function. We bound the regret for our approach and provide a robust rule to report the final decision point for applications where only a single solution must be identified. We demonstrate the effectiveness of RAHBO on synthetic benchmark functions and hyperparameter tuning tasks.

Contextual Games: Multi-Agent Learning with Side Information

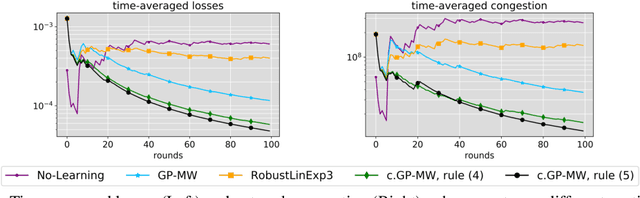
We formulate the novel class of contextual games, a type of repeated games driven by contextual information at each round. By means of kernel-based regularity assumptions, we model the correlation between different contexts and game outcomes and propose a novel online (meta) algorithm that exploits such correlations to minimize the contextual regret of individual players. We define game-theoretic notions of contextual Coarse Correlated Equilibria (c-CCE) and optimal contextual welfare for this new class of games and show that c-CCEs and optimal welfare can be approached whenever players' contextual regrets vanish. Finally, we empirically validate our results in a traffic routing experiment, where our algorithm leads to better performance and higher welfare compared to baselines that do not exploit the available contextual information or the correlations present in the game.

Efficient Model-Based Multi-Agent Mean-Field Reinforcement Learning

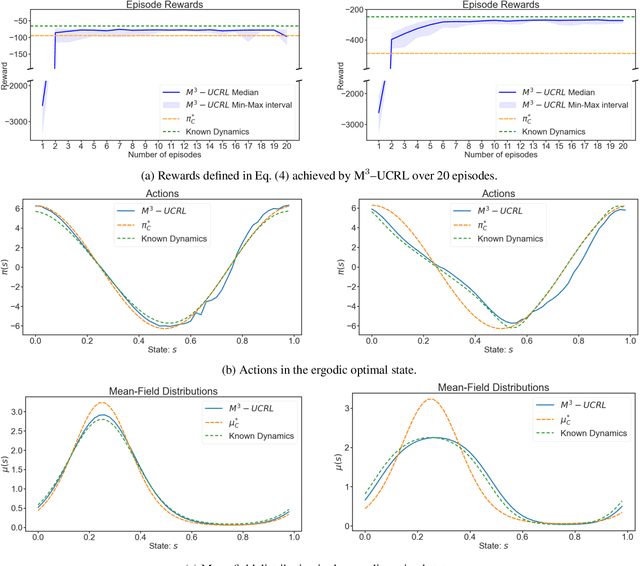
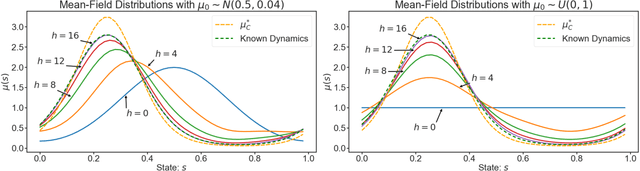
Learning in multi-agent systems is highly challenging due to the inherent complexity introduced by agents' interactions. We tackle systems with a huge population of interacting agents (e.g., swarms) via Mean-Field Control (MFC). MFC considers an asymptotically infinite population of identical agents that aim to collaboratively maximize the collective reward. Specifically, we consider the case of unknown system dynamics where the goal is to simultaneously optimize for the rewards and learn from experience. We propose an efficient model-based reinforcement learning algorithm $\text{M}^3\text{-UCRL}$ that runs in episodes and provably solves this problem. $\text{M}^3\text{-UCRL}$ uses upper-confidence bounds to balance exploration and exploitation during policy learning. Our main theoretical contributions are the first general regret bounds for model-based RL for MFC, obtained via a novel mean-field type analysis. $\text{M}^3\text{-UCRL}$ can be instantiated with different models such as neural networks or Gaussian Processes, and effectively combined with neural network policy learning. We empirically demonstrate the convergence of $\text{M}^3\text{-UCRL}$ on the swarm motion problem of controlling an infinite population of agents seeking to maximize location-dependent reward and avoid congested areas.

Combining Pessimism with Optimism for Robust and Efficient Model-Based Deep Reinforcement Learning

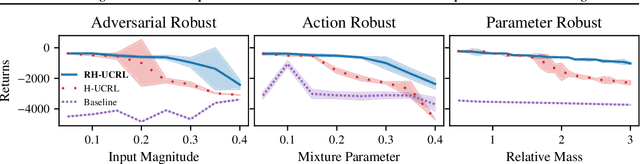
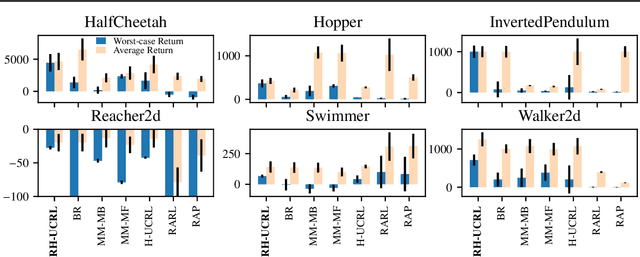
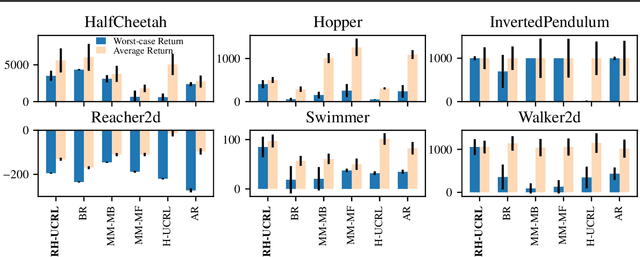
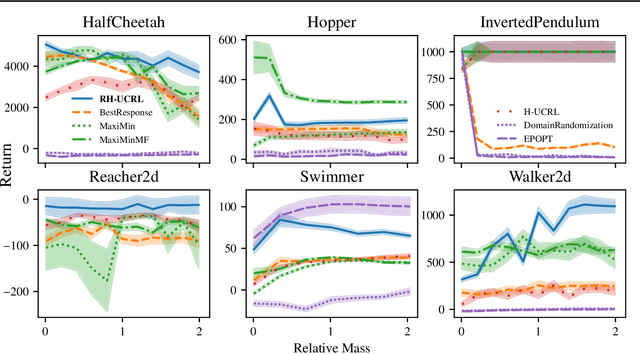
In real-world tasks, reinforcement learning (RL) agents frequently encounter situations that are not present during training time. To ensure reliable performance, the RL agents need to exhibit robustness against worst-case situations. The robust RL framework addresses this challenge via a worst-case optimization between an agent and an adversary. Previous robust RL algorithms are either sample inefficient, lack robustness guarantees, or do not scale to large problems. We propose the Robust Hallucinated Upper-Confidence RL (RH-UCRL) algorithm to provably solve this problem while attaining near-optimal sample complexity guarantees. RH-UCRL is a model-based reinforcement learning (MBRL) algorithm that effectively distinguishes between epistemic and aleatoric uncertainty and efficiently explores both the agent and adversary decision spaces during policy learning. We scale RH-UCRL to complex tasks via neural networks ensemble models as well as neural network policies. Experimentally, we demonstrate that RH-UCRL outperforms other robust deep RL algorithms in a variety of adversarial environments.

Cost-Efficient Online Hyperparameter Optimization

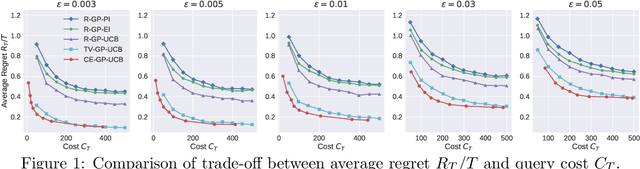
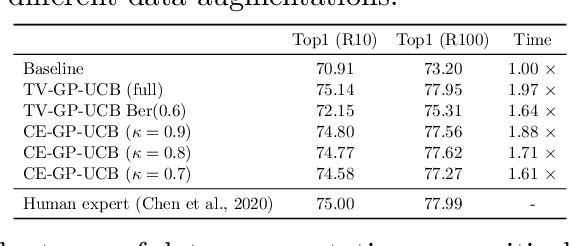
Recent work on hyperparameters optimization (HPO) has shown the possibility of training certain hyperparameters together with regular parameters. However, these online HPO algorithms still require running evaluation on a set of validation examples at each training step, steeply increasing the training cost. To decide when to query the validation loss, we model online HPO as a time-varying Bayesian optimization problem, on top of which we propose a novel \textit{costly feedback} setting to capture the concept of the query cost. Under this setting, standard algorithms are cost-inefficient as they evaluate on the validation set at every round. In contrast, the cost-efficient GP-UCB algorithm proposed in this paper queries the unknown function only when the model is less confident about current decisions. We evaluate our proposed algorithm by tuning hyperparameters online for VGG and ResNet on CIFAR-10 and ImageNet100. Our proposed online HPO algorithm reaches human expert-level performance within a single run of the experiment, while incurring only modest computational overhead compared to regular training.

Learning to Play Sequential Games versus Unknown Opponents

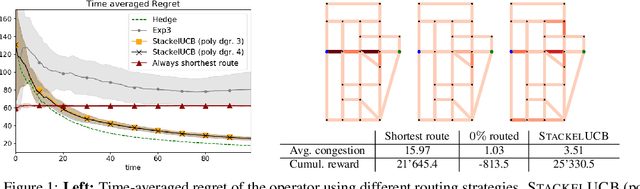
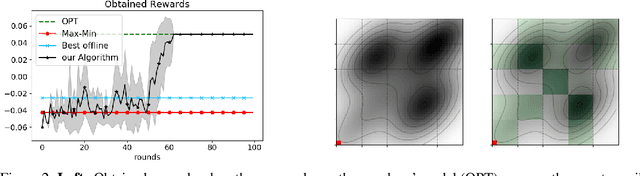
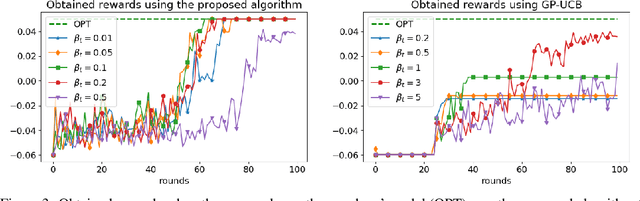
We consider a repeated sequential game between a learner, who plays first, and an opponent who responds to the chosen action. We seek to design strategies for the learner to successfully interact with the opponent. While most previous approaches consider known opponent models, we focus on the setting in which the opponent's model is unknown. To this end, we use kernel-based regularity assumptions to capture and exploit the structure in the opponent's response. We propose a novel algorithm for the learner when playing against an adversarial sequence of opponents. The algorithm combines ideas from bilevel optimization and online learning to effectively balance between exploration (learning about the opponent's model) and exploitation (selecting highly rewarding actions for the learner). Our results include algorithm's regret guarantees that depend on the regularity of the opponent's response and scale sublinearly with the number of game rounds. Moreover, we specialize our approach to repeated Stackelberg games, and empirically demonstrate its effectiveness in a traffic routing and wildlife conservation task

Stochastic Linear Bandits Robust to Adversarial Attacks

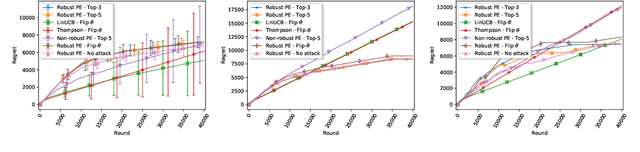
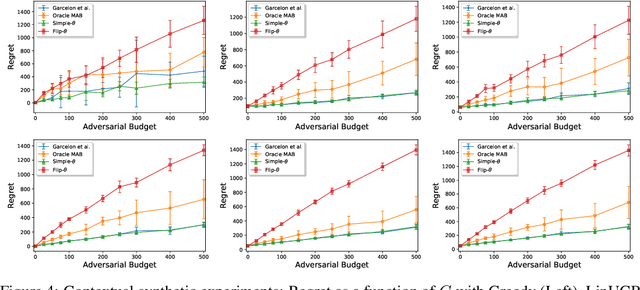
We consider a stochastic linear bandit problem in which the rewards are not only subject to random noise, but also adversarial attacks subject to a suitable budget $C$ (i.e., an upper bound on the sum of corruption magnitudes across the time horizon). We provide two variants of a Robust Phased Elimination algorithm, one that knows $C$ and one that does not. Both variants are shown to attain near-optimal regret in the non-corrupted case $C = 0$, while incurring additional additive terms respectively having a linear and quadratic dependency on $C$ in general. We present algorithm independent lower bounds showing that these additive terms are near-optimal. In addition, in a contextual setting, we revisit a setup of diverse contexts, and show that a simple greedy algorithm is provably robust with a near-optimal additive regret term, despite performing no explicit exploration and not knowing $C$.

Distributionally Robust Bayesian Optimization

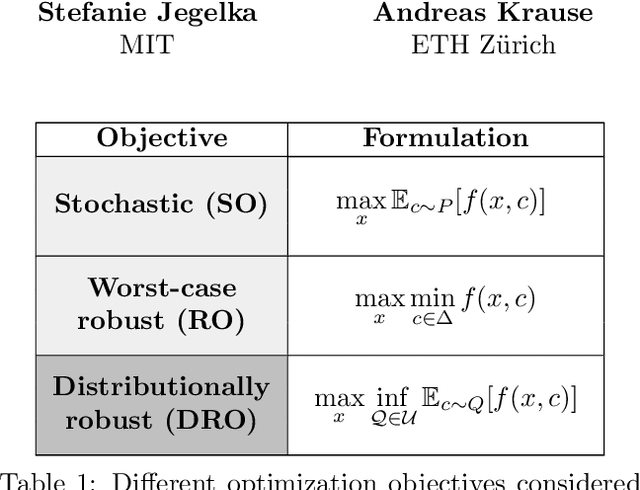
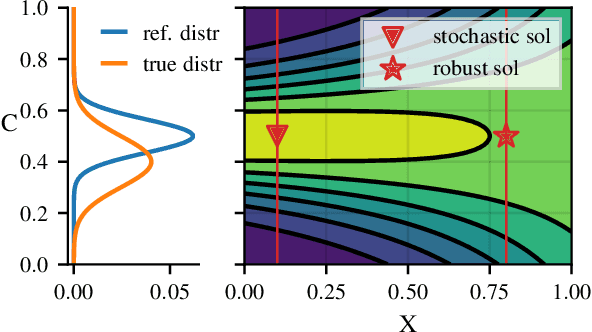
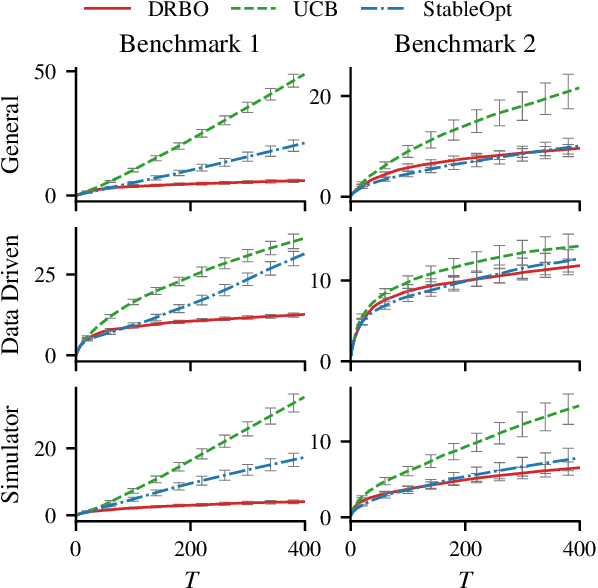
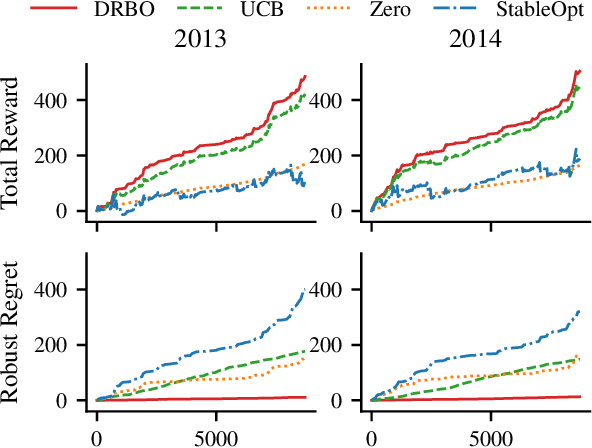
Robustness to distributional shift is one of the key challenges of contemporary machine learning. Attaining such robustness is the goal of distributionally robust optimization, which seeks a solution to an optimization problem that is worst-case robust under a specified distributional shift of an uncontrolled covariate. In this paper, we study such a problem when the distributional shift is measured via the maximum mean discrepancy (MMD). For the setting of zeroth-order, noisy optimization, we present a novel distributionally robust Bayesian optimization algorithm (DRBO). Our algorithm provably obtains sub-linear robust regret in various settings that differ in how the uncertain covariate is observed. We demonstrate the robust performance of our method on both synthetic and real-world benchmarks.

Corruption-Tolerant Gaussian Process Bandit Optimization

We consider the problem of optimizing an unknown (typically non-convex) function with a bounded norm in some Reproducing Kernel Hilbert Space (RKHS), based on noisy bandit feedback. We consider a novel variant of this problem in which the point evaluations are not only corrupted by random noise, but also adversarial corruptions. We introduce an algorithm Fast-Slow GP-UCB based on Gaussian process methods, randomized selection between two instances labeled "fast" (but non-robust) and "slow" (but robust), enlarged confidence bounds, and the principle of optimism under uncertainty. We present a novel theoretical analysis upper bounding the cumulative regret in terms of the corruption level, the time horizon, and the underlying kernel, and we argue that certain dependencies cannot be improved. We observe that distinct algorithmic ideas are required depending on whether one is required to perform well in both the corrupted and non-corrupted settings, and whether the corruption level is known or not.