Hossein Mobahi
Google Research
Data Augmentation via Structured Adversarial Perturbations
Nov 05, 2020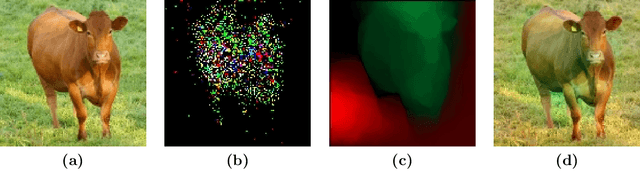
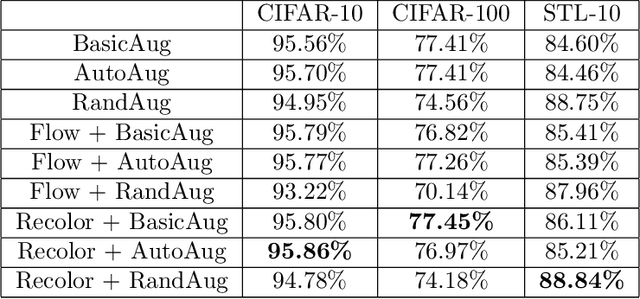

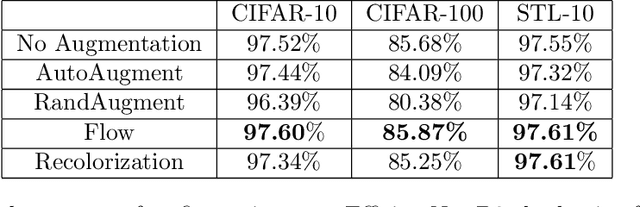
Abstract:Data augmentation is a major component of many machine learning methods with state-of-the-art performance. Common augmentation strategies work by drawing random samples from a space of transformations. Unfortunately, such sampling approaches are limited in expressivity, as they are unable to scale to rich transformations that depend on numerous parameters due to the curse of dimensionality. Adversarial examples can be considered as an alternative scheme for data augmentation. By being trained on the most difficult modifications of the inputs, the resulting models are then hopefully able to handle other, presumably easier, modifications as well. The advantage of adversarial augmentation is that it replaces sampling with the use of a single, calculated perturbation that maximally increases the loss. The downside, however, is that these raw adversarial perturbations appear rather unstructured; applying them often does not produce a natural transformation, contrary to a desirable data augmentation technique. To address this, we propose a method to generate adversarial examples that maintain some desired natural structure. We first construct a subspace that only contains perturbations with the desired structure. We then project the raw adversarial gradient onto this space to select a structured transformation that would maximally increase the loss when applied. We demonstrate this approach through two types of image transformations: photometric and geometric. Furthermore, we show that training on such structured adversarial images improves generalization.
A Unifying View on Implicit Bias in Training Linear Neural Networks
Oct 06, 2020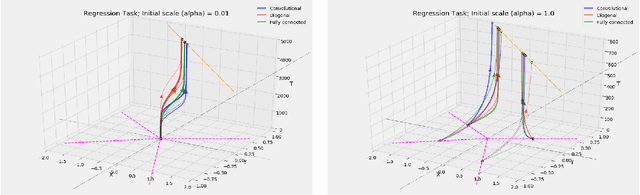
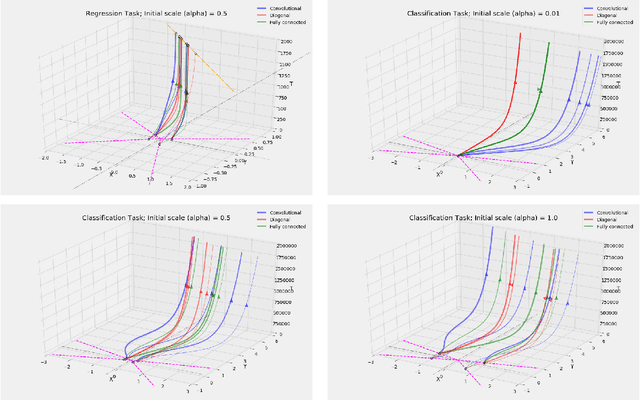
Abstract:We study the implicit bias of gradient flow (i.e., gradient descent with infinitesimal step size) on linear neural network training. We propose a tensor formulation of neural networks that includes fully-connected, diagonal, and convolutional networks as special cases, and investigate the linear version of the formulation called linear tensor networks. For $L$-layer linear tensor networks that are orthogonally decomposable, we show that gradient flow on separable classification finds a stationary point of the $\ell_{2/L}$ max-margin problem in a "transformed" input space defined by the network. For underdetermined regression, we prove that gradient flow finds a global minimum which minimizes a norm-like function that interpolates between weighted $\ell_1$ and $\ell_2$ norms in the transformed input space. Our theorems subsume existing results in the literature while removing most of the convergence assumptions. We also provide experiments that corroborate our analysis.
Sharpness-Aware Minimization for Efficiently Improving Generalization
Oct 03, 2020
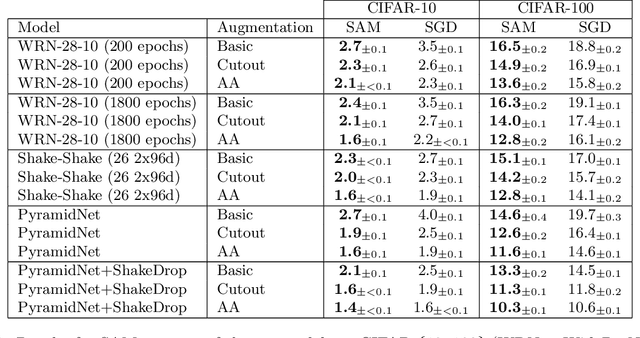
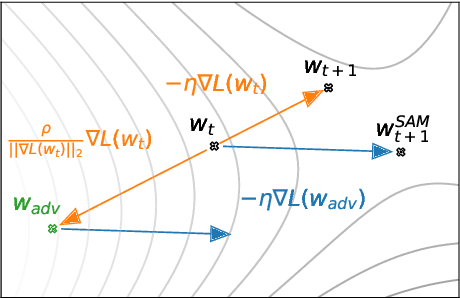
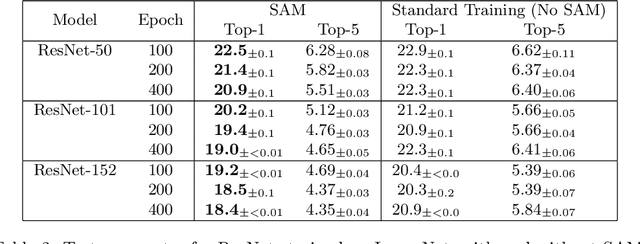
Abstract:In today's heavily overparameterized models, the value of the training loss provides few guarantees on model generalization ability. Indeed, optimizing only the training loss value, as is commonly done, can easily lead to suboptimal model quality. Motivated by the connection between geometry of the loss landscape and generalization---including a generalization bound that we prove here---we introduce a novel, effective procedure for instead simultaneously minimizing loss value and loss sharpness. In particular, our procedure, Sharpness-Aware Minimization (SAM), seeks parameters that lie in neighborhoods having uniformly low loss; this formulation results in a min-max optimization problem on which gradient descent can be performed efficiently. We present empirical results showing that SAM improves model generalization across a variety of benchmark datasets (e.g., CIFAR-{10, 100}, ImageNet, finetuning tasks) and models, yielding novel state-of-the-art performance for several. Additionally, we find that SAM natively provides robustness to label noise on par with that provided by state-of-the-art procedures that specifically target learning with noisy labels.
Self-Distillation Amplifies Regularization in Hilbert Space
Feb 25, 2020
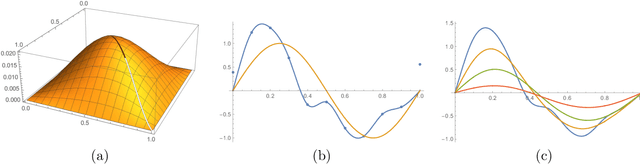
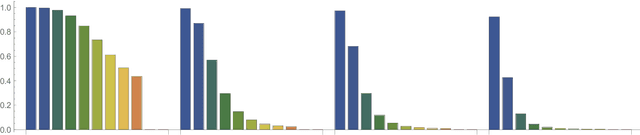
Abstract:Knowledge distillation introduced in the deep learning context is a method to transfer knowledge from one architecture to another. In particular, when the architectures are identical, this is called self-distillation. The idea is to feed in predictions of the trained model as new target values for retraining (and iterate this loop possibly a few times). It has been empirically observed that the self-distilled model often achieves higher accuracy on held out data. Why this happens, however, has been a mystery: the self-distillation dynamics does not receive any new information about the task and solely evolves by looping over training. To the best of our knowledge, there is no rigorous understanding of why this happens. This work provides the first theoretical analysis of self-distillation. We focus on fitting a nonlinear function to training data, where the model space is Hilbert space and fitting is subject to L2 regularization in this function space. We show that self-distillation iterations modify regularization by progressively limiting the number of basis functions that can be used to represent the solution. This implies (as we also verify empirically) that while a few rounds of self-distillation may reduce over-fitting, further rounds may lead to under-fitting and thus worse performance.
Fantastic Generalization Measures and Where to Find Them
Dec 04, 2019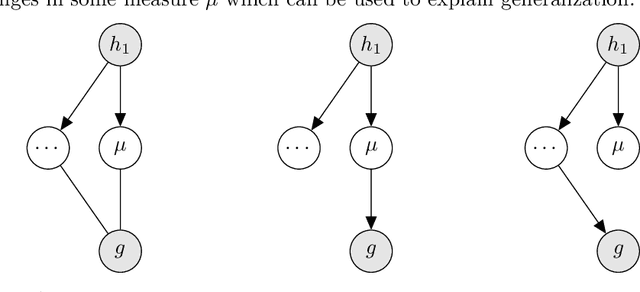
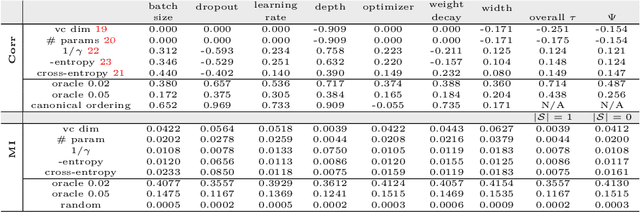
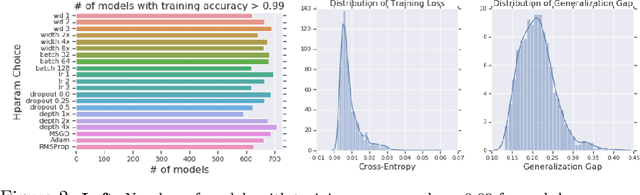
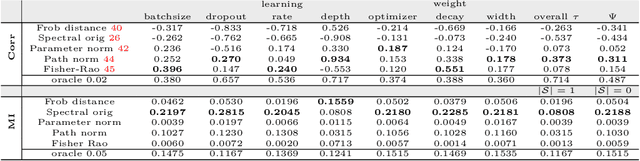
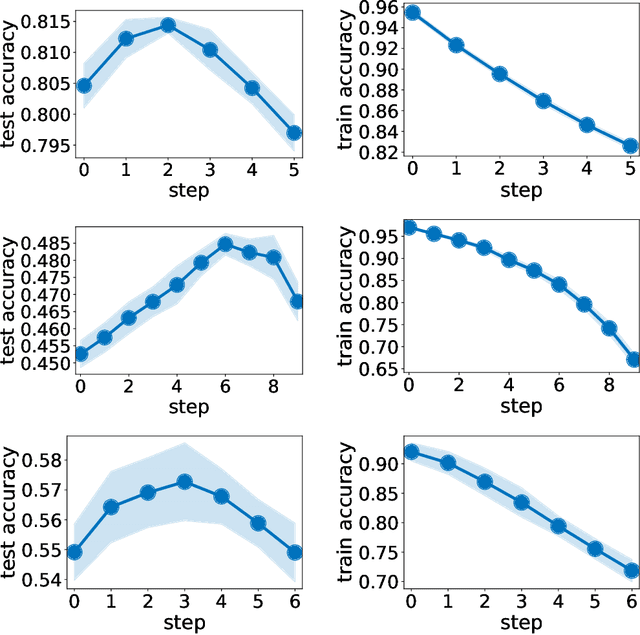
Abstract:Generalization of deep networks has been of great interest in recent years, resulting in a number of theoretically and empirically motivated complexity measures. However, most papers proposing such measures study only a small set of models, leaving open the question of whether the conclusion drawn from those experiments would remain valid in other settings. We present the first large scale study of generalization in deep networks. We investigate more then 40 complexity measures taken from both theoretical bounds and empirical studies. We train over 10,000 convolutional networks by systematically varying commonly used hyperparameters. Hoping to uncover potentially causal relationships between each measure and generalization, we analyze carefully controlled experiments and show surprising failures of some measures as well as promising measures for further research.
A Closed-Form Learned Pooling for Deep Classification Networks
Jun 10, 2019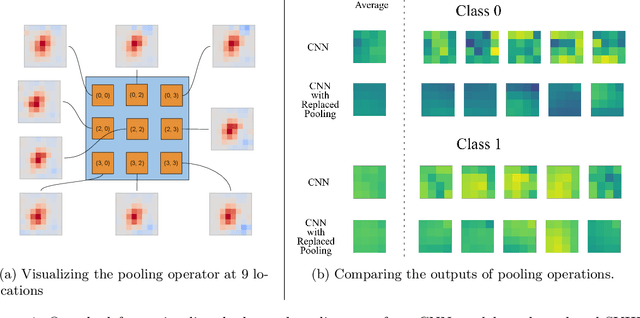
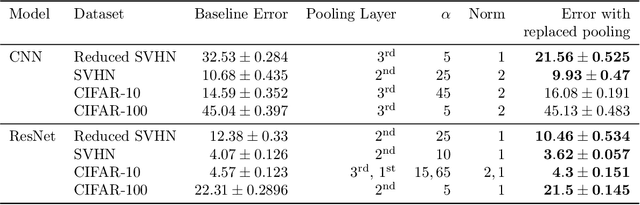
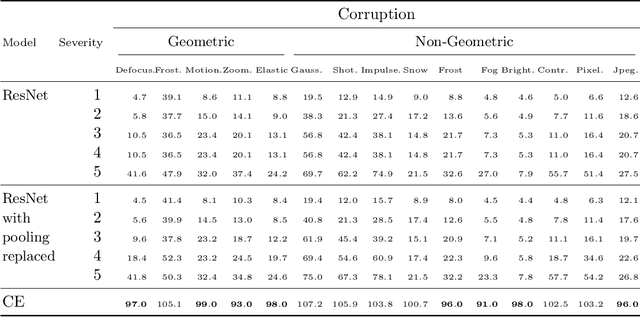
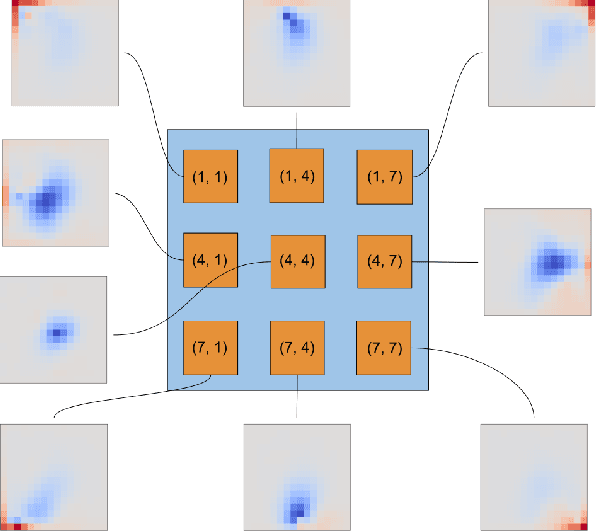
Abstract:In modern computer vision tasks, convolutional neural networks (CNNs) are indispensable for image classification tasks due to their efficiency and effectiveness. Part of their superiority compared to other architectures, comes from the fact that a single, local filter is shared across the entire image. However, there are scenarios where we may need to treat spatial locations in non-uniform manner. We see this in nature when considering how humans have evolved foveation to process different areas in their field of vision with varying levels of detail. In this paper we propose a way to enable CNNs to learn different pooling weights for each pixel location. We do so by introducing an extended definition of a pooling operator. This operator can learn a strict super-set of what can be learned by average pooling or convolutions. It has the benefit of being shared across feature maps and can be encouraged to be local or diffuse depending on the data. We show that for fixed network weights, our pooling operator can be computed in closed-form by spectral decomposition of matrices associated with class separability. Through experiments, we show that this operator benefits generalization for ResNets and CNNs on the CIFAR-10, CIFAR-100 and SVHN datasets and improves robustness to geometric corruptions and perturbations on the CIFAR-10-C and CIFAR-10-P test sets.
Semantic Redundancies in Image-Classification Datasets: The 10% You Don't Need
Jan 29, 2019
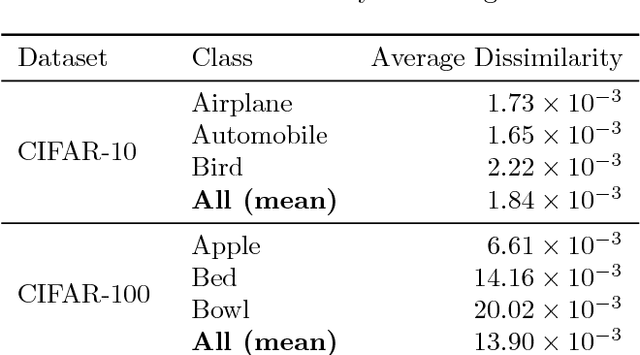
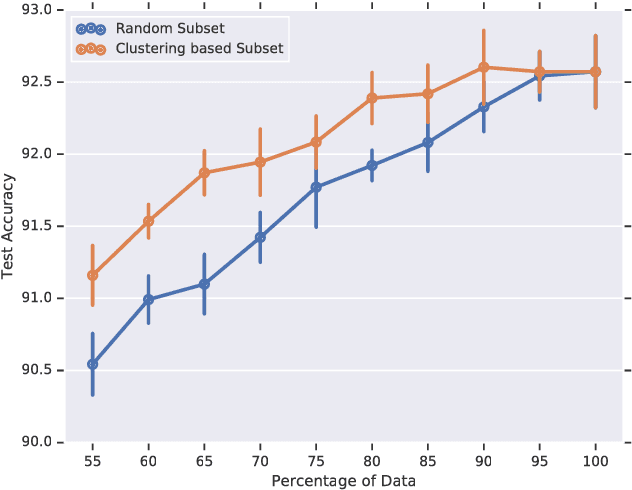

Abstract:Large datasets have been crucial to the success of deep learning models in the recent years, which keep performing better as they are trained with more labelled data. While there have been sustained efforts to make these models more data-efficient, the potential benefit of understanding the data itself, is largely untapped. Specifically, focusing on object recognition tasks, we wonder if for common benchmark datasets we can do better than random subsets of the data and find a subset that can generalize on par with the full dataset when trained on. To our knowledge, this is the first result that can find notable redundancies in CIFAR-10 and ImageNet datasets (at least 10%). Interestingly, we observe semantic correlations between required and redundant images. We hope that our findings can motivate further research into identifying additional redundancies and exploiting them for more efficient training or data-collection.
Predicting the Generalization Gap in Deep Networks with Margin Distributions
Sep 28, 2018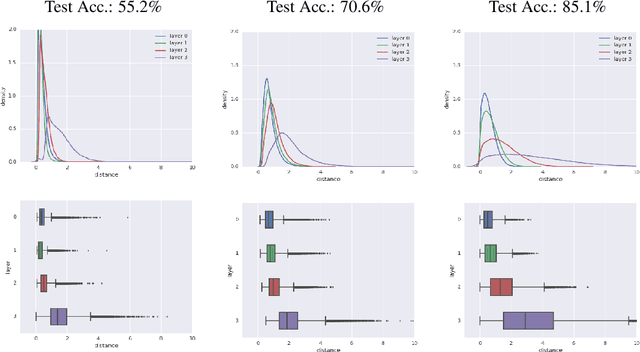
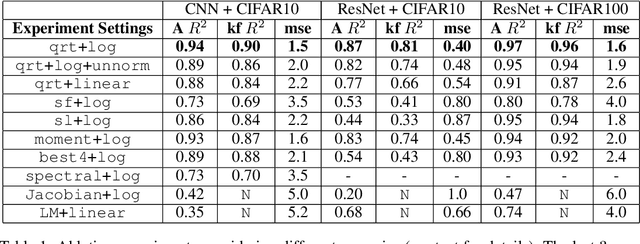
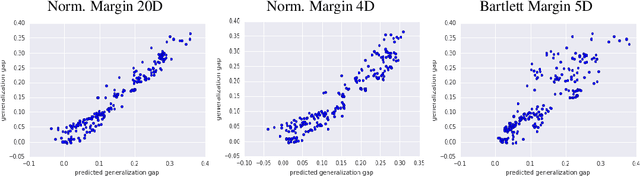
Abstract:As shown in recent research, deep neural networks can perfectly fit randomly labeled data, but with very poor accuracy on held out data. This phenomenon indicates that loss functions such as cross-entropy are not a reliable indicator of generalization. This leads to the crucial question of how generalization gap should be predicted from the training data and network parameters. In this paper, we propose such a measure, and conduct extensive empirical studies on how well it can predict the generalization gap. Our measure is based on the concept of margin distribution, which are the distances of training points to the decision boundary. We find that it is necessary to use margin distributions at multiple layers of a deep network. On the CIFAR-10 and the CIFAR-100 datasets, our proposed measure correlates very strongly with the generalization gap. In addition, we find the following other factors to be of importance: normalizing margin values for scale independence, using characterizations of margin distribution rather than just the margin (closest distance to decision boundary), and working in log space instead of linear space (effectively using a product of margins rather than a sum). Our measure can be easily applied to feedforward deep networks with any architecture and may point towards new training loss functions that could enable better generalization.
Large Margin Deep Networks for Classification
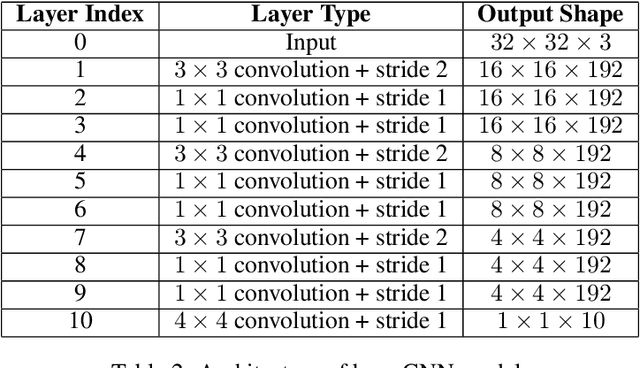
Mar 15, 2018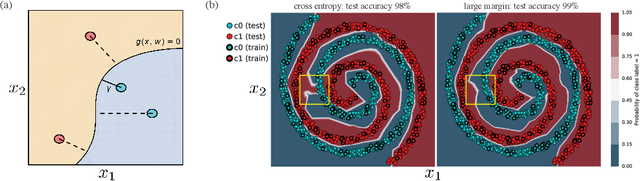
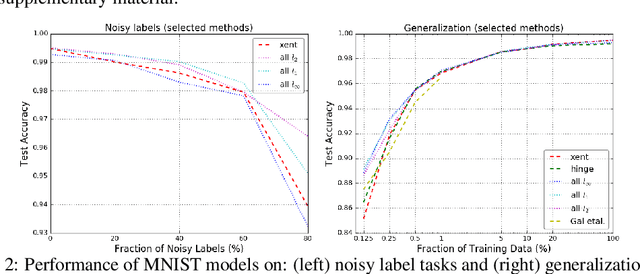
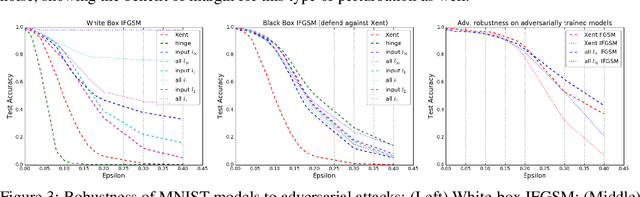
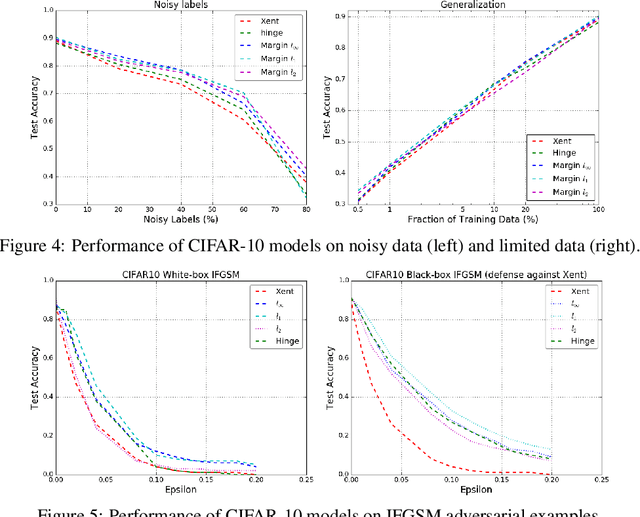
Abstract:We present a formulation of deep learning that aims at producing a large margin classifier. The notion of margin, minimum distance to a decision boundary, has served as the foundation of several theoretically profound and empirically successful results for both classification and regression tasks. However, most large margin algorithms are applicable only to shallow models with a preset feature representation; and conventional margin methods for neural networks only enforce margin at the output layer. Such methods are therefore not well suited for deep networks. In this work, we propose a novel loss function to impose a margin on any chosen set of layers of a deep network (including input and hidden layers). Our formulation allows choosing any norm on the metric measuring the margin. We demonstrate that the decision boundary obtained by our loss has nice properties compared to standard classification loss functions. Specifically, we show improved empirical results on the MNIST, CIFAR-10 and ImageNet datasets on multiple tasks: generalization from small training sets, corrupted labels, and robustness against adversarial perturbations. The resulting loss is general and complementary to existing data augmentation (such as random/adversarial input transform) and regularization techniques (such as weight decay, dropout, and batch norm).
Homotopy Analysis for Tensor PCA
Jun 14, 2017
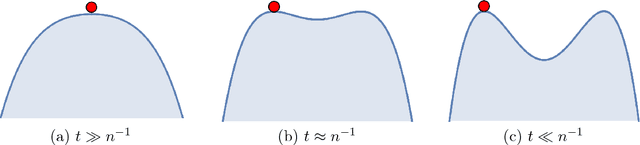
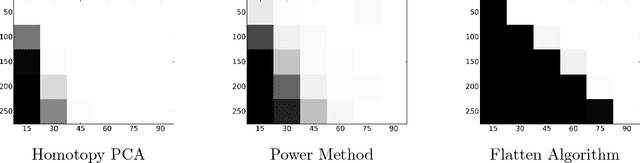
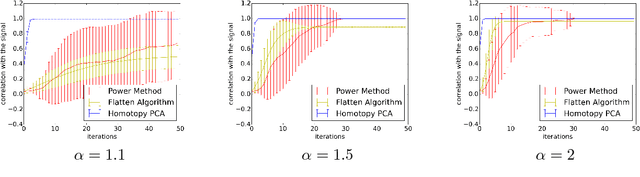
Abstract:Developing efficient and guaranteed nonconvex algorithms has been an important challenge in modern machine learning. Algorithms with good empirical performance such as stochastic gradient descent often lack theoretical guarantees. In this paper, we analyze the class of homotopy or continuation methods for global optimization of nonconvex functions. These methods start from an objective function that is efficient to optimize (e.g. convex), and progressively modify it to obtain the required objective, and the solutions are passed along the homotopy path. For the challenging problem of tensor PCA, we prove global convergence of the homotopy method in the "high noise" regime. The signal-to-noise requirement for our algorithm is tight in the sense that it matches the recovery guarantee for the best degree-4 sum-of-squares algorithm. In addition, we prove a phase transition along the homotopy path for tensor PCA. This allows to simplify the homotopy method to a local search algorithm, viz., tensor power iterations, with a specific initialization and a noise injection procedure, while retaining the theoretical guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge