Estimating the Influence of Sequentially Correlated Literary Properties in Textual Classification: A Data-Centric Hypothesis-Testing Approach

Stylometry aims to distinguish authors by analyzing literary traits assumed to reflect semi-conscious choices distinct from elements like genre or theme. However, these components often overlap, complicating text classification based solely on feature distributions. While some literary properties, such as thematic content, are likely to manifest as correlations between adjacent text units, others, like authorial style, may be independent thereof. We introduce a hypothesis-testing approach to evaluate the influence of sequentially correlated literary properties on text classification, aiming to determine when these correlations drive classification. Using a multivariate binary distribution, our method models sequential correlations between text units as a stochastic process, assessing the likelihood of clustering across varying adjacency scales. This enables us to examine whether classification is dominated by sequentially correlated properties or remains independent. In experiments on a diverse English prose corpus, our analysis integrates traditional and neural embeddings within supervised and unsupervised frameworks. Results demonstrate that our approach effectively identifies when textual classification is not primarily influenced by sequentially correlated literary properties, particularly in cases where texts differ in authorial style or genre rather than by a single author within a similar genre.

A Statistical Exploration of Text Partition Into Constituents: The Case of the Priestly Source in the Books of Genesis and Exodus

We present a pipeline for a statistical textual exploration, offering a stylometry-based explanation and statistical validation of a hypothesized partition of a text. Given a parameterization of the text, our pipeline: (1) detects literary features yielding the optimal overlap between the hypothesized and unsupervised partitions, (2) performs a hypothesis-testing analysis to quantify the statistical significance of the optimal overlap, while conserving implicit correlations between units of text that are more likely to be grouped, and (3) extracts and quantifies the importance of features most responsible for the classification, estimates their statistical stability and cluster-wise abundance. We apply our pipeline to the first two books in the Bible, where one stylistic component stands out in the eyes of biblical scholars, namely, the Priestly component. We identify and explore statistically significant stylistic differences between the Priestly and non-Priestly components.

Manifold Free Riemannian Optimization

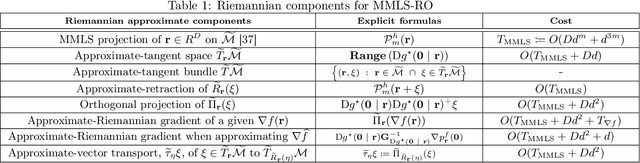
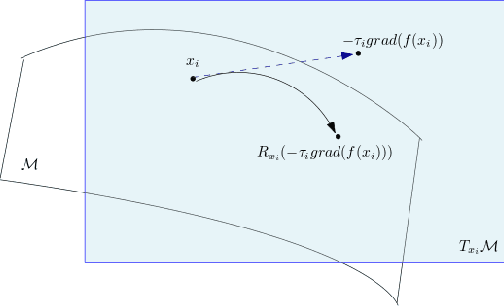
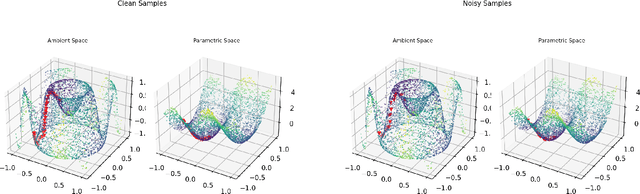
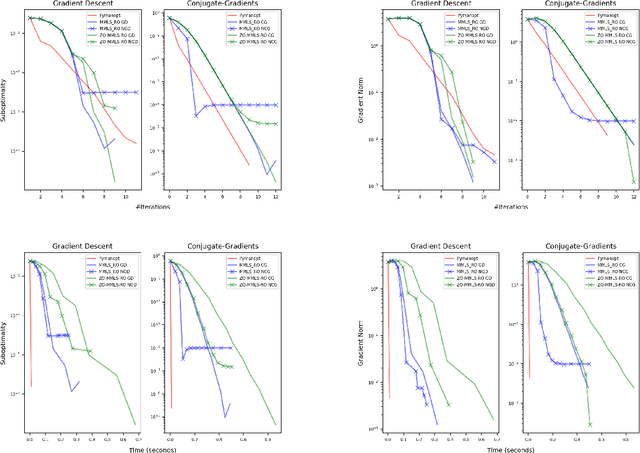
Riemannian optimization is a principled framework for solving optimization problems where the desired optimum is constrained to a smooth manifold $\mathcal{M}$. Algorithms designed in this framework usually require some geometrical description of the manifold, which typically includes tangent spaces, retractions, and gradients of the cost function. However, in many cases, only a subset (or none at all) of these elements can be accessed due to lack of information or intractability. In this paper, we propose a novel approach that can perform approximate Riemannian optimization in such cases, where the constraining manifold is a submanifold of $\R^{D}$. At the bare minimum, our method requires only a noiseless sample set of the cost function $(\x_{i}, y_{i})\in {\mathcal{M}} \times \mathbb{R}$ and the intrinsic dimension of the manifold $\mathcal{M}$. Using the samples, and utilizing the Manifold-MLS framework (Sober and Levin 2020), we construct approximations of the missing components entertaining provable guarantees and analyze their computational costs. In case some of the components are given analytically (e.g., if the cost function and its gradient are given explicitly, or if the tangent spaces can be computed), the algorithm can be easily adapted to use the accurate expressions instead of the approximations. We analyze the global convergence of Riemannian gradient-based methods using our approach, and we demonstrate empirically the strength of this method, together with a conjugate-gradients type method based upon similar principles.

Mixed X-Ray Image Separation for Artworks with Concealed Designs

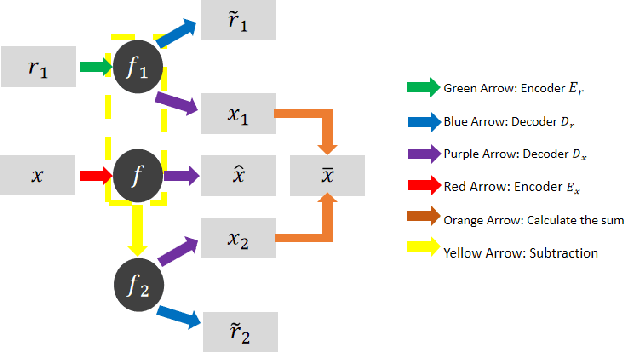
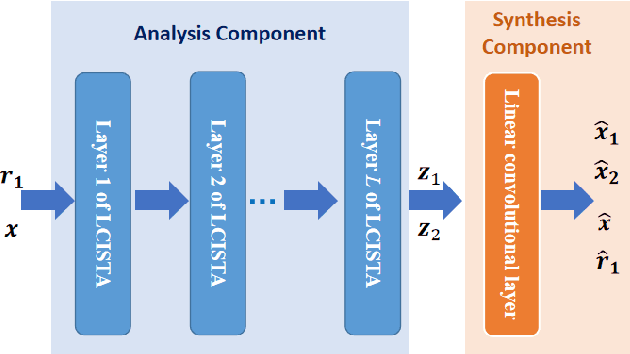
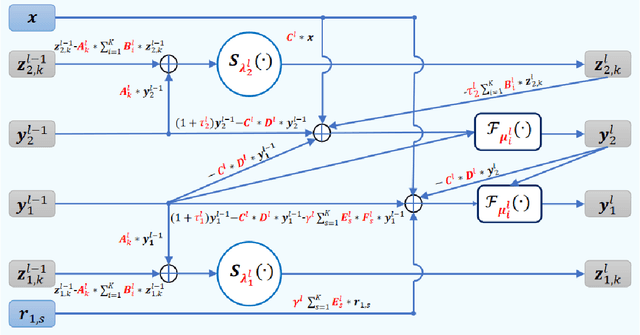
In this paper, we focus on X-ray images of paintings with concealed sub-surface designs (e.g., deriving from reuse of the painting support or revision of a composition by the artist), which include contributions from both the surface painting and the concealed features. In particular, we propose a self-supervised deep learning-based image separation approach that can be applied to the X-ray images from such paintings to separate them into two hypothetical X-ray images. One of these reconstructed images is related to the X-ray image of the concealed painting, while the second one contains only information related to the X-ray of the visible painting. The proposed separation network consists of two components: the analysis and the synthesis sub-networks. The analysis sub-network is based on learned coupled iterative shrinkage thresholding algorithms (LCISTA) designed using algorithm unrolling techniques, and the synthesis sub-network consists of several linear mappings. The learning algorithm operates in a totally self-supervised fashion without requiring a sample set that contains both the mixed X-ray images and the separated ones. The proposed method is demonstrated on a real painting with concealed content, Do\~na Isabel de Porcel by Francisco de Goya, to show its effectiveness.

Neural Network Approximation of Refinable Functions

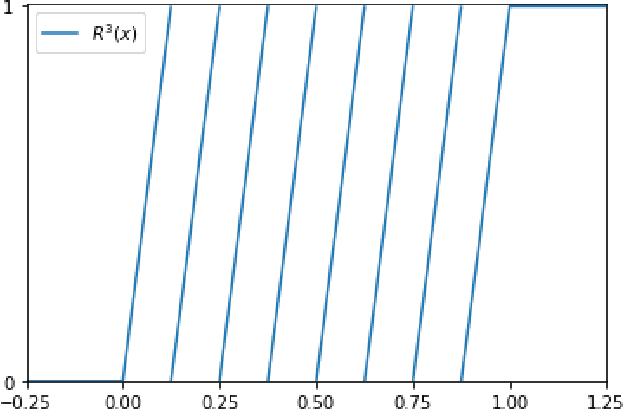
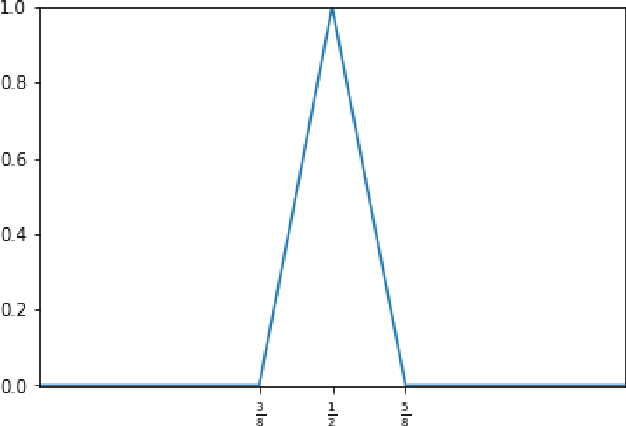
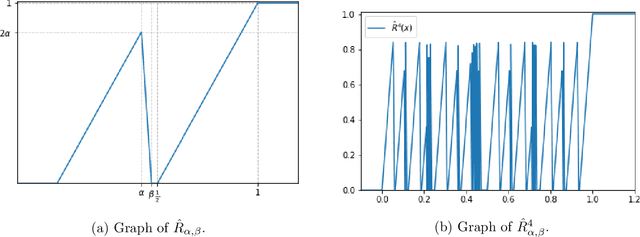
In the desire to quantify the success of neural networks in deep learning and other applications, there is a great interest in understanding which functions are efficiently approximated by the outputs of neural networks. By now, there exists a variety of results which show that a wide range of functions can be approximated with sometimes surprising accuracy by these outputs. For example, it is known that the set of functions that can be approximated with exponential accuracy (in terms of the number of parameters used) includes, on one hand, very smooth functions such as polynomials and analytic functions (see e.g. \cite{E,S,Y}) and, on the other hand, very rough functions such as the Weierstrass function (see e.g. \cite{EPGB,DDFHP}), which is nowhere differentiable. In this paper, we add to the latter class of rough functions by showing that it also includes refinable functions. Namely, we show that refinable functions are approximated by the outputs of deep ReLU networks with a fixed width and increasing depth with accuracy exponential in terms of their number of parameters. Our results apply to functions used in the standard construction of wavelets as well as to functions constructed via subdivision algorithms in Computer Aided Geometric Design.

Non-Parametric Estimation of Manifolds from Noisy Data

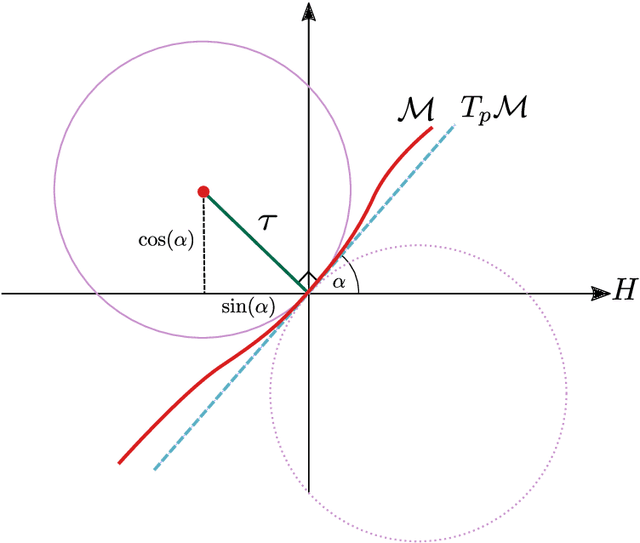
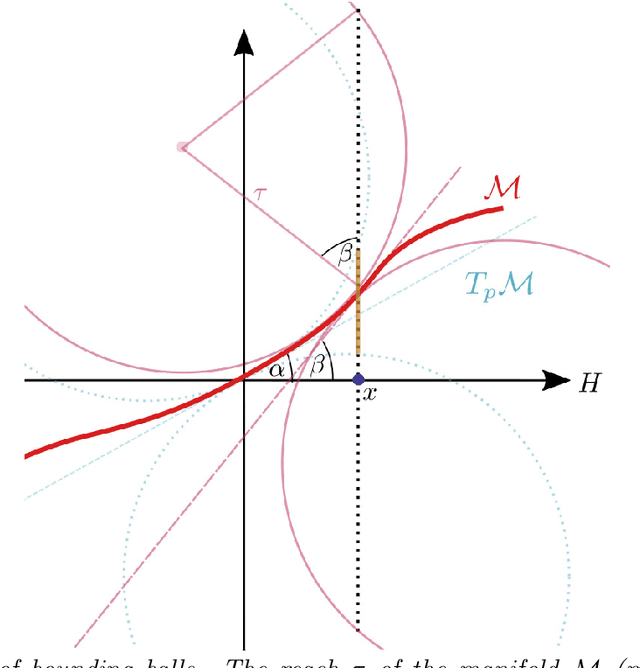
A common observation in data-driven applications is that high dimensional data has a low intrinsic dimension, at least locally. In this work, we consider the problem of estimating a $d$ dimensional sub-manifold of $\mathbb{R}^D$ from a finite set of noisy samples. Assuming that the data was sampled uniformly from a tubular neighborhood of $\mathcal{M}\in \mathcal{C}^k$, a compact manifold without boundary, we present an algorithm that takes a point $r$ from the tubular neighborhood and outputs $\hat p_n\in \mathbb{R}^D$, and $\widehat{T_{\hat p_n}\mathcal{M}}$ an element in the Grassmanian $Gr(d, D)$. We prove that as the number of samples $n\to\infty$ the point $\hat p_n$ converges to $p\in \mathcal{M}$ and $\widehat{T_{\hat p_n}\mathcal{M}}$ converges to $T_p\mathcal{M}$ (the tangent space at that point) with high probability. Furthermore, we show that the estimation yields asymptotic rates of convergence of $n^{-\frac{k}{2k + d}}$ for the point estimation and $n^{-\frac{k-1}{2k + d}}$ for the estimation of the tangent space. These rates are known to be optimal for the case of function estimation.

Image Separation with Side Information: A Connected Auto-Encoders Based Approach

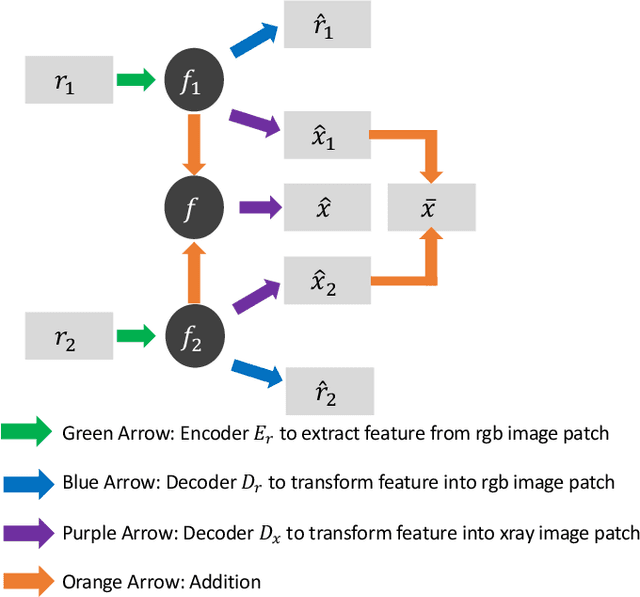
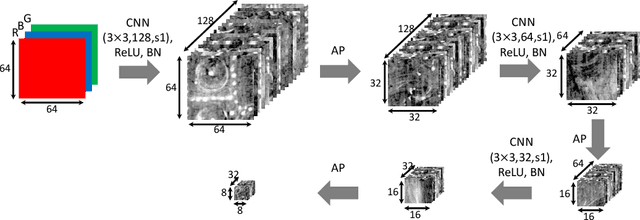
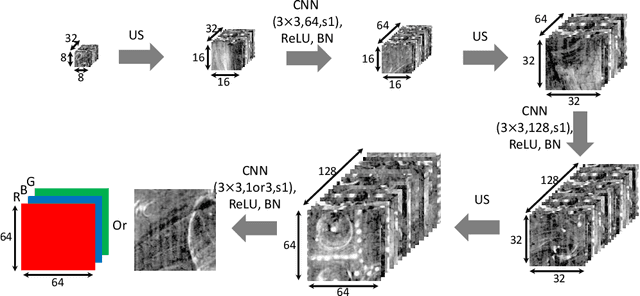
X-radiography (X-ray imaging) is a widely used imaging technique in art investigation. It can provide information about the condition of a painting as well as insights into an artist's techniques and working methods, often revealing hidden information invisible to the naked eye. In this paper, we deal with the problem of separating mixed X-ray images originating from the radiography of double-sided paintings. Using the visible color images (RGB images) from each side of the painting, we propose a new Neural Network architecture, based upon 'connected' auto-encoders, designed to separate the mixed X-ray image into two simulated X-ray images corresponding to each side. In this proposed architecture, the convolutional auto encoders extract features from the RGB images. These features are then used to (1) reproduce both of the original RGB images, (2) reconstruct the hypothetical separated X-ray images, and (3) regenerate the mixed X-ray image. The algorithm operates in a totally self-supervised fashion without requiring a sample set that contains both the mixed X-ray images and the separated ones. The methodology was tested on images from the double-sided wing panels of the \textsl{Ghent Altarpiece}, painted in 1432 by the brothers Hubert and Jan van Eyck. These tests show that the proposed approach outperforms other state-of-the-art X-ray image separation methods for art investigation applications.

Approximating the Riemannian Metric from Point Clouds via Manifold Moving Least Squares

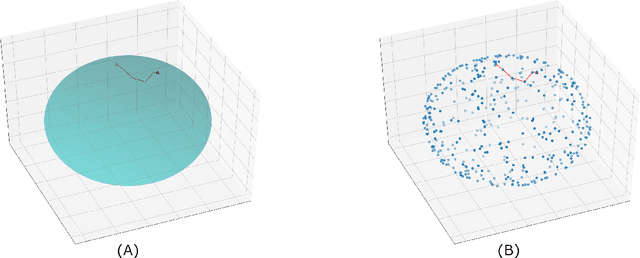
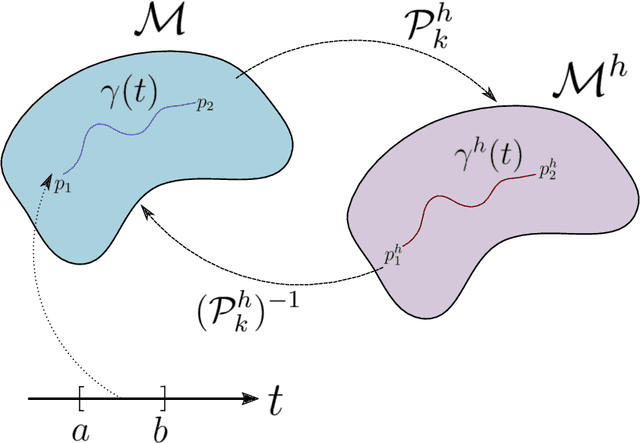
The approximation of both geodesic distances and shortest paths on point cloud sampled from an embedded submanifold $\mathcal{M}$ of Euclidean space has been a long-standing challenge in computational geometry. Given a sampling resolution parameter $ h $, state-of-the-art discrete methods yield $ O(h^2) $ approximations at most. In this paper, we investigate the convergence of such approximations made by Manifold Moving Least-Squares (Manifold-MLS), a method that constructs an approximating manifold $\mathcal{M}^h$ using information from a given point cloud that was developed by Sober \& Levin in 2019 . They showed that the Manifold-MLS procedure approximates the original manifold with approximation order of $ O(h^{k})$ provided that the original manifold $\mathcal{M} \in C^{k}$ is closed, i.e. $\mathcal{M}$ is a compact manifold without boundary. In this paper, we show that under the same conditions, the Riemannian metric of $ \mathcal{M}^h $ approximates the Riemannian metric of $ \mathcal{M}, $; i.e., $\mathcal{M}$ is nearly isometric to $\mathcal{M}^h$. Explicitly, given points $ p_1, p_2 \in \mathcal{M} $ with geodesic distance $ \rho_{\mathcal{M}}(p_1, p_2) $, we show that their corresponding points $ p_1^h, p_2^h \in \mathcal{M}^h $ have a geodesic distance of $ \rho_{\mathcal{M}^h}(p_1^h,p_2^h) = \rho_{\mathcal{M}}(p_1, p_2) + O(h^{k-1}) $. We then use this result, as well as the fact that $ \mathcal{M}^h $ can be sampled with any desired resolution, to devise a naive algorithm that yields approximate geodesic distances with rate of convergence $ O(h^{k-1}) $. We show the potential and the robustness to noise of the proposed method on some numerical simulations.

Expression of Fractals Through Neural Network Functions

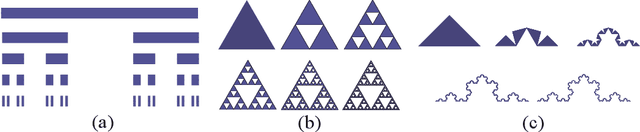
To help understand the underlying mechanisms of neural networks (NNs), several groups have, in recent years, studied the number of linear regions $\ell$ of piecewise linear functions generated by deep neural networks (DNN). In particular, they showed that $\ell$ can grow exponentially with the number of network parameters $p$, a property often used to explain the advantages of DNNs over shallow NNs in approximating complicated functions. Nonetheless, a simple dimension argument shows that DNNs cannot generate all piecewise linear functions with $\ell$ linear regions as soon as $\ell > p$. It is thus natural to seek to characterize specific families of functions with $\ell$ linear regions that can be constructed by DNNs. Iterated Function Systems (IFS) generate sequences of piecewise linear functions $F_k$ with a number of linear regions exponential in $k$. We show that, under mild assumptions, $F_k$ can be generated by a NN using only $\mathcal{O}(k)$ parameters. IFS are used extensively to generate, at low computational cost, natural-looking landscape textures in artificial images. They have also been proposed for compression of natural images, albeit with less commercial success. The surprisingly good performance of this fractal-based compression suggests that our visual system may lock in, to some extent, on self-similarities in images. The combination of this phenomenon with the capacity, demonstrated here, of DNNs to efficiently approximate IFS may contribute to the success of DNNs, particularly striking for image processing tasks, as well as suggest new algorithms for representing self similarities in images based on the DNN mechanism.

Approximation of Functions over Manifolds: A Moving Least-Squares Approach

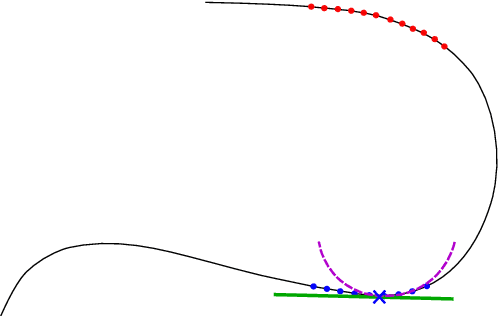
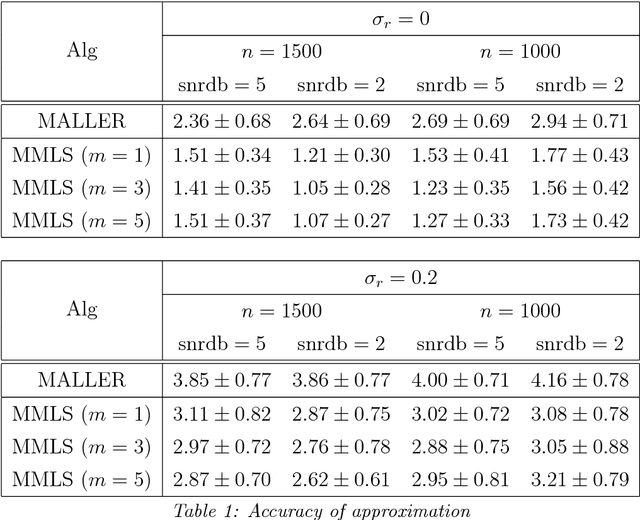
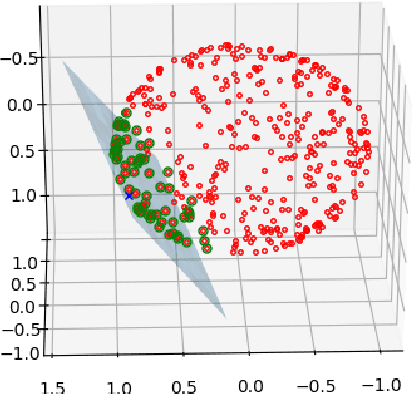
We present an algorithm for approximating a function defined over a $d$-dimensional manifold utilizing only noisy function values at locations sampled from the manifold with noise. To produce the approximation we do not require any knowledge regarding the manifold other than its dimension $d$. The approximation scheme is based upon the Manifold Moving Least-Squares (MMLS). The proposed algorithm is resistant to noise in both the domain and function values. Furthermore, the approximant is shown to be smooth and of approximation order of $\mathcal{O}(h^{m+1})$ for non-noisy data, where $h$ is the mesh size with respect to the manifold domain, and $m$ is the degree of a local polynomial approximation utilized in our algorithm. In addition, the proposed algorithm is linear in time with respect to the ambient-space's dimension. Thus, in case of extremely large ambient space dimension, we are able to avoid the curse of dimensionality without having to perform non-linear dimension reduction, which introduces distortions to the manifold data. Using numerical experiments, we compare the presented method to state-of-the-art algorithms for regression over manifolds and show its potential.