Low-rank data modeling via the Minimum Description Length principle

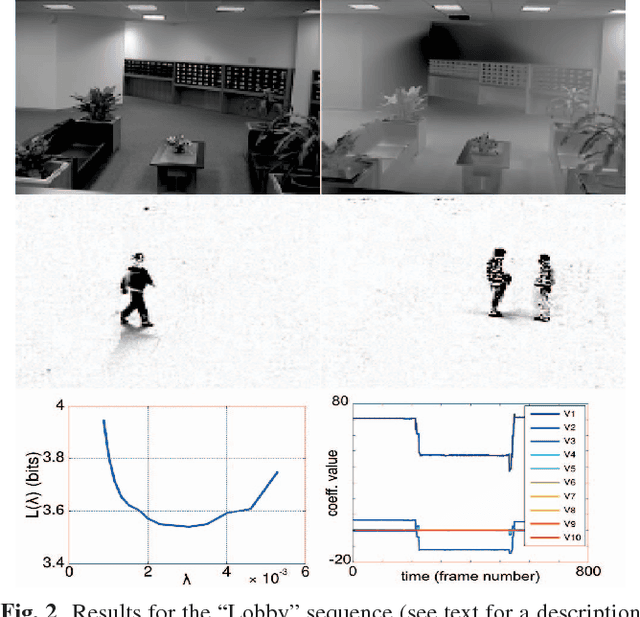
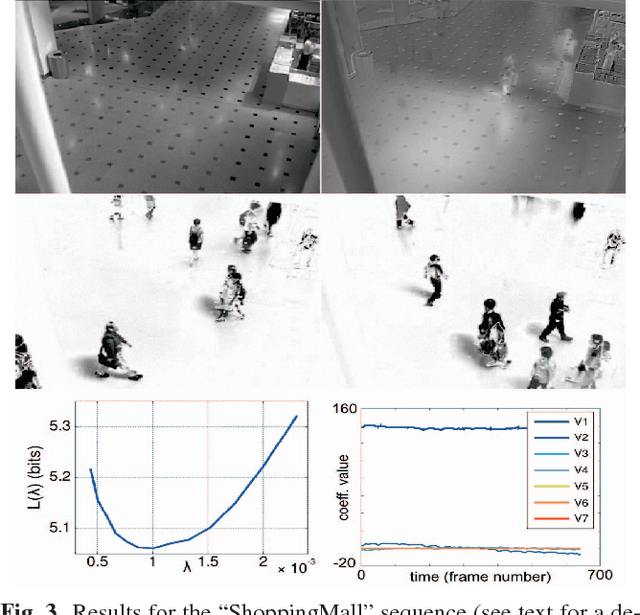
Robust low-rank matrix estimation is a topic of increasing interest, with promising applications in a variety of fields, from computer vision to data mining and recommender systems. Recent theoretical results establish the ability of such data models to recover the true underlying low-rank matrix when a large portion of the measured matrix is either missing or arbitrarily corrupted. However, if low rank is not a hypothesis about the true nature of the data, but a device for extracting regularity from it, no current guidelines exist for choosing the rank of the estimated matrix. In this work we address this problem by means of the Minimum Description Length (MDL) principle -- a well established information-theoretic approach to statistical inference -- as a guideline for selecting a model for the data at hand. We demonstrate the practical usefulness of our formal approach with results for complex background extraction in video sequences.

C-HiLasso: A Collaborative Hierarchical Sparse Modeling Framework

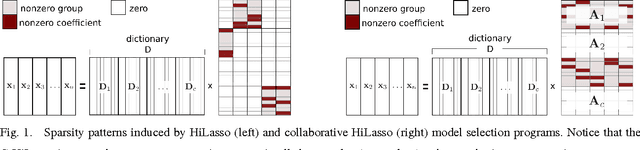
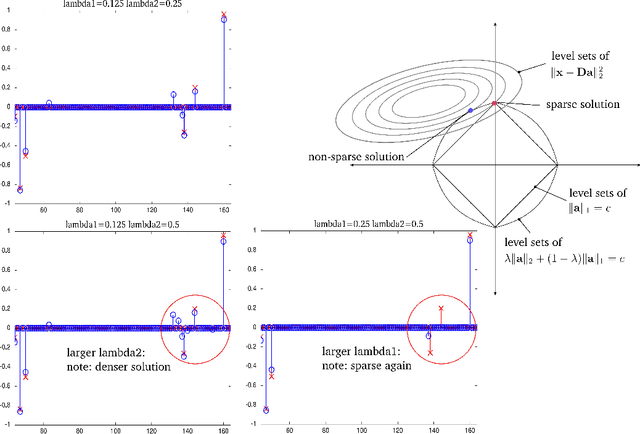
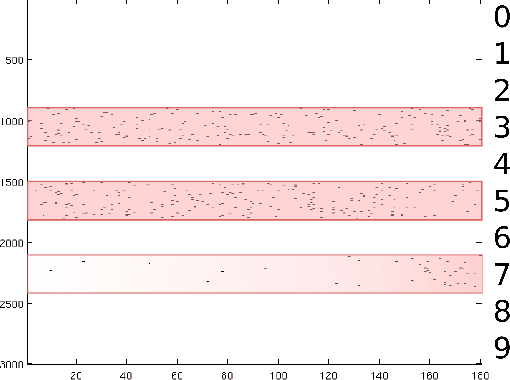
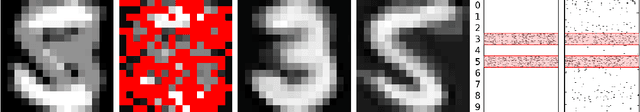
Sparse modeling is a powerful framework for data analysis and processing. Traditionally, encoding in this framework is performed by solving an L1-regularized linear regression problem, commonly referred to as Lasso or Basis Pursuit. In this work we combine the sparsity-inducing property of the Lasso model at the individual feature level, with the block-sparsity property of the Group Lasso model, where sparse groups of features are jointly encoded, obtaining a sparsity pattern hierarchically structured. This results in the Hierarchical Lasso (HiLasso), which shows important practical modeling advantages. We then extend this approach to the collaborative case, where a set of simultaneously coded signals share the same sparsity pattern at the higher (group) level, but not necessarily at the lower (inside the group) level, obtaining the collaborative HiLasso model (C-HiLasso). Such signals then share the same active groups, or classes, but not necessarily the same active set. This model is very well suited for applications such as source identification and separation. An efficient optimization procedure, which guarantees convergence to the global optimum, is developed for these new models. The underlying presentation of the new framework and optimization approach is complemented with experimental examples and theoretical results regarding recovery guarantees for the proposed models.

A convex model for non-negative matrix factorization and dimensionality reduction on physical space

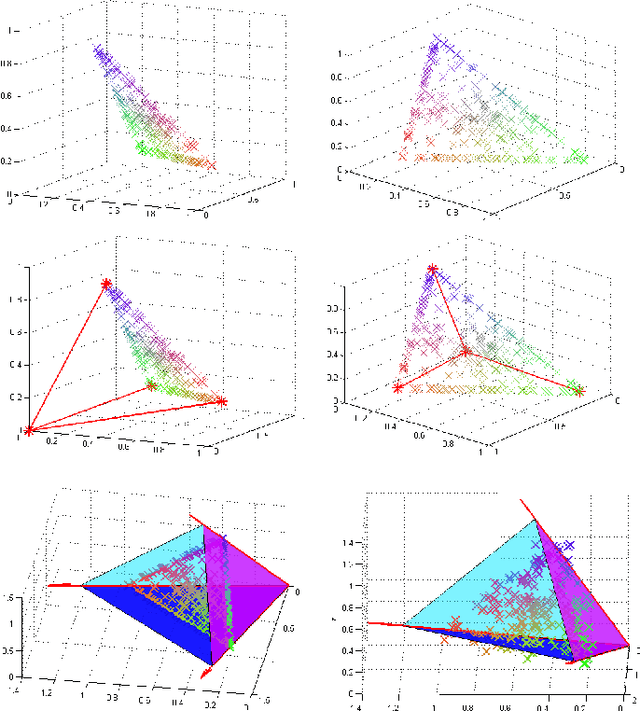
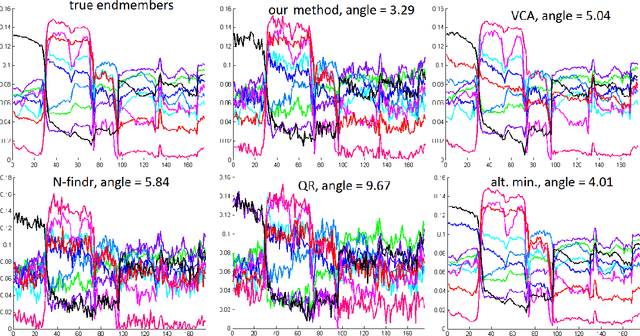
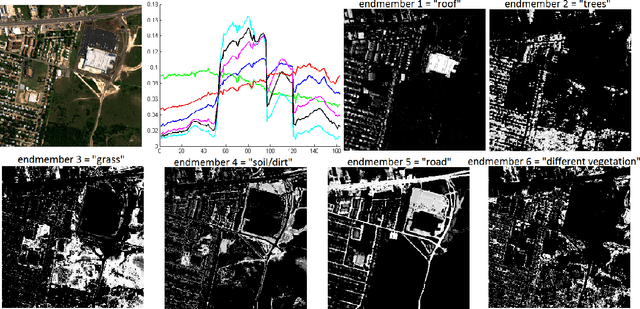
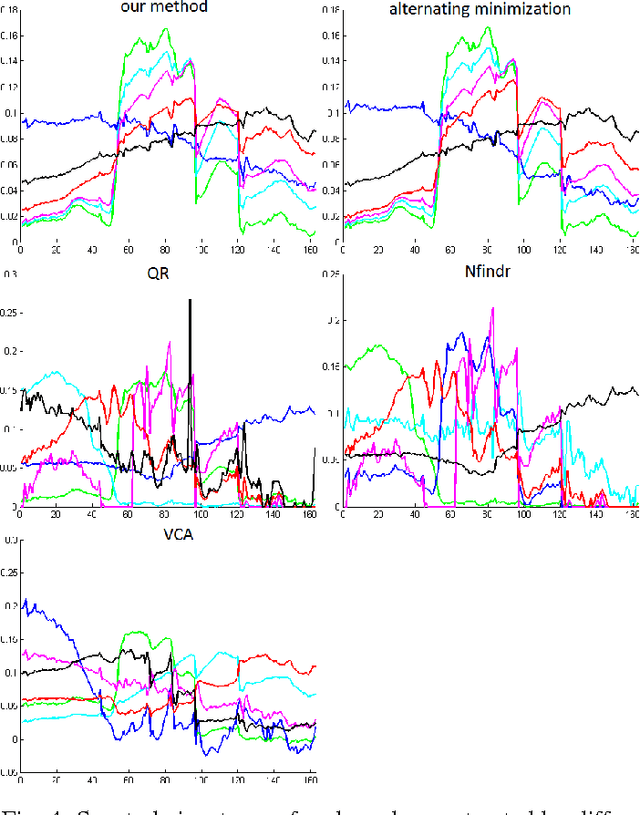
A collaborative convex framework for factoring a data matrix $X$ into a non-negative product $AS$, with a sparse coefficient matrix $S$, is proposed. We restrict the columns of the dictionary matrix $A$ to coincide with certain columns of the data matrix $X$, thereby guaranteeing a physically meaningful dictionary and dimensionality reduction. We use $l_{1,\infty}$ regularization to select the dictionary from the data and show this leads to an exact convex relaxation of $l_0$ in the case of distinct noise free data. We also show how to relax the restriction-to-$X$ constraint by initializing an alternating minimization approach with the solution of the convex model, obtaining a dictionary close to but not necessarily in $X$. We focus on applications of the proposed framework to hyperspectral endmember and abundances identification and also show an application to blind source separation of NMR data.

Statistical Compressed Sensing of Gaussian Mixture Models

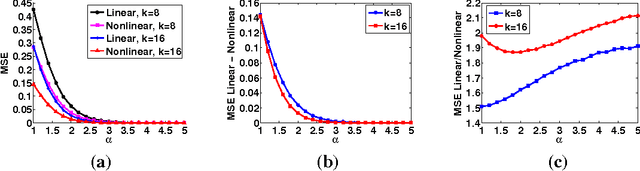
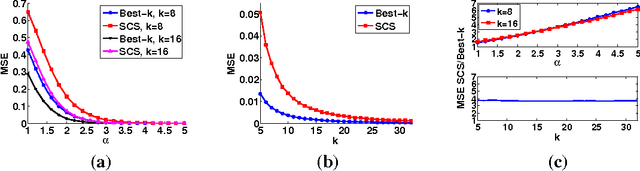
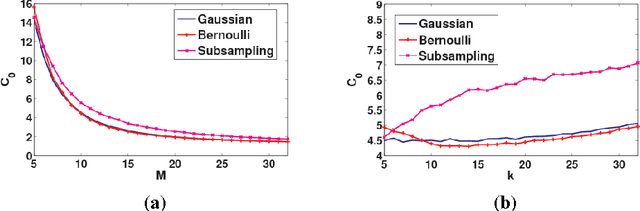
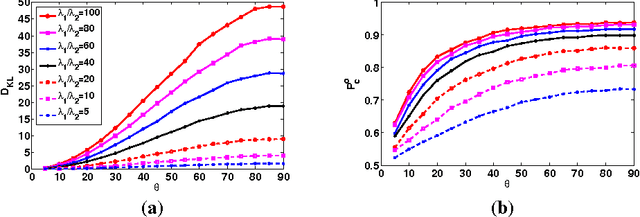
A novel framework of compressed sensing, namely statistical compressed sensing (SCS), that aims at efficiently sampling a collection of signals that follow a statistical distribution, and achieving accurate reconstruction on average, is introduced. SCS based on Gaussian models is investigated in depth. For signals that follow a single Gaussian model, with Gaussian or Bernoulli sensing matrices of O(k) measurements, considerably smaller than the O(k log(N/k)) required by conventional CS based on sparse models, where N is the signal dimension, and with an optimal decoder implemented via linear filtering, significantly faster than the pursuit decoders applied in conventional CS, the error of SCS is shown tightly upper bounded by a constant times the best k-term approximation error, with overwhelming probability. The failure probability is also significantly smaller than that of conventional sparsity-oriented CS. Stronger yet simpler results further show that for any sensing matrix, the error of Gaussian SCS is upper bounded by a constant times the best k-term approximation with probability one, and the bound constant can be efficiently calculated. For Gaussian mixture models (GMMs), that assume multiple Gaussian distributions and that each signal follows one of them with an unknown index, a piecewise linear estimator is introduced to decode SCS. The accuracy of model selection, at the heart of the piecewise linear decoder, is analyzed in terms of the properties of the Gaussian distributions and the number of sensing measurements. A maximum a posteriori expectation-maximization algorithm that iteratively estimates the Gaussian models parameters, the signals model selection, and decodes the signals, is presented for GMM-based SCS. In real image sensing applications, GMM-based SCS is shown to lead to improved results compared to conventional CS, at a considerably lower computational cost.

Collaborative Sources Identification in Mixed Signals via Hierarchical Sparse Modeling

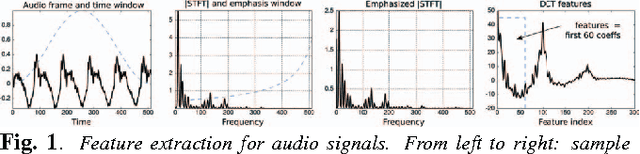
A collaborative framework for detecting the different sources in mixed signals is presented in this paper. The approach is based on C-HiLasso, a convex collaborative hierarchical sparse model, and proceeds as follows. First, we build a structured dictionary for mixed signals by concatenating a set of sub-dictionaries, each one of them learned to sparsely model one of a set of possible classes. Then, the coding of the mixed signal is performed by efficiently solving a convex optimization problem that combines standard sparsity with group and collaborative sparsity. The present sources are identified by looking at the sub-dictionaries automatically selected in the coding. The collaborative filtering in C-HiLasso takes advantage of the temporal/spatial redundancy in the mixed signals, letting collections of samples collaborate in identifying the classes, while allowing individual samples to have different internal sparse representations. This collaboration is critical to further stabilize the sparse representation of signals, in particular the class/sub-dictionary selection. The internal sparsity inside the sub-dictionaries, as naturally incorporated by the hierarchical aspects of C-HiLasso, is critical to make the model consistent with the essence of the sub-dictionaries that have been trained for sparse representation of each individual class. We present applications from speaker and instrument identification and texture separation. In the case of audio signals, we use sparse modeling to describe the short-term power spectrum envelopes of harmonic sounds. The proposed pitch independent method automatically detects the number of sources on a recording.

Statistical Compressive Sensing of Gaussian Mixture Models

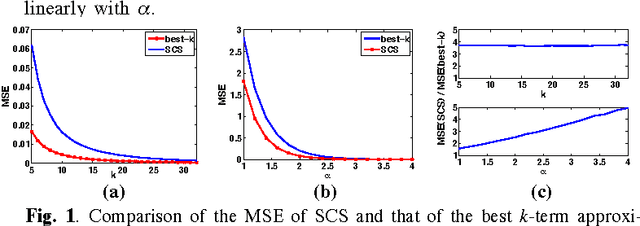
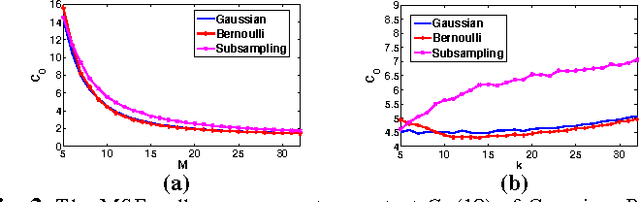
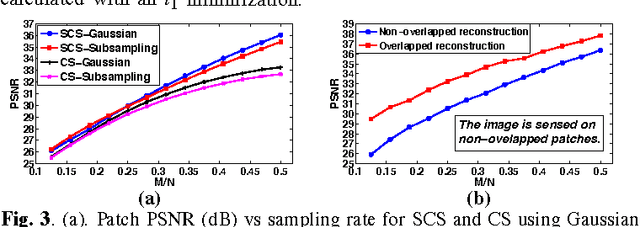
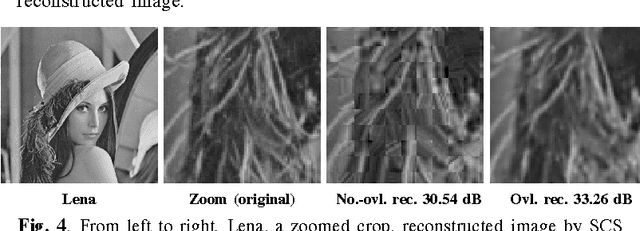
A new framework of compressive sensing (CS), namely statistical compressive sensing (SCS), that aims at efficiently sampling a collection of signals that follow a statistical distribution and achieving accurate reconstruction on average, is introduced. For signals following a Gaussian distribution, with Gaussian or Bernoulli sensing matrices of O(k) measurements, considerably smaller than the O(k log(N/k)) required by conventional CS, where N is the signal dimension, and with an optimal decoder implemented with linear filtering, significantly faster than the pursuit decoders applied in conventional CS, the error of SCS is shown tightly upper bounded by a constant times the k-best term approximation error, with overwhelming probability. The failure probability is also significantly smaller than that of conventional CS. Stronger yet simpler results further show that for any sensing matrix, the error of Gaussian SCS is upper bounded by a constant times the k-best term approximation with probability one, and the bound constant can be efficiently calculated. For signals following Gaussian mixture models, SCS with a piecewise linear decoder is introduced and shown to produce for real images better results than conventional CS based on sparse models.

Efficient Matrix Completion with Gaussian Models

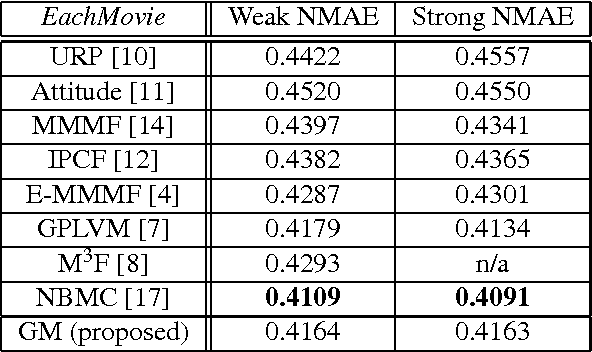
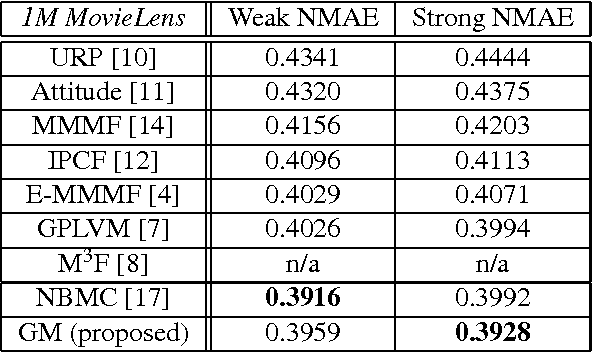
A general framework based on Gaussian models and a MAP-EM algorithm is introduced in this paper for solving matrix/table completion problems. The numerical experiments with the standard and challenging movie ratings data show that the proposed approach, based on probably one of the simplest probabilistic models, leads to the results in the same ballpark as the state-of-the-art, at a lower computational cost.

Universal Regularizers For Robust Sparse Coding and Modeling

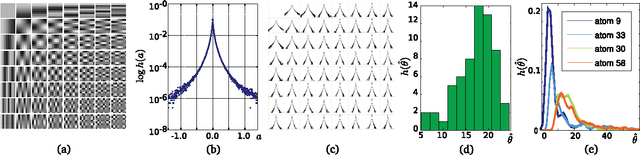
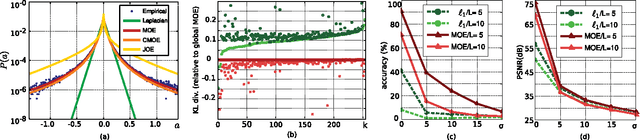
Sparse data models, where data is assumed to be well represented as a linear combination of a few elements from a dictionary, have gained considerable attention in recent years, and their use has led to state-of-the-art results in many signal and image processing tasks. It is now well understood that the choice of the sparsity regularization term is critical in the success of such models. Based on a codelength minimization interpretation of sparse coding, and using tools from universal coding theory, we propose a framework for designing sparsity regularization terms which have theoretical and practical advantages when compared to the more standard l0 or l1 ones. The presentation of the framework and theoretical foundations is complemented with examples that show its practical advantages in image denoising, zooming and classification.

Solving Inverse Problems with Piecewise Linear Estimators: From Gaussian Mixture Models to Structured Sparsity

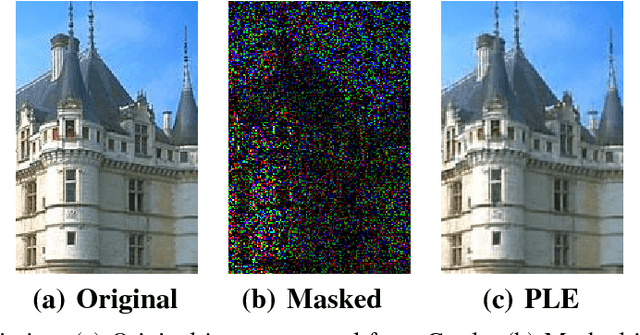
A general framework for solving image inverse problems is introduced in this paper. The approach is based on Gaussian mixture models, estimated via a computationally efficient MAP-EM algorithm. A dual mathematical interpretation of the proposed framework with structured sparse estimation is described, which shows that the resulting piecewise linear estimate stabilizes the estimation when compared to traditional sparse inverse problem techniques. This interpretation also suggests an effective dictionary motivated initialization for the MAP-EM algorithm. We demonstrate that in a number of image inverse problems, including inpainting, zooming, and deblurring, the same algorithm produces either equal, often significantly better, or very small margin worse results than the best published ones, at a lower computational cost.

Online Learning for Matrix Factorization and Sparse Coding

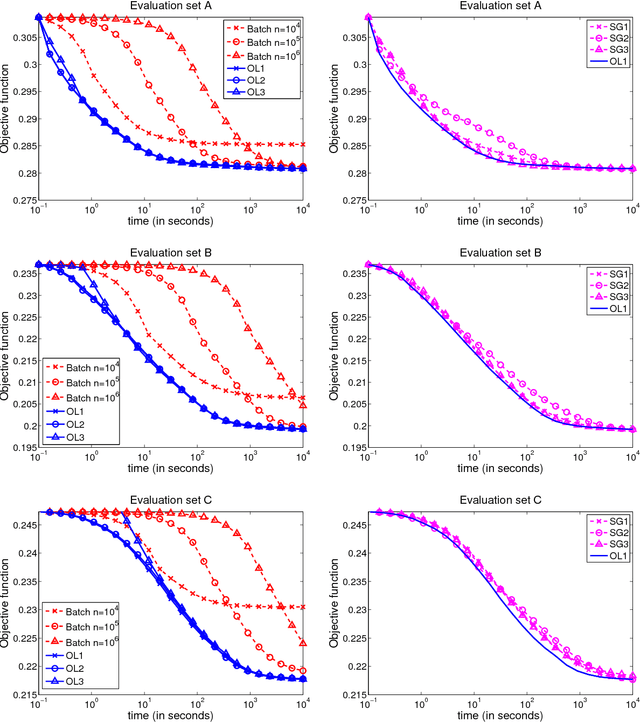
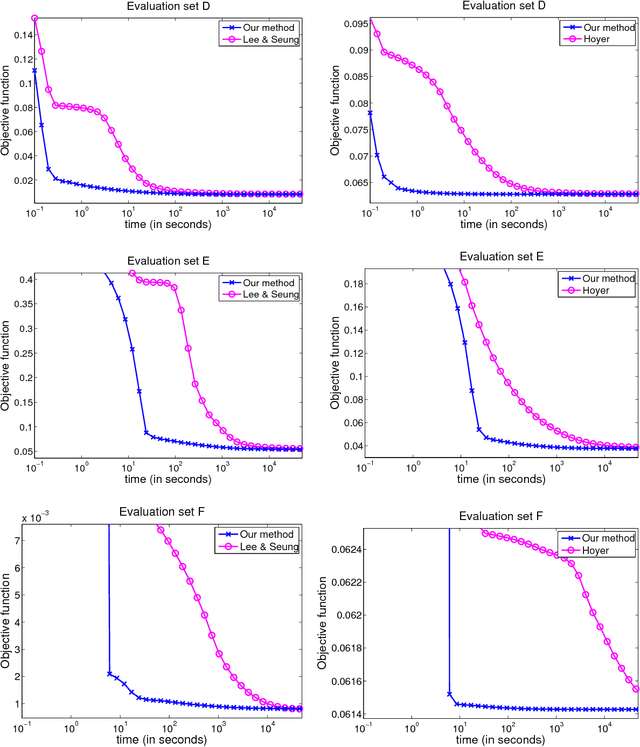
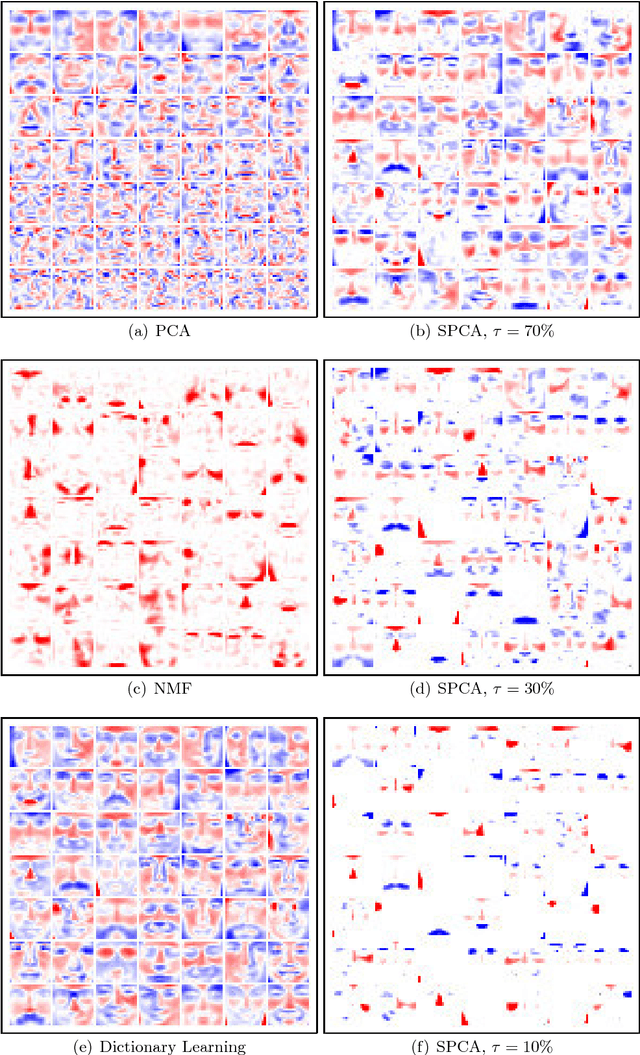
Sparse coding--that is, modelling data vectors as sparse linear combinations of basis elements--is widely used in machine learning, neuroscience, signal processing, and statistics. This paper focuses on the large-scale matrix factorization problem that consists of learning the basis set, adapting it to specific data. Variations of this problem include dictionary learning in signal processing, non-negative matrix factorization and sparse principal component analysis. In this paper, we propose to address these tasks with a new online optimization algorithm, based on stochastic approximations, which scales up gracefully to large datasets with millions of training samples, and extends naturally to various matrix factorization formulations, making it suitable for a wide range of learning problems. A proof of convergence is presented, along with experiments with natural images and genomic data demonstrating that it leads to state-of-the-art performance in terms of speed and optimization for both small and large datasets.