Binary Matrix Factorization via Dictionary Learning

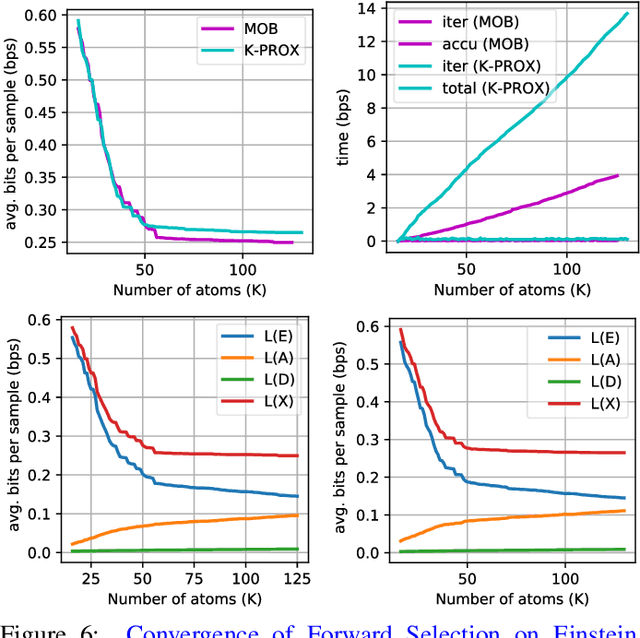
Matrix factorization is a key tool in data analysis; its applications include recommender systems, correlation analysis, signal processing, among others. Binary matrices are a particular case which has received significant attention for over thirty years, especially within the field of data mining. Dictionary learning refers to a family of methods for learning overcomplete basis (also called frames) in order to efficiently encode samples of a given type; this area, now also about twenty years old, was mostly developed within the signal processing field. In this work we propose two binary matrix factorization methods based on a binary adaptation of the dictionary learning paradigm to binary matrices. The proposed algorithms focus on speed and scalability; they work with binary factors combined with bit-wise operations and a few auxiliary integer ones. Furthermore, the methods are readily applicable to online binary matrix factorization. Another important issue in matrix factorization is the choice of rank for the factors; we address this model selection problem with an efficient method based on the Minimum Description Length principle. Our preliminary results show that the proposed methods are effective at producing interpretable factorizations of various data types of different nature.

Collaborative Sources Identification in Mixed Signals via Hierarchical Sparse Modeling

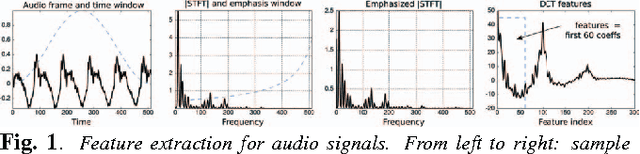
A collaborative framework for detecting the different sources in mixed signals is presented in this paper. The approach is based on C-HiLasso, a convex collaborative hierarchical sparse model, and proceeds as follows. First, we build a structured dictionary for mixed signals by concatenating a set of sub-dictionaries, each one of them learned to sparsely model one of a set of possible classes. Then, the coding of the mixed signal is performed by efficiently solving a convex optimization problem that combines standard sparsity with group and collaborative sparsity. The present sources are identified by looking at the sub-dictionaries automatically selected in the coding. The collaborative filtering in C-HiLasso takes advantage of the temporal/spatial redundancy in the mixed signals, letting collections of samples collaborate in identifying the classes, while allowing individual samples to have different internal sparse representations. This collaboration is critical to further stabilize the sparse representation of signals, in particular the class/sub-dictionary selection. The internal sparsity inside the sub-dictionaries, as naturally incorporated by the hierarchical aspects of C-HiLasso, is critical to make the model consistent with the essence of the sub-dictionaries that have been trained for sparse representation of each individual class. We present applications from speaker and instrument identification and texture separation. In the case of audio signals, we use sparse modeling to describe the short-term power spectrum envelopes of harmonic sounds. The proposed pitch independent method automatically detects the number of sources on a recording.

Universal Regularizers For Robust Sparse Coding and Modeling

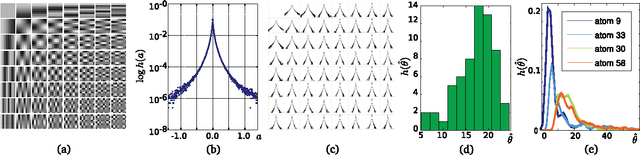
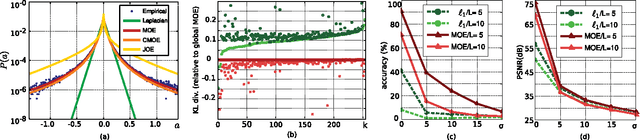
Sparse data models, where data is assumed to be well represented as a linear combination of a few elements from a dictionary, have gained considerable attention in recent years, and their use has led to state-of-the-art results in many signal and image processing tasks. It is now well understood that the choice of the sparsity regularization term is critical in the success of such models. Based on a codelength minimization interpretation of sparse coding, and using tools from universal coding theory, we propose a framework for designing sparsity regularization terms which have theoretical and practical advantages when compared to the more standard l0 or l1 ones. The presentation of the framework and theoretical foundations is complemented with examples that show its practical advantages in image denoising, zooming and classification.