Self-learning Scene-specific Pedestrian Detectors using a Progressive Latent Model

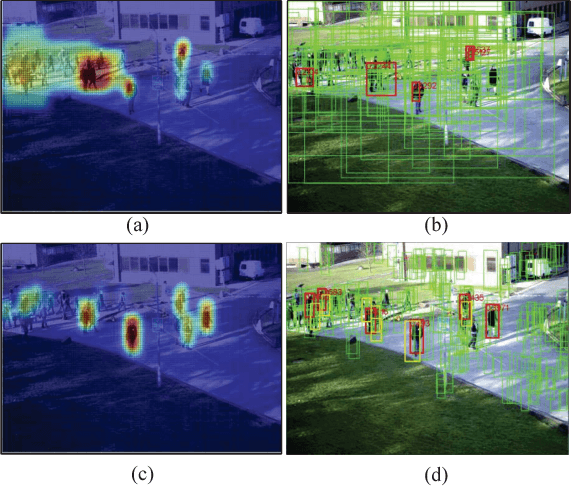
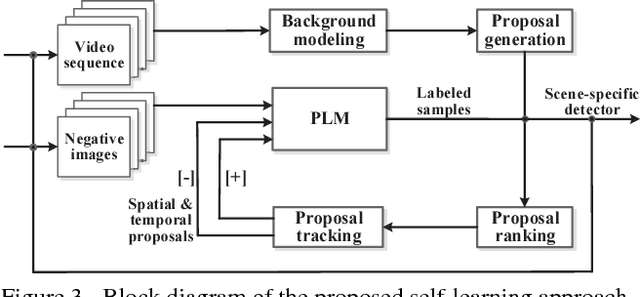
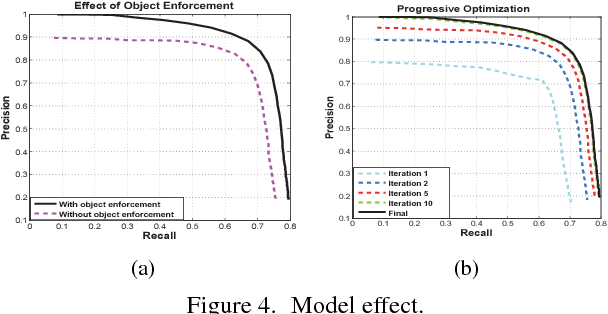
In this paper, a self-learning approach is proposed towards solving scene-specific pedestrian detection problem without any human' annotation involved. The self-learning approach is deployed as progressive steps of object discovery, object enforcement, and label propagation. In the learning procedure, object locations in each frame are treated as latent variables that are solved with a progressive latent model (PLM). Compared with conventional latent models, the proposed PLM incorporates a spatial regularization term to reduce ambiguities in object proposals and to enforce object localization, and also a graph-based label propagation to discover harder instances in adjacent frames. With the difference of convex (DC) objective functions, PLM can be efficiently optimized with a concave-convex programming and thus guaranteeing the stability of self-learning. Extensive experiments demonstrate that even without annotation the proposed self-learning approach outperforms weakly supervised learning approaches, while achieving comparable performance with transfer learning and fully supervised approaches.

Not Afraid of the Dark: NIR-VIS Face Recognition via Cross-spectral Hallucination and Low-rank Embedding

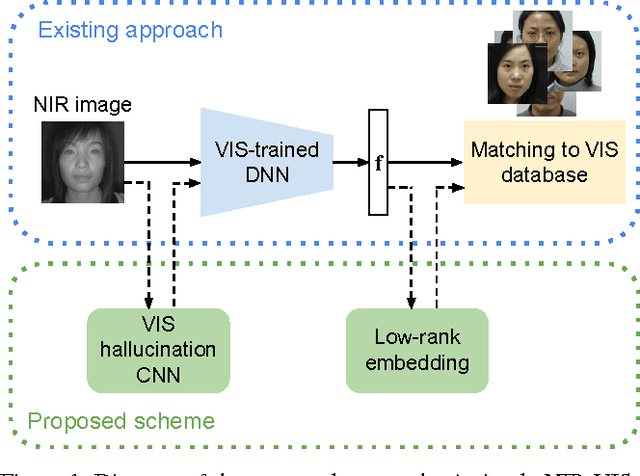
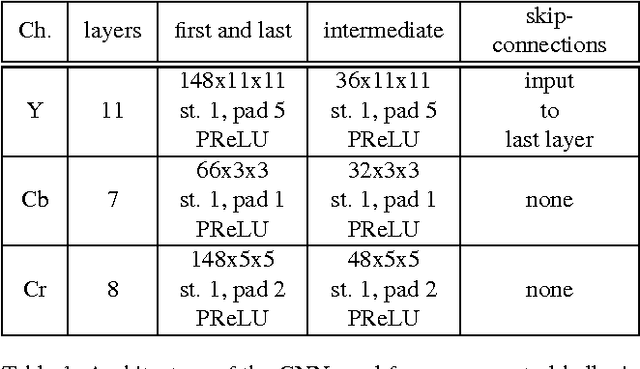
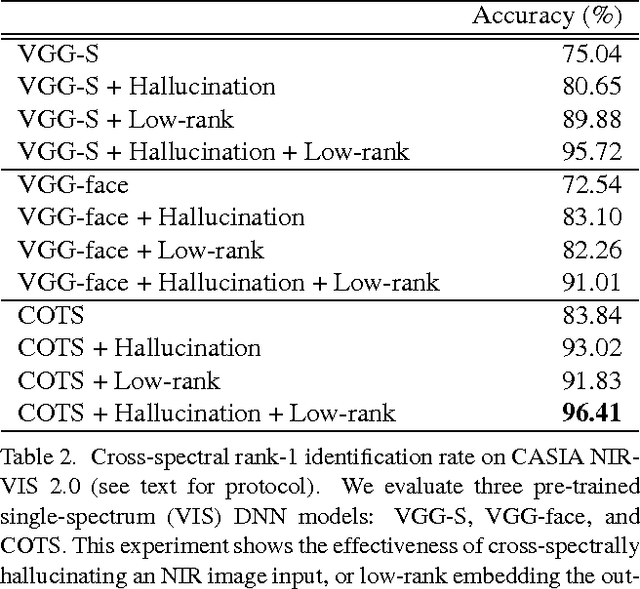
Surveillance cameras today often capture NIR (near infrared) images in low-light environments. However, most face datasets accessible for training and verification are only collected in the VIS (visible light) spectrum. It remains a challenging problem to match NIR to VIS face images due to the different light spectrum. Recently, breakthroughs have been made for VIS face recognition by applying deep learning on a huge amount of labeled VIS face samples. The same deep learning approach cannot be simply applied to NIR face recognition for two main reasons: First, much limited NIR face images are available for training compared to the VIS spectrum. Second, face galleries to be matched are mostly available only in the VIS spectrum. In this paper, we propose an approach to extend the deep learning breakthrough for VIS face recognition to the NIR spectrum, without retraining the underlying deep models that see only VIS faces. Our approach consists of two core components, cross-spectral hallucination and low-rank embedding, to optimize respectively input and output of a VIS deep model for cross-spectral face recognition. Cross-spectral hallucination produces VIS faces from NIR images through a deep learning approach. Low-rank embedding restores a low-rank structure for faces deep features across both NIR and VIS spectrum. We observe that it is often equally effective to perform hallucination to input NIR images or low-rank embedding to output deep features for a VIS deep model for cross-spectral recognition. When hallucination and low-rank embedding are deployed together, we observe significant further improvement; we obtain state-of-the-art accuracy on the CASIA NIR-VIS v2.0 benchmark, without the need at all to re-train the recognition system.

Probabilistic Fluorescence-Based Synapse Detection

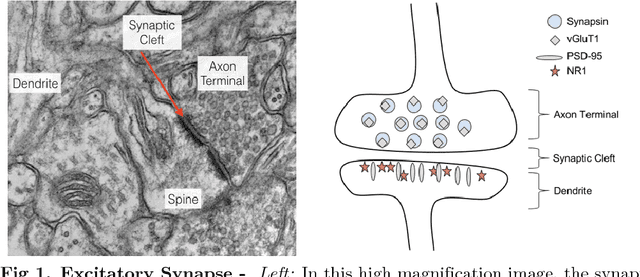
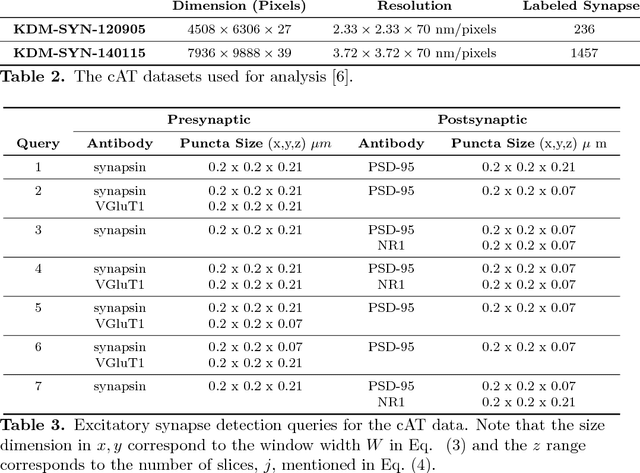
Brain function results from communication between neurons connected by complex synaptic networks. Synapses are themselves highly complex and diverse signaling machines, containing protein products of hundreds of different genes, some in hundreds of copies, arranged in precise lattice at each individual synapse. Synapses are fundamental not only to synaptic network function but also to network development, adaptation, and memory. In addition, abnormalities of synapse numbers or molecular components are implicated in most mental and neurological disorders. Despite their obvious importance, mammalian synapse populations have so far resisted detailed quantitative study. In human brains and most animal nervous systems, synapses are very small and very densely packed: there are approximately 1 billion synapses per cubic millimeter of human cortex. This volumetric density poses very substantial challenges to proteometric analysis at the critical level of the individual synapse. The present work describes new probabilistic image analysis methods for single-synapse analysis of synapse populations in both animal and human brains.

Fast L1-NMF for Multiple Parametric Model Estimation

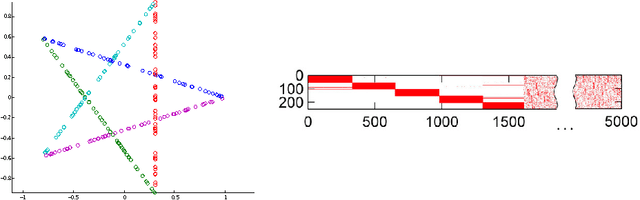
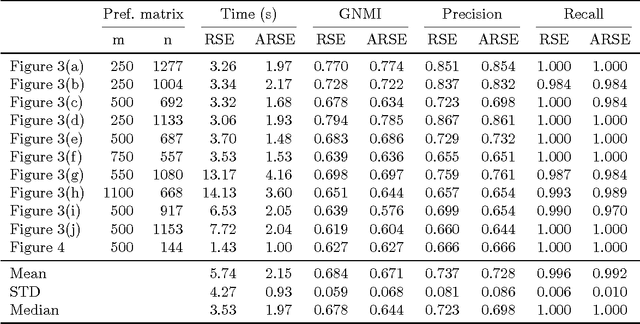
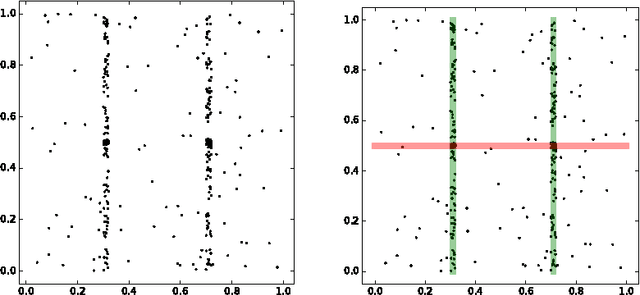
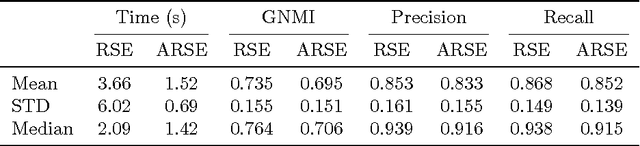
In this work we introduce a comprehensive algorithmic pipeline for multiple parametric model estimation. The proposed approach analyzes the information produced by a random sampling algorithm (e.g., RANSAC) from a machine learning/optimization perspective, using a \textit{parameterless} biclustering algorithm based on L1 nonnegative matrix factorization (L1-NMF). The proposed framework exploits consistent patterns that naturally arise during the RANSAC execution, while explicitly avoiding spurious inconsistencies. Contrarily to the main trends in the literature, the proposed technique does not impose non-intersecting parametric models. A new accelerated algorithm to compute L1-NMFs allows to handle medium-sized problems faster while also extending the usability of the algorithm to much larger datasets. This accelerated algorithm has applications in any other context where an L1-NMF is needed, beyond the biclustering approach to parameter estimation here addressed. We accompany the algorithmic presentation with theoretical foundations and numerous and diverse examples.

Dissimilarity-based Sparse Subset Selection

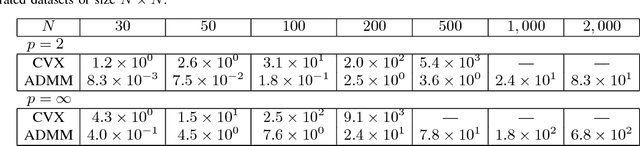
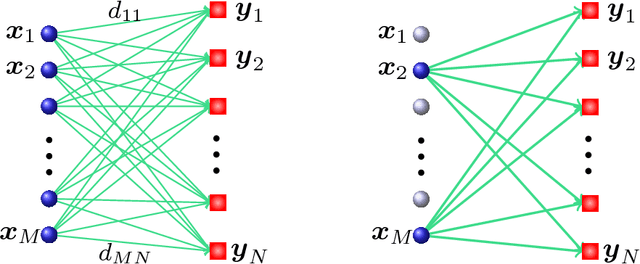
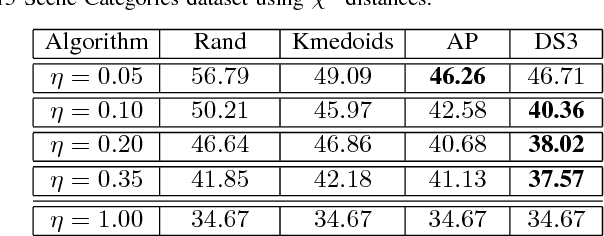
Finding an informative subset of a large collection of data points or models is at the center of many problems in computer vision, recommender systems, bio/health informatics as well as image and natural language processing. Given pairwise dissimilarities between the elements of a `source set' and a `target set,' we consider the problem of finding a subset of the source set, called representatives or exemplars, that can efficiently describe the target set. We formulate the problem as a row-sparsity regularized trace minimization problem. Since the proposed formulation is, in general, NP-hard, we consider a convex relaxation. The solution of our optimization finds representatives and the assignment of each element of the target set to each representative, hence, obtaining a clustering. We analyze the solution of our proposed optimization as a function of the regularization parameter. We show that when the two sets jointly partition into multiple groups, our algorithm finds representatives from all groups and reveals clustering of the sets. In addition, we show that the proposed framework can effectively deal with outliers. Our algorithm works with arbitrary dissimilarities, which can be asymmetric or violate the triangle inequality. To efficiently implement our algorithm, we consider an Alternating Direction Method of Multipliers (ADMM) framework, which results in quadratic complexity in the problem size. We show that the ADMM implementation allows to parallelize the algorithm, hence further reducing the computational time. Finally, by experiments on real-world datasets, we show that our proposed algorithm improves the state of the art on the two problems of scene categorization using representative images and time-series modeling and segmentation using representative~models.

Deep Neural Networks with Random Gaussian Weights: A Universal Classification Strategy?

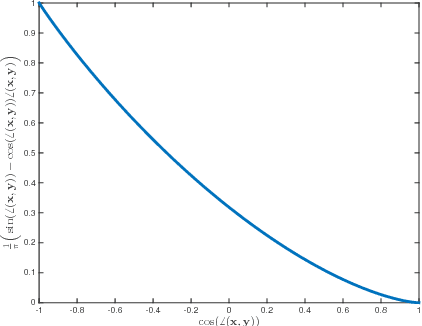
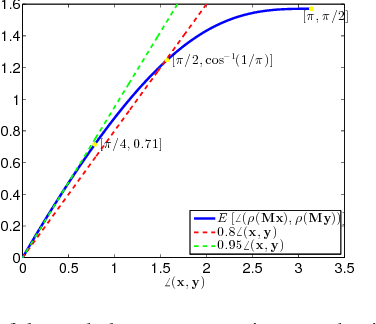
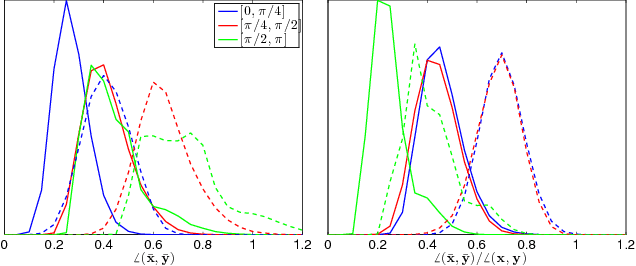
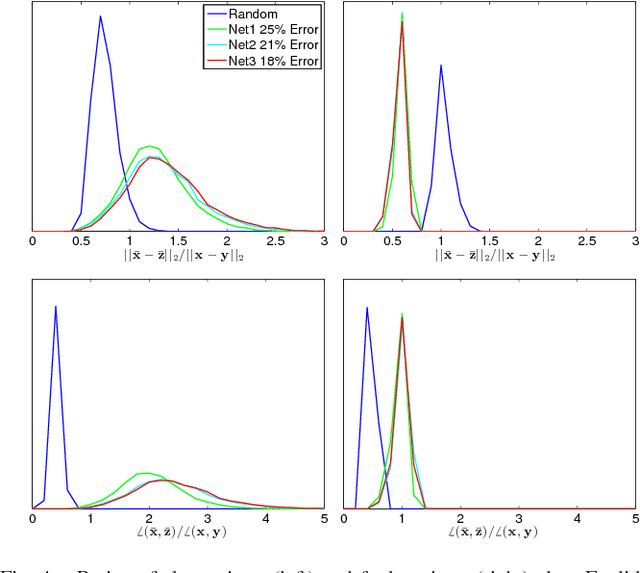
Three important properties of a classification machinery are: (i) the system preserves the core information of the input data; (ii) the training examples convey information about unseen data; and (iii) the system is able to treat differently points from different classes. In this work we show that these fundamental properties are satisfied by the architecture of deep neural networks. We formally prove that these networks with random Gaussian weights perform a distance-preserving embedding of the data, with a special treatment for in-class and out-of-class data. Similar points at the input of the network are likely to have a similar output. The theoretical analysis of deep networks here presented exploits tools used in the compressed sensing and dictionary learning literature, thereby making a formal connection between these important topics. The derived results allow drawing conclusions on the metric learning properties of the network and their relation to its structure, as well as providing bounds on the required size of the training set such that the training examples would represent faithfully the unseen data. The results are validated with state-of-the-art trained networks.

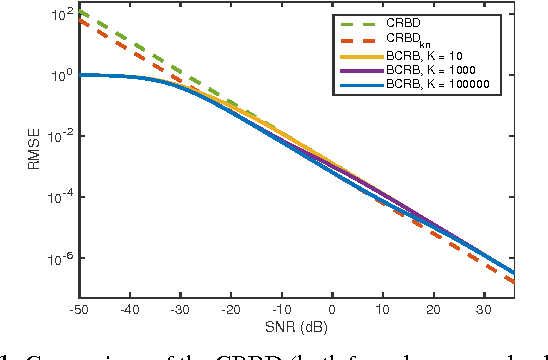
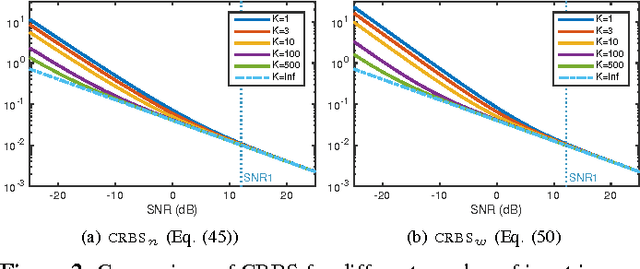
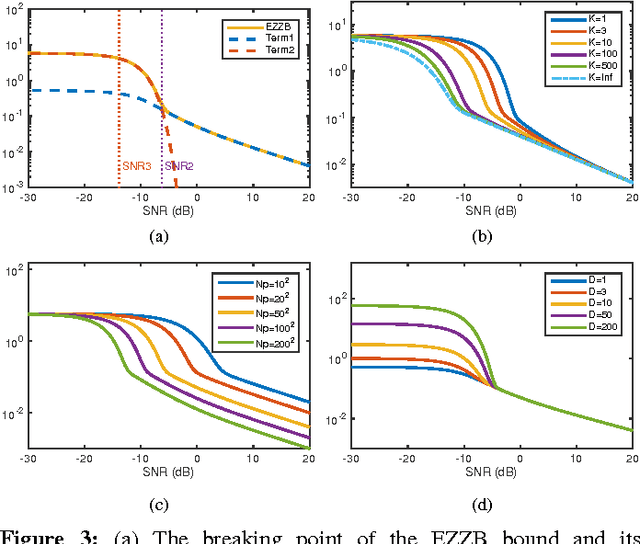
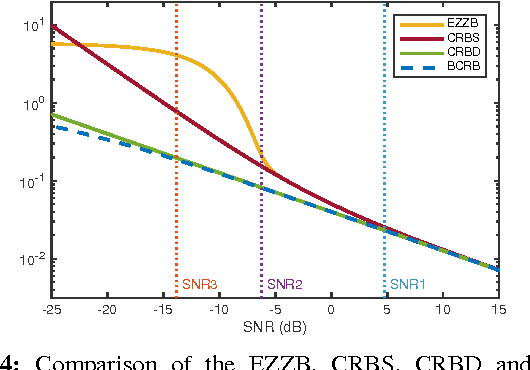
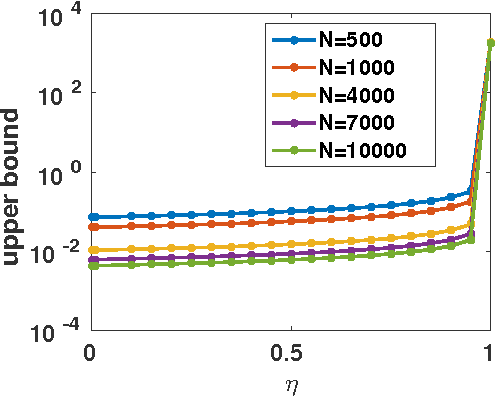
Fundamental Limits in Multi-image Alignment

The performance of multi-image alignment, bringing different images into one coordinate system, is critical in many applications with varied signal-to-noise ratio (SNR) conditions. A great amount of effort is being invested into developing methods to solve this problem. Several important questions thus arise, including: Which are the fundamental limits in multi-image alignment performance? Does having access to more images improve the alignment? Theoretical bounds provide a fundamental benchmark to compare methods and can help establish whether improvements can be made. In this work, we tackle the problem of finding the performance limits in image registration when multiple shifted and noisy observations are available. We derive and analyze the Cram\'er-Rao and Ziv-Zakai lower bounds under different statistical models for the underlying image. The accuracy of the derived bounds is experimentally assessed through a comparison to the maximum likelihood estimator. We show the existence of different behavior zones depending on the difficulty level of the problem, given by the SNR conditions of the input images. We find that increasing the number of images is only useful below a certain SNR threshold, above which the pairwise MLE estimation proves to be optimal. The analysis we present here brings further insight into the fundamental limitations of the multi-image alignment problem.

GraphConnect: A Regularization Framework for Neural Networks

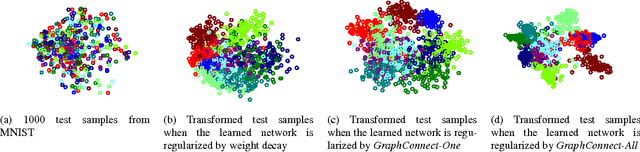
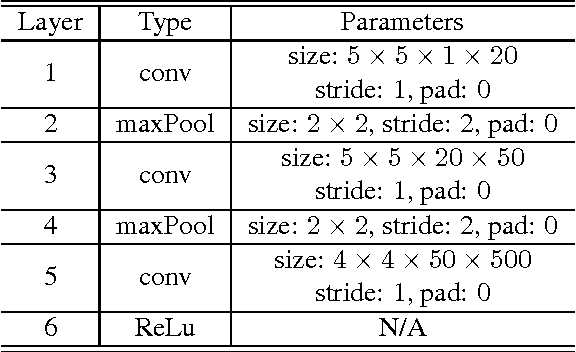
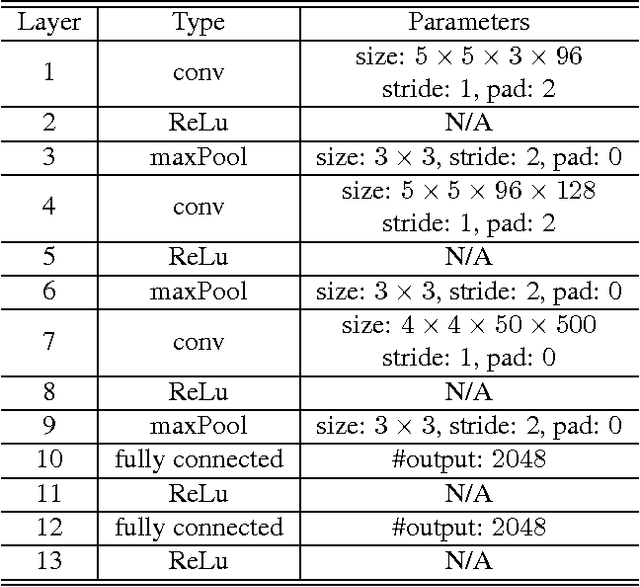
Deep neural networks have proved very successful in domains where large training sets are available, but when the number of training samples is small, their performance suffers from overfitting. Prior methods of reducing overfitting such as weight decay, Dropout and DropConnect are data-independent. This paper proposes a new method, GraphConnect, that is data-dependent, and is motivated by the observation that data of interest lie close to a manifold. The new method encourages the relationships between the learned decisions to resemble a graph representing the manifold structure. Essentially GraphConnect is designed to learn attributes that are present in data samples in contrast to weight decay, Dropout and DropConnect which are simply designed to make it more difficult to fit to random error or noise. Empirical Rademacher complexity is used to connect the generalization error of the neural network to spectral properties of the graph learned from the input data. This framework is used to show that GraphConnect is superior to weight decay. Experimental results on several benchmark datasets validate the theoretical analysis, and show that when the number of training samples is small, GraphConnect is able to significantly improve performance over weight decay.

Hand-held Video Deblurring via Efficient Fourier Aggregation

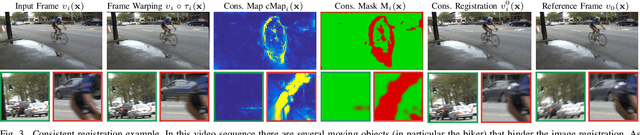
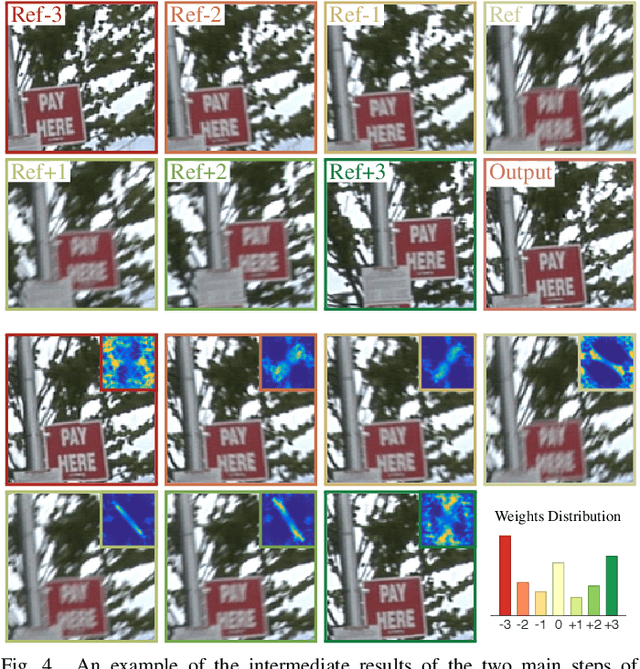
Videos captured with hand-held cameras often suffer from a significant amount of blur, mainly caused by the inevitable natural tremor of the photographer's hand. In this work, we present an algorithm that removes blur due to camera shake by combining information in the Fourier domain from nearby frames in a video. The dynamic nature of typical videos with the presence of multiple moving objects and occlusions makes this problem of camera shake removal extremely challenging, in particular when low complexity is needed. Given an input video frame, we first create a consistent registered version of temporally adjacent frames. Then, the set of consistently registered frames is block-wise fused in the Fourier domain with weights depending on the Fourier spectrum magnitude. The method is motivated from the physiological fact that camera shake blur has a random nature and therefore, nearby video frames are generally blurred differently. Experiments with numerous videos recorded in the wild, along with extensive comparisons, show that the proposed algorithm achieves state-of-the-art results while at the same time being much faster than its competitors.

Removing Camera Shake via Weighted Fourier Burst Accumulation

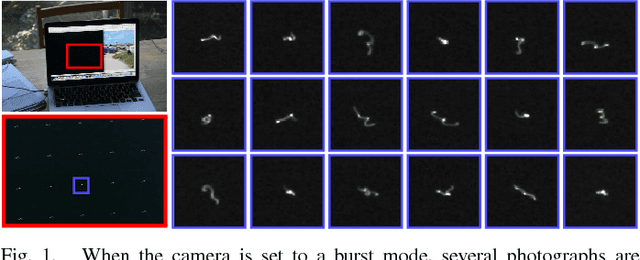
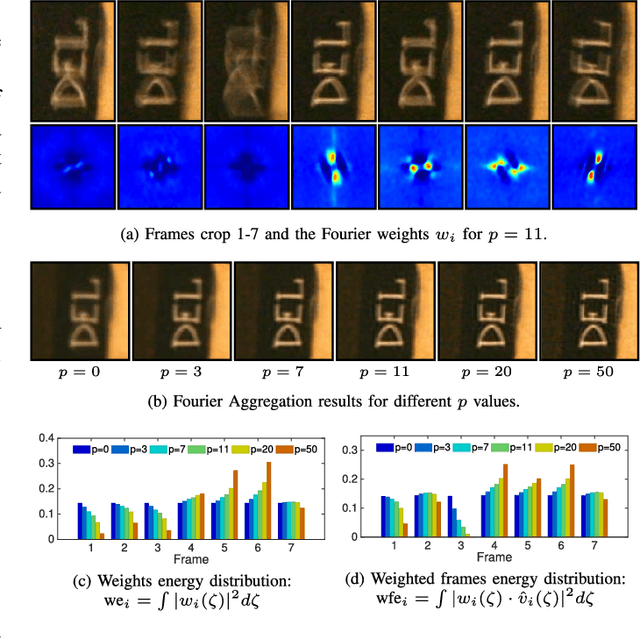
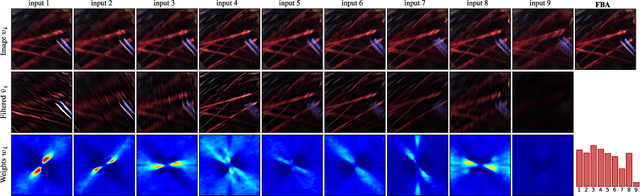
Numerous recent approaches attempt to remove image blur due to camera shake, either with one or multiple input images, by explicitly solving an inverse and inherently ill-posed deconvolution problem. If the photographer takes a burst of images, a modality available in virtually all modern digital cameras, we show that it is possible to combine them to get a clean sharp version. This is done without explicitly solving any blur estimation and subsequent inverse problem. The proposed algorithm is strikingly simple: it performs a weighted average in the Fourier domain, with weights depending on the Fourier spectrum magnitude. The method can be seen as a generalization of the align and average procedure, with a weighted average, motivated by hand-shake physiology and theoretically supported, taking place in the Fourier domain. The method's rationale is that camera shake has a random nature and therefore each image in the burst is generally blurred differently. Experiments with real camera data, and extensive comparisons, show that the proposed Fourier Burst Accumulation (FBA) algorithm achieves state-of-the-art results an order of magnitude faster, with simplicity for on-board implementation on camera phones. Finally, we also present experiments in real high dynamic range (HDR) scenes, showing how the method can be straightforwardly extended to HDR photography.