Scale-Equivariant Neural Networks with Decomposed Convolutional Filters

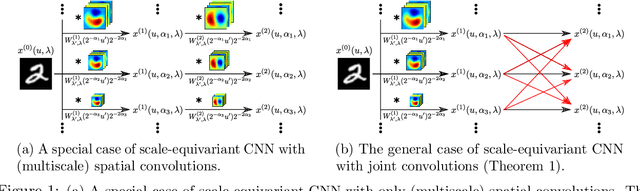
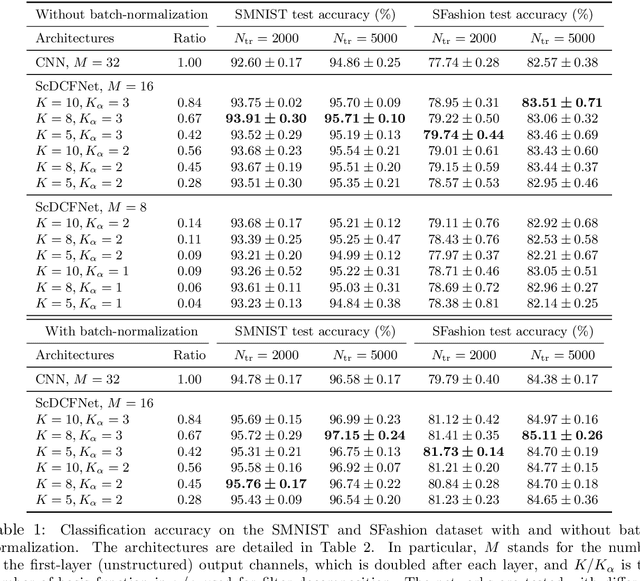
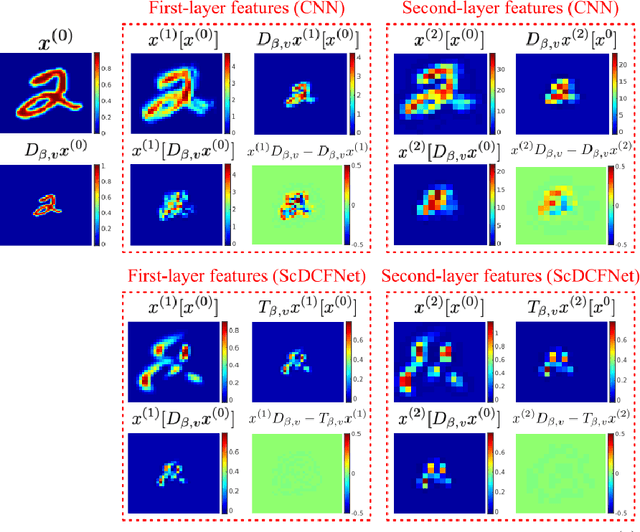
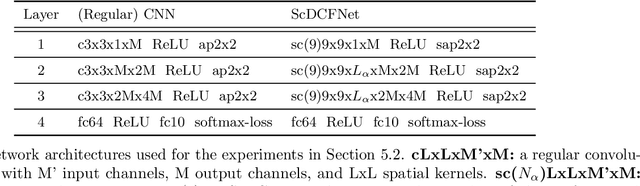
Encoding the input scale information explicitly into the representation learned by a convolutional neural network (CNN) is beneficial for many vision tasks especially when dealing with multiscale input signals. We study, in this paper, a scale-equivariant CNN architecture with joint convolutions across the space and the scaling group, which is shown to be both sufficient and necessary to achieve scale-equivariant representations. To reduce the model complexity and computational burden, we decompose the convolutional filters under two pre-fixed separable bases and truncate the expansion to low-frequency components. A further benefit of the truncated filter expansion is the improved deformation robustness of the equivariant representation. Numerical experiments demonstrate that the proposed scale-equivariant neural network with decomposed convolutional filters (ScDCFNet) achieves significantly improved performance in multiscale image classification and better interpretability than regular CNNs at a reduced model size.

Detecting Adversarial Samples Using Influence Functions and Nearest Neighbors

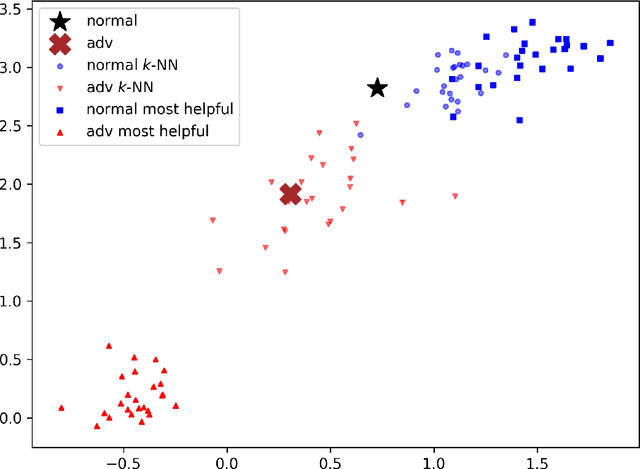
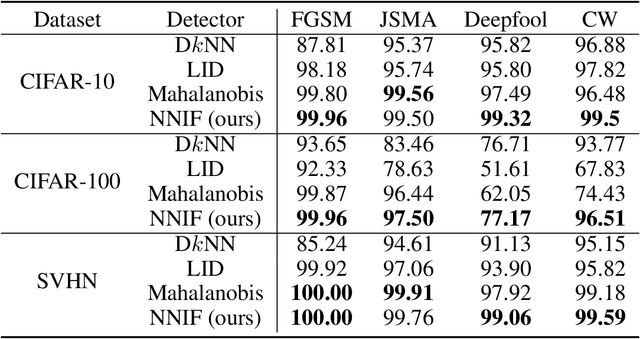
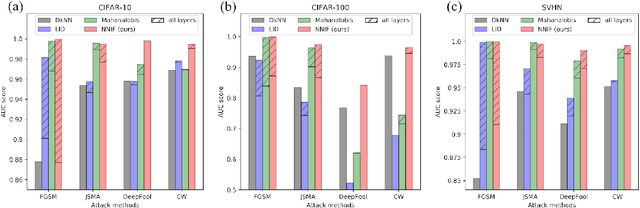
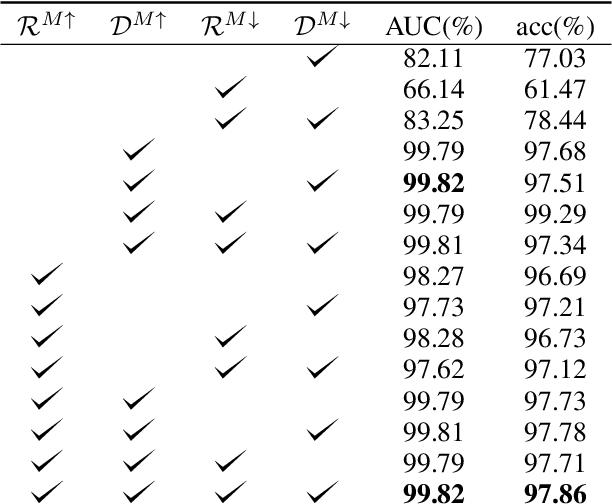
Deep neural networks (DNNs) are notorious for their vulnerability to adversarial attacks, which are small perturbations added to their input images to mislead their prediction. Detection of adversarial examples is, therefore, a fundamental requirement for robust classification frameworks. In this work, we present a method for detecting such adversarial attacks, which is suitable for any pre-trained neural network classifier. We use influence functions to measure the impact of every training sample on the validation set data. From the influence scores, we find the most supportive training samples for any given validation example. A k-nearest neighbor (k-NN) model fitted on the DNN's activation layers is employed to search for the ranking of these supporting training samples. We observe that these samples are highly correlated with the nearest neighbors of the normal inputs, while this correlation is much weaker for adversarial inputs. We train an adversarial detector using the k-NN ranks and distances and show that it successfully distinguishes adversarial examples, getting state-of-the-art results on four attack methods with three datasets.

Continuous Dice Coefficient: a Method for Evaluating Probabilistic Segmentations

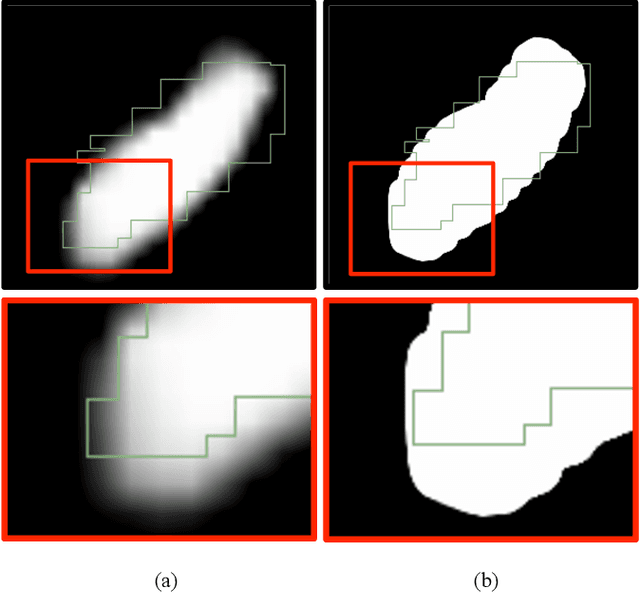
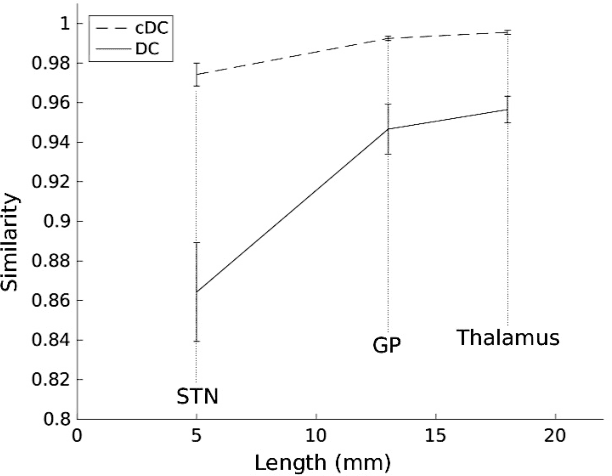
Objective: Overlapping measures are often utilized to quantify the similarity between two binary regions. However, modern segmentation algorithms output a probability or confidence map with continuous values in the zero-to-one interval. Moreover, these binary overlapping measures are biased to structure size. Addressing these challenges is the objective of this work. Methods: We extend the definition of the classical Dice coefficient (DC) overlap to facilitate the direct comparison of a ground truth binary image with a probabilistic map. We call the extended method continuous Dice coefficient (cDC) and show that 1) cDC is less or equal to 1 and cDC = 1 if-and-only-if the structures overlap is complete, and, 2) cDC is monotonically decreasing with the amount of overlap. We compare the classical DC and the cDC in a simulation of partial volume effects that incorporates segmentations of common targets for deep-brainstimulation. Lastly, we investigate the cDC for an automatic segmentation of the subthalamic-nucleus. Results: Partial volume effect simulation on thalamus (large structure) resulted with DC and cDC averages (SD) of 0.98 (0.006) and 0.99 (0.001), respectively. For subthalamic-nucleus (small structure) DC and cDC were 0.86 (0.025) and 0.97 (0.006), respectively. The DC and cDC for automatic STN segmentation were 0.66 and 0.80, respectively. Conclusion: The cDC is well defined for probabilistic segmentation, less biased to structure size and more robust to partial volume effects in comparison to DC. Significance: The proposed method facilitates a better evaluation of segmentation algorithms. As a better measurement tool, it opens the door for the development of better segmentation methods.

Non-contact photoplethysmogram and instantaneous heart rate estimation from infrared face video

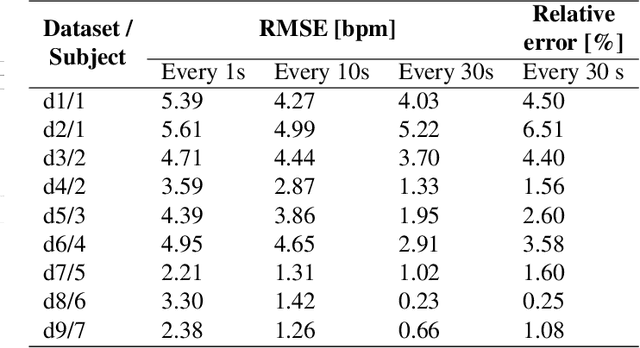
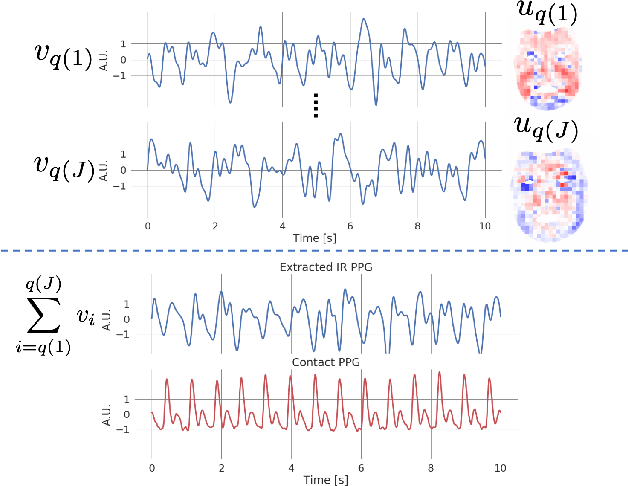
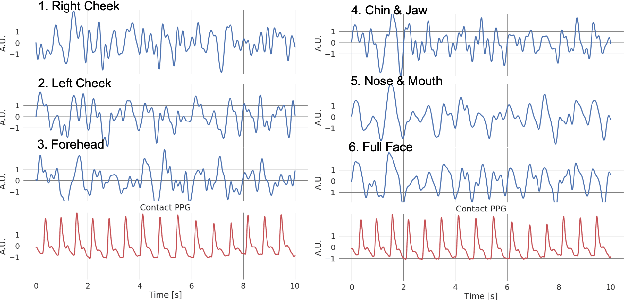
Extracting the instantaneous heart rate (iHR) from face videos has been well studied in recent years. It is well known that changes in skin color due to blood flow can be captured using conventional cameras. One of the main limitations of methods that rely on this principle is the need of an illumination source. Moreover, they have to be able to operate under different light conditions. One way to avoid these constraints is using infrared cameras, allowing the monitoring of iHR under low light conditions. In this work, we present a simple, principled signal extraction method that recovers the iHR from infrared face videos. We tested the procedure on 7 participants, for whom we recorded an electrocardiogram simultaneously with their infrared face video. We checked that the recovered signal matched the ground truth iHR, showing that infrared is a promising alternative to conventional video imaging for heart rate monitoring, especially in low light conditions. Code is available at https://github.com/natalialmg/IR_iHR

Stop memorizing: A data-dependent regularization framework for intrinsic pattern learning

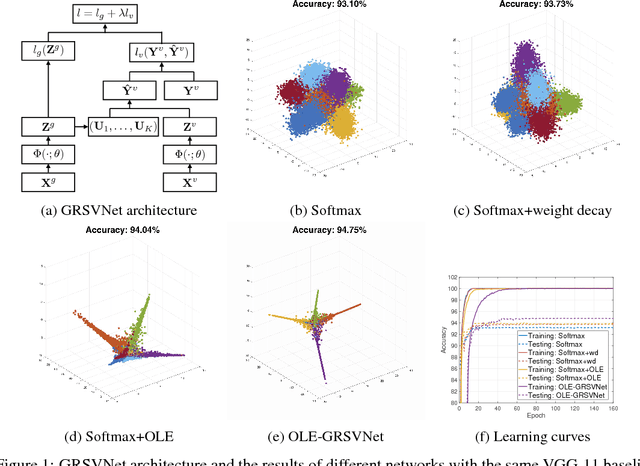
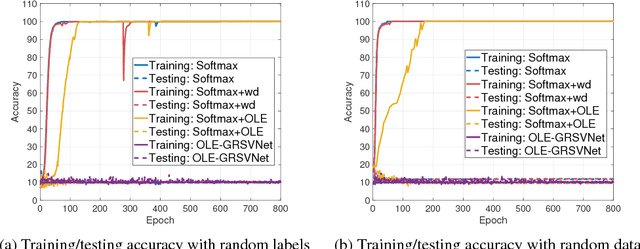
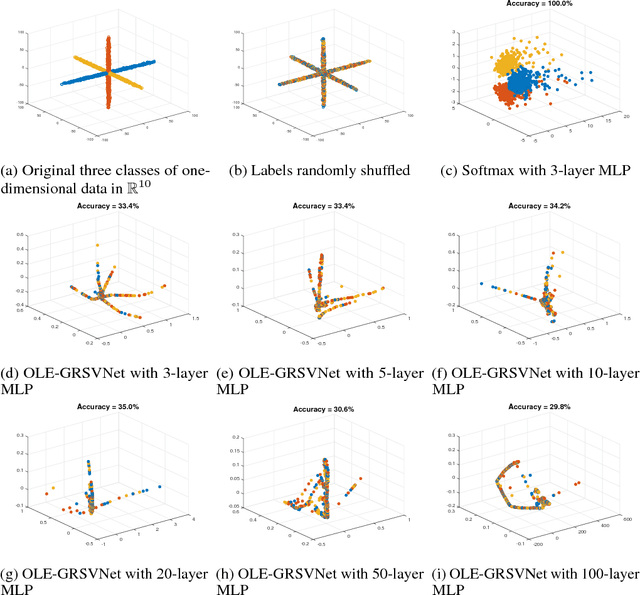
Deep neural networks (DNNs) typically have enough capacity to fit random data by brute force even when conventional data-dependent regularizations focusing on the geometry of the features are imposed. We find out that the reason for this is the inconsistency between the enforced geometry and the standard softmax cross entropy loss. To resolve this, we propose a new framework for data-dependent DNN regularization, the Geometrically-Regularized-Self-Validating neural Networks (GRSVNet). During training, the geometry enforced on one batch of features is simultaneously validated on a separate batch using a validation loss consistent with the geometry. We study a particular case of GRSVNet, the Orthogonal-Low-rank Embedding (OLE)-GRSVNet, which is capable of producing highly discriminative features residing in orthogonal low-rank subspaces. Numerical experiments show that OLE-GRSVNet outperforms DNNs with conventional regularization when trained on real data. More importantly, unlike conventional DNNs, OLE-GRSVNet refuses to memorize random data or random labels, suggesting it only learns intrinsic patterns by reducing the memorizing capacity of the baseline DNN.

ForestHash: Semantic Hashing With Shallow Random Forests and Tiny Convolutional Networks

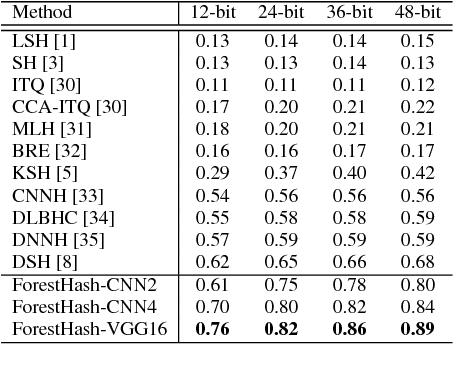
Hash codes are efficient data representations for coping with the ever growing amounts of data. In this paper, we introduce a random forest semantic hashing scheme that embeds tiny convolutional neural networks (CNN) into shallow random forests, with near-optimal information-theoretic code aggregation among trees. We start with a simple hashing scheme, where random trees in a forest act as hashing functions by setting `1' for the visited tree leaf, and `0' for the rest. We show that traditional random forests fail to generate hashes that preserve the underlying similarity between the trees, rendering the random forests approach to hashing challenging. To address this, we propose to first randomly group arriving classes at each tree split node into two groups, obtaining a significantly simplified two-class classification problem, which can be handled using a light-weight CNN weak learner. Such random class grouping scheme enables code uniqueness by enforcing each class to share its code with different classes in different trees. A non-conventional low-rank loss is further adopted for the CNN weak learners to encourage code consistency by minimizing intra-class variations and maximizing inter-class distance for the two random class groups. Finally, we introduce an information-theoretic approach for aggregating codes of individual trees into a single hash code, producing a near-optimal unique hash for each class. The proposed approach significantly outperforms state-of-the-art hashing methods for image retrieval tasks on large-scale public datasets, while performing at the level of other state-of-the-art image classification techniques while utilizing a more compact and efficient scalable representation. This work proposes a principled and robust procedure to train and deploy in parallel an ensemble of light-weight CNNs, instead of simply going deeper.

DCFNet: Deep Neural Network with Decomposed Convolutional Filters

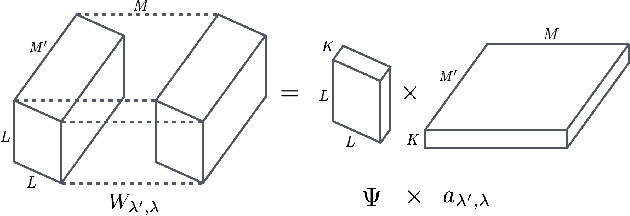
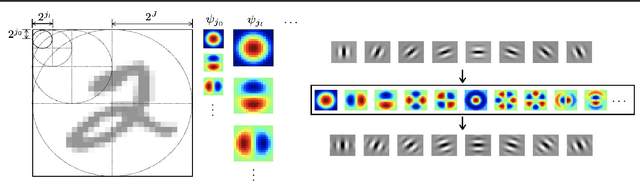
Filters in a Convolutional Neural Network (CNN) contain model parameters learned from enormous amounts of data. In this paper, we suggest to decompose convolutional filters in CNN as a truncated expansion with pre-fixed bases, namely the Decomposed Convolutional Filters network (DCFNet), where the expansion coefficients remain learned from data. Such a structure not only reduces the number of trainable parameters and computation, but also imposes filter regularity by bases truncation. Through extensive experiments, we consistently observe that DCFNet maintains accuracy for image classification tasks with a significant reduction of model parameters, particularly with Fourier-Bessel (FB) bases, and even with random bases. Theoretically, we analyze the representation stability of DCFNet with respect to input variations, and prove representation stability under generic assumptions on the expansion coefficients. The analysis is consistent with the empirical observations.

DNN or $k$-NN: That is the Generalize vs. Memorize Question

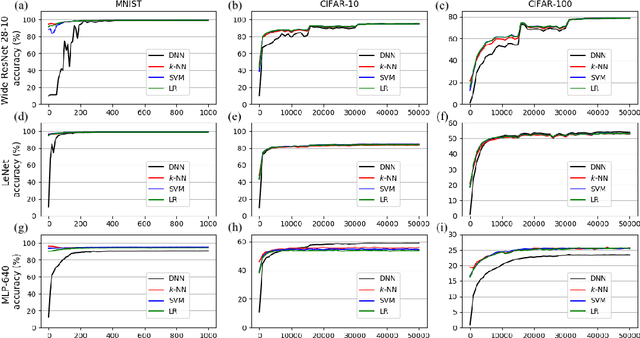
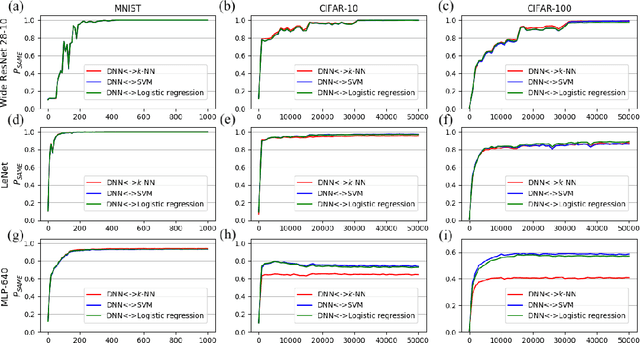
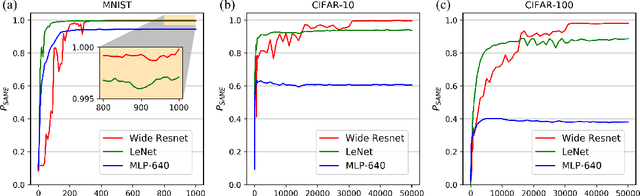
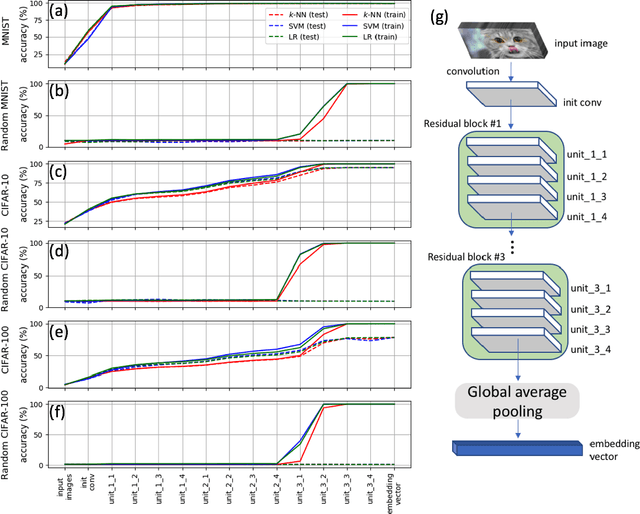
This paper studies the relationship between the classification performed by deep neural networks and the $k$-NN decision at the embedding space of these networks. This simple important connection shown here provides a better understanding of the relationship between the ability of neural networks to generalize and their tendency to memorize the training data, which are traditionally considered to be contradicting to each other and here shown to be compatible and complementary. Our results support the conjecture that deep neural networks approach Bayes optimal error rates.

Learning to Collaborate for User-Controlled Privacy

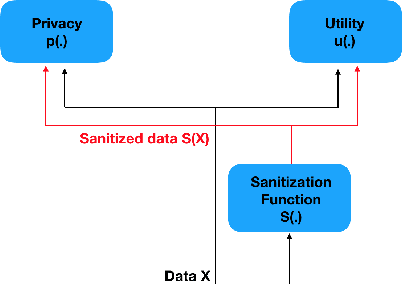
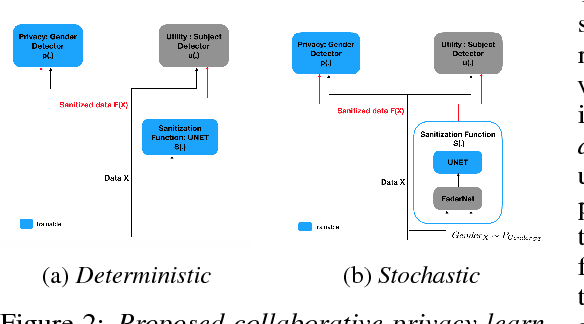
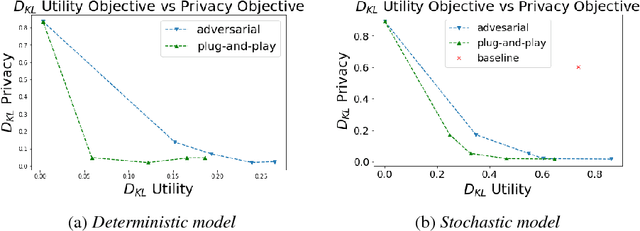
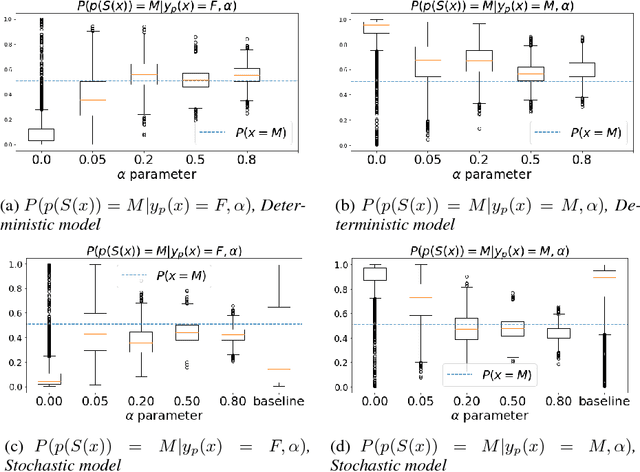
It is becoming increasingly clear that users should own and control their data. Utility providers are also becoming more interested in guaranteeing data privacy. As such, users and utility providers should collaborate in data privacy, a paradigm that has not yet been developed in the privacy research community. We introduce this concept and present explicit architectures where the user controls what characteristics of the data she/he wants to share and what she/he wants to keep private. This is achieved by collaborative learning a sensitization function, either a deterministic or a stochastic one, that retains valuable information for the utility tasks but it also eliminates necessary information for the privacy ones. As illustration examples, we implement them using a plug-and-play approach, where no algorithm is changed at the system provider end, and an adversarial approach, where minor re-training of the privacy inferring engine is allowed. In both cases the learned sanitization function keeps the data in the original domain, thereby allowing the system to use the same algorithms it was using before for both original and privatized data. We show how we can maintain utility while fully protecting private information if the user chooses to do so, even when the first is harder than the second, as in the case here illustrated of identity detection while hiding gender.

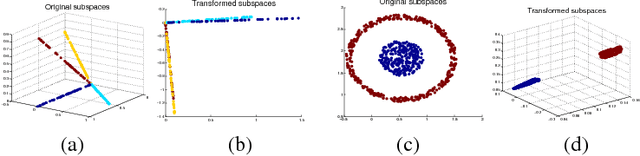
RotDCF: Decomposition of Convolutional Filters for Rotation-Equivariant Deep Networks

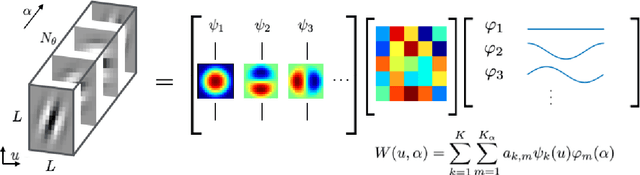
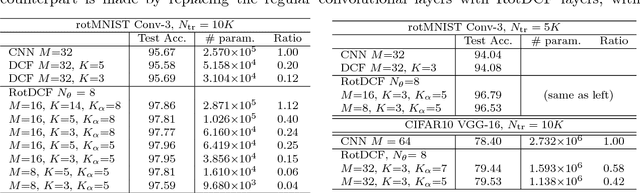
Explicit encoding of group actions in deep features makes it possible for convolutional neural networks (CNNs) to handle global deformations of images, which is critical to success in many vision tasks. This paper proposes to decompose the convolutional filters over joint steerable bases across the space and the group geometry simultaneously, namely a rotation-equivariant CNN with decomposed convolutional filters (RotDCF). This decomposition facilitates computing the joint convolution, which is proved to be necessary for the group equivariance. It significantly reduces the model size and computational complexity while preserving performance, and truncation of the bases expansion serves implicitly to regularize the filters. On datasets involving in-plane and out-of-plane object rotations, RotDCF deep features demonstrate greater robustness and interpretability than regular CNNs. The stability of the equivariant representation to input variations is also proved theoretically under generic assumptions on the filters in the decomposed form. The RotDCF framework can be extended to groups other than rotations, providing a general approach which achieves both group equivariance and representation stability at a reduced model size.