Geometric implicit neural representations for signed distance functions

\textit{Implicit neural representations} (INRs) have emerged as a promising framework for representing signals in low-dimensional spaces. This survey reviews the existing literature on the specialized INR problem of approximating \textit{signed distance functions} (SDFs) for surface scenes, using either oriented point clouds or a set of posed images. We refer to neural SDFs that incorporate differential geometry tools, such as normals and curvatures, in their loss functions as \textit{geometric} INRs. The key idea behind this 3D reconstruction approach is to include additional \textit{regularization} terms in the loss function, ensuring that the INR satisfies certain global properties that the function should hold -- such as having unit gradient in the case of SDFs. We explore key methodological components, including the definition of INR, the construction of geometric loss functions, and sampling schemes from a differential geometry perspective. Our review highlights the significant advancements enabled by geometric INRs in surface reconstruction from oriented point clouds and posed images.

FLOWING: Implicit Neural Flows for Structure-Preserving Morphing

Morphing is a long-standing problem in vision and computer graphics, requiring a time-dependent warping for feature alignment and a blending for smooth interpolation. Recently, multilayer perceptrons (MLPs) have been explored as implicit neural representations (INRs) for modeling such deformations, due to their meshlessness and differentiability; however, extracting coherent and accurate morphings from standard MLPs typically relies on costly regularizations, which often lead to unstable training and prevent effective feature alignment. To overcome these limitations, we propose FLOWING (FLOW morphING), a framework that recasts warping as the construction of a differential vector flow, naturally ensuring continuity, invertibility, and temporal coherence by encoding structural flow properties directly into the network architectures. This flow-centric approach yields principled and stable transformations, enabling accurate and structure-preserving morphing of both 2D images and 3D shapes. Extensive experiments across a range of applications - including face and image morphing, as well as Gaussian Splatting morphing - show that FLOWING achieves state-of-the-art morphing quality with faster convergence. Code and pretrained models are available at http://schardong.github.io/flowing.

High-Resolution Detection of Earth Structural Heterogeneities from Seismic Amplitudes using Convolutional Neural Networks with Attention layers

Earth structural heterogeneities have a remarkable role in the petroleum economy for both exploration and production projects. Automatic detection of detailed structural heterogeneities is challenging when considering modern machine learning techniques like deep neural networks. Typically, these techniques can be an excellent tool for assisted interpretation of such heterogeneities, but it heavily depends on the amount of data to be trained. We propose an efficient and cost-effective architecture for detecting seismic structural heterogeneities using Convolutional Neural Networks (CNNs) combined with Attention layers. The attention mechanism reduces costs and enhances accuracy, even in cases with relatively noisy data. Our model has half the parameters compared to the state-of-the-art, and it outperforms previous methods in terms of Intersection over Union (IoU) by 0.6% and precision by 0.4%. By leveraging synthetic data, we apply transfer learning to train and fine-tune the model, addressing the challenge of limited annotated data availability.

Neural Implicit Morphing of Face Images

Face morphing is one of the seminal problems in computer graphics, with numerous artistic and forensic applications. It is notoriously challenging due to pose, lighting, gender, and ethnicity variations. Generally, this task consists of a warping for feature alignment and a blending for a seamless transition between the warped images. We propose to leverage coordinate-based neural networks to represent such warpings and blendings of face images. During training, we exploit the smoothness and flexibility of such networks, by combining energy functionals employed in classical approaches without discretizations. Additionally, our method is time-dependent, allowing a continuous warping, and blending of the target images. During warping inference, we need both direct and inverse transformations of the time-dependent warping. The first is responsible for morphing the target image into the source image, while the inverse is used for morphing in the opposite direction. Our neural warping stores those maps in a single network due to its inversible property, dismissing the hard task of inverting them. The results of our experiments indicate that our method is competitive with both classical and data-based neural techniques under the lens of face-morphing detection approaches. Aesthetically, the resulting images present a seamless blending of diverse faces not yet usual in the literature.

Multiresolution Neural Networks for Imaging

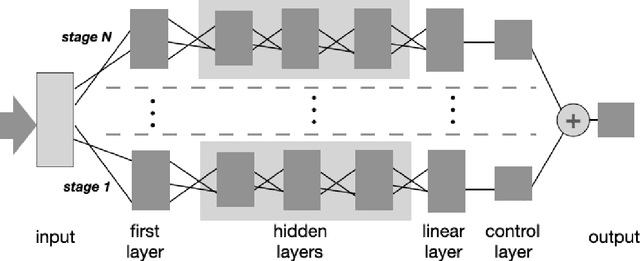
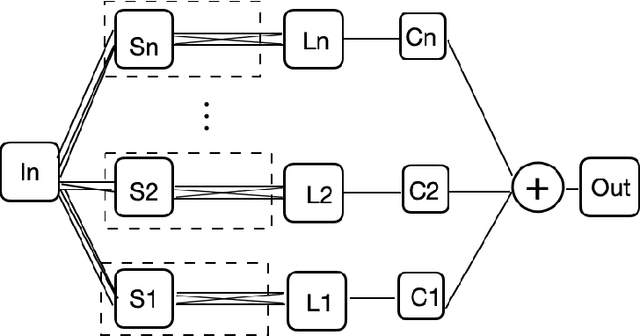
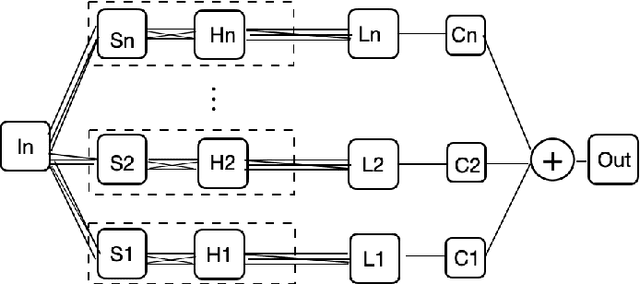
We present MR-Net, a general architecture for multiresolution neural networks, and a framework for imaging applications based on this architecture. Our coordinate-based networks are continuous both in space and in scale as they are composed of multiple stages that progressively add finer details. Besides that, they are a compact and efficient representation. We show examples of multiresolution image representation and applications to texturemagnification, minification, and antialiasing. This document is the extended version of the paper [PNS+22]. It includes additional material that would not fit the page limitations of the conference track for publication.

Neural Implicit Surfaces in Higher Dimension

This work investigates the use of neural networks admitting high-order derivatives for modeling dynamic variations of smooth implicit surfaces. For this purpose, it extends the representation of differentiable neural implicit surfaces to higher dimensions, which opens up mechanisms that allow to exploit geometric transformations in many settings, from animation and surface evolution to shape morphing and design galleries. The problem is modeled by a $k$-parameter family of surfaces $S_c$, specified as a neural network function $f : \mathbb{R}^3 \times \mathbb{R}^k \rightarrow \mathbb{R}$, where $S_c$ is the zero-level set of the implicit function $f(\cdot, c) : \mathbb{R}^3 \rightarrow \mathbb{R} $, with $c \in \mathbb{R}^k$, with variations induced by the control variable $c$. In that context, restricted to each coordinate of $\mathbb{R}^k$, the underlying representation is a neural homotopy which is the solution of a general partial differential equation.

Differential Geometry in Neural Implicits

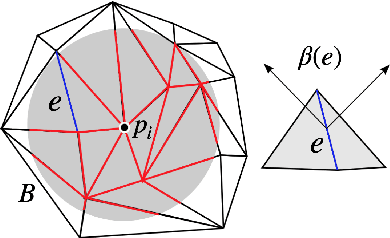
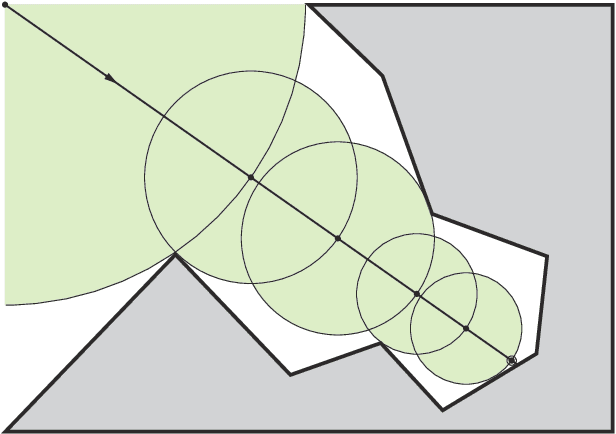
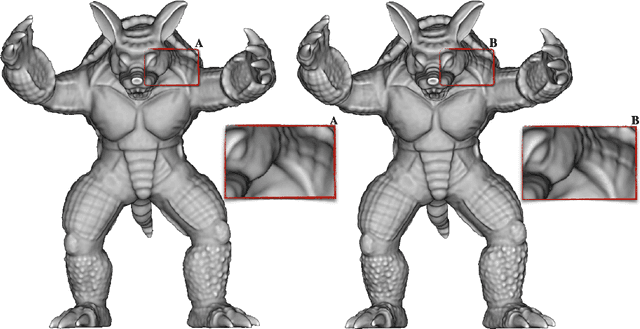
We introduce a neural implicit framework that bridges discrete differential geometry of triangle meshes and continuous differential geometry of neural implicit surfaces. It exploits the differentiable properties of neural networks and the discrete geometry of triangle meshes to approximate them as the zero-level sets of neural implicit functions. To train a neural implicit function, we propose a loss function that allows terms with high-order derivatives, such as the alignment between the principal directions, to learn more geometric details. During training, we consider a non-uniform sampling strategy based on the discrete curvatures of the triangle mesh to access points with more geometric details. This sampling implies faster learning while preserving geometric accuracy. We present the analytical differential geometry formulas for neural surfaces, such as normal vectors and curvatures. We use them to render the surfaces using sphere tracing. Additionally, we propose a network optimization based on singular value decomposition to reduce the number of parameters.