SASNet: Spatially-Adaptive Sinusoidal Neural Networks

Sinusoidal neural networks (SNNs) have emerged as powerful implicit neural representations (INRs) for low-dimensional signals in computer vision and graphics. They enable high-frequency signal reconstruction and smooth manifold modeling; however, they often suffer from spectral bias, training instability, and overfitting. To address these challenges, we propose SASNet, Spatially-Adaptive SNNs that robustly enhance the capacity of compact INRs to fit detailed signals. SASNet integrates a frequency embedding layer to control frequency components and mitigate spectral bias, along with jointly optimized, spatially-adaptive masks that localize neuron influence, reducing network redundancy and improving convergence stability. Robust to hyperparameter selection, SASNet faithfully reconstructs high-frequency signals without overfitting low-frequency regions. Our experiments show that SASNet outperforms state-of-the-art INRs, achieving strong fitting accuracy, super-resolution capability, and noise suppression, without sacrificing model compactness.

Neural 4D Evolution under Large Topological Changes from 2D Images

In the literature, it has been shown that the evolution of the known explicit 3D surface to the target one can be learned from 2D images using the instantaneous flow field, where the known and target 3D surfaces may largely differ in topology. We are interested in capturing 4D shapes whose topology changes largely over time. We encounter that the straightforward extension of the existing 3D-based method to the desired 4D case performs poorly. In this work, we address the challenges in extending 3D neural evolution to 4D under large topological changes by proposing two novel modifications. More precisely, we introduce (i) a new architecture to discretize and encode the deformation and learn the SDF and (ii) a technique to impose the temporal consistency. (iii) Also, we propose a rendering scheme for color prediction based on Gaussian splatting. Furthermore, to facilitate learning directly from 2D images, we propose a learning framework that can disentangle the geometry and appearance from RGB images. This method of disentanglement, while also useful for the 4D evolution problem that we are concentrating on, is also novel and valid for static scenes. Our extensive experiments on various data provide awesome results and, most importantly, open a new approach toward reconstructing challenging scenes with significant topological changes and deformations. Our source code and the dataset are publicly available at https://github.com/insait-institute/N4DE.

Taming the Frequency Factory of Sinusoidal Networks

This work investigates the structure and representation capacity of $sinusoidal$ MLPs, which have recently shown promising results in encoding low-dimensional signals. This success can be attributed to its smoothness and high representation capacity. The first allows the use of the network's derivatives during training, enabling regularization. However, defining the architecture and initializing its parameters to achieve a desired capacity remains an empirical task. This work provides theoretical and experimental results justifying the capacity property of sinusoidal MLPs and offers control mechanisms for their initialization and training. We approach this from a Fourier series perspective and link the training with the model's spectrum. Our analysis is based on a $harmonic$ expansion of the sinusoidal MLP, which says that the composition of sinusoidal layers produces a large number of new frequencies expressed as integer linear combinations of the input frequencies (weights of the input layer). We use this novel $identity$ to initialize the input neurons which work as a sampling in the signal spectrum. We also note that each hidden neuron produces the same frequencies with amplitudes completely determined by the hidden weights. Finally, we give an upper bound for these amplitudes, which results in a $bounding$ scheme for the network's spectrum during training.

Implicit Neural Representation of Tileable Material Textures

We explore sinusoidal neural networks to represent periodic tileable textures. Our approach leverages the Fourier series by initializing the first layer of a sinusoidal neural network with integer frequencies with a period $P$. We prove that the compositions of sinusoidal layers generate only integer frequencies with period $P$. As a result, our network learns a continuous representation of a periodic pattern, enabling direct evaluation at any spatial coordinate without the need for interpolation. To enforce the resulting pattern to be tileable, we add a regularization term, based on the Poisson equation, to the loss function. Our proposed neural implicit representation is compact and enables efficient reconstruction of high-resolution textures with high visual fidelity and sharpness across multiple levels of detail. We present applications of our approach in the domain of anti-aliased surface.

Neural Implicit Morphing of Face Images

Face morphing is one of the seminal problems in computer graphics, with numerous artistic and forensic applications. It is notoriously challenging due to pose, lighting, gender, and ethnicity variations. Generally, this task consists of a warping for feature alignment and a blending for a seamless transition between the warped images. We propose to leverage coordinate-based neural networks to represent such warpings and blendings of face images. During training, we exploit the smoothness and flexibility of such networks, by combining energy functionals employed in classical approaches without discretizations. Additionally, our method is time-dependent, allowing a continuous warping, and blending of the target images. During warping inference, we need both direct and inverse transformations of the time-dependent warping. The first is responsible for morphing the target image into the source image, while the inverse is used for morphing in the opposite direction. Our neural warping stores those maps in a single network due to its inversible property, dismissing the hard task of inverting them. The results of our experiments indicate that our method is competitive with both classical and data-based neural techniques under the lens of face-morphing detection approaches. Aesthetically, the resulting images present a seamless blending of diverse faces not yet usual in the literature.

Understanding Sinusoidal Neural Networks

In this work, we investigate the representation capacity of multilayer perceptron networks that use the sine as activation function - sinusoidal neural networks. We show that the layer composition in such networks compacts information. For this, we prove that the composition of sinusoidal layers expands as a sum of sines consisting of a large number of new frequencies given by linear combinations of the weights of the network's first layer. We provide the expression of the corresponding amplitudes in terms of the Bessel functions and give an upper bound for them that can be used to control the resulting approximation.

Multiresolution Neural Networks for Imaging

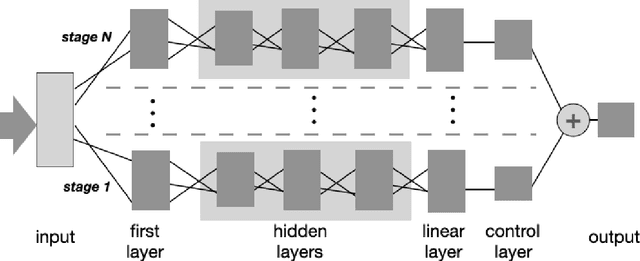
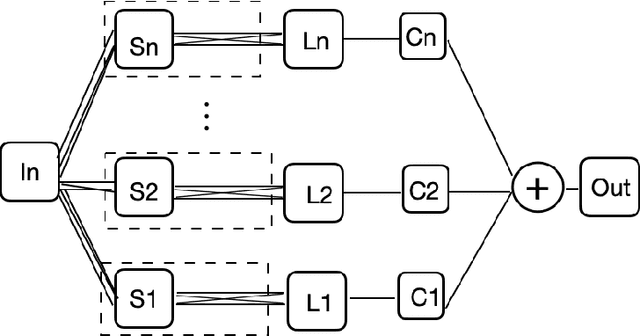
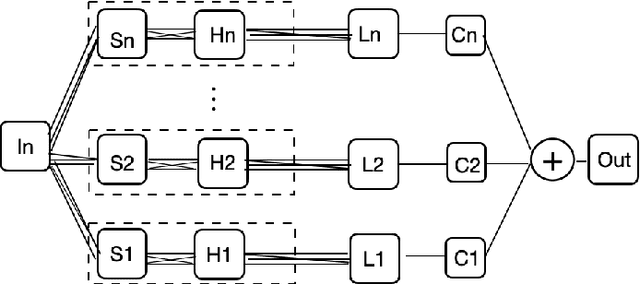
We present MR-Net, a general architecture for multiresolution neural networks, and a framework for imaging applications based on this architecture. Our coordinate-based networks are continuous both in space and in scale as they are composed of multiple stages that progressively add finer details. Besides that, they are a compact and efficient representation. We show examples of multiresolution image representation and applications to texturemagnification, minification, and antialiasing. This document is the extended version of the paper [PNS+22]. It includes additional material that would not fit the page limitations of the conference track for publication.

Neural Implicit Surfaces in Higher Dimension

This work investigates the use of neural networks admitting high-order derivatives for modeling dynamic variations of smooth implicit surfaces. For this purpose, it extends the representation of differentiable neural implicit surfaces to higher dimensions, which opens up mechanisms that allow to exploit geometric transformations in many settings, from animation and surface evolution to shape morphing and design galleries. The problem is modeled by a $k$-parameter family of surfaces $S_c$, specified as a neural network function $f : \mathbb{R}^3 \times \mathbb{R}^k \rightarrow \mathbb{R}$, where $S_c$ is the zero-level set of the implicit function $f(\cdot, c) : \mathbb{R}^3 \rightarrow \mathbb{R} $, with $c \in \mathbb{R}^k$, with variations induced by the control variable $c$. In that context, restricted to each coordinate of $\mathbb{R}^k$, the underlying representation is a neural homotopy which is the solution of a general partial differential equation.

Differential Geometry in Neural Implicits

We introduce a neural implicit framework that bridges discrete differential geometry of triangle meshes and continuous differential geometry of neural implicit surfaces. It exploits the differentiable properties of neural networks and the discrete geometry of triangle meshes to approximate them as the zero-level sets of neural implicit functions. To train a neural implicit function, we propose a loss function that allows terms with high-order derivatives, such as the alignment between the principal directions, to learn more geometric details. During training, we consider a non-uniform sampling strategy based on the discrete curvatures of the triangle mesh to access points with more geometric details. This sampling implies faster learning while preserving geometric accuracy. We present the analytical differential geometry formulas for neural surfaces, such as normal vectors and curvatures. We use them to render the surfaces using sphere tracing. Additionally, we propose a network optimization based on singular value decomposition to reduce the number of parameters.