Digital Computers Break the Curse of Dimensionality: Adaptive Bounds via Finite Geometry

Many of the foundations of machine learning rely on the idealized premise that all input and output spaces are infinite, e.g.~$\mathbb{R}^d$. This core assumption is systematically violated in practice due to digital computing limitations from finite machine precision, rounding, and limited RAM. In short, digital computers operate on finite grids in $\mathbb{R}^d$. By exploiting these discrete structures, we show the curse of dimensionality in statistical learning is systematically broken when models are implemented on real computers. Consequentially, we obtain new generalization bounds with dimension-free rates for kernel and deep ReLU MLP regressors, which are implemented on real-world machines. Our results are derived using a new non-asymptotic concentration of measure result between a probability measure over any finite metric space and its empirical version associated with $N$ i.i.d. samples when measured in the $1$-Wasserstein distance. Unlike standard concentration of measure results, the concentration rates in our bounds do not hold uniformly for all sample sizes $N$; instead, our rates can adapt to any given $N$. This yields significantly tighter bounds for realistic sample sizes while achieving the optimal worst-case rate of $\mathcal{O}(1/N^{1/2})$ for massive. Our results are built on new techniques combining metric embedding theory with optimal transport

Estimating Barycenters of Distributions with Neural Optimal Transport

Given a collection of probability measures, a practitioner sometimes needs to find an "average" distribution which adequately aggregates reference distributions. A theoretically appealing notion of such an average is the Wasserstein barycenter, which is the primal focus of our work. By building upon the dual formulation of Optimal Transport (OT), we propose a new scalable approach for solving the Wasserstein barycenter problem. Our methodology is based on the recent Neural OT solver: it has bi-level adversarial learning objective and works for general cost functions. These are key advantages of our method, since the typical adversarial algorithms leveraging barycenter tasks utilize tri-level optimization and focus mostly on quadratic cost. We also establish theoretical error bounds for our proposed approach and showcase its applicability and effectiveness on illustrative scenarios and image data setups.

Energy-Guided Continuous Entropic Barycenter Estimation for General Costs

Optimal transport (OT) barycenters are a mathematically grounded way of averaging probability distributions while capturing their geometric properties. In short, the barycenter task is to take the average of a collection of probability distributions w.r.t. given OT discrepancies. We propose a novel algorithm for approximating the continuous Entropic OT (EOT) barycenter for arbitrary OT cost functions. Our approach is built upon the dual reformulation of the EOT problem based on weak OT, which has recently gained the attention of the ML community. Beyond its novelty, our method enjoys several advantageous properties: (i) we establish quality bounds for the recovered solution; (ii) this approach seemlessly interconnects with the Energy-Based Models (EBMs) learning procedure enabling the use of well-tuned algorithms for the problem of interest; (iii) it provides an intuitive optimization scheme avoiding min-max, reinforce and other intricate technical tricks. For validation, we consider several low-dimensional scenarios and image-space setups, including non-Euclidean cost functions. Furthermore, we investigate the practical task of learning the barycenter on an image manifold generated by a pretrained generative model, opening up new directions for real-world applications.

Metric Hypertransformers are Universal Adapted Maps

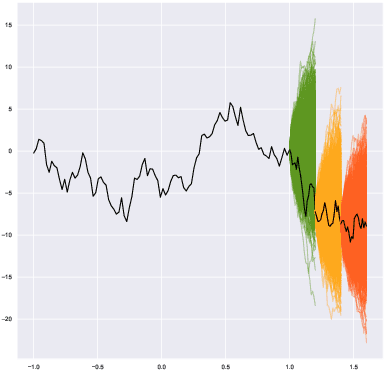
We introduce a universal class of geometric deep learning models, called metric hypertransformers (MHTs), capable of approximating any adapted map $F:\mathscr{X}^{\mathbb{Z}}\rightarrow \mathscr{Y}^{\mathbb{Z}}$ with approximable complexity, where $\mathscr{X}\subseteq \mathbb{R}^d$ and $\mathscr{Y}$ is any suitable metric space, and $\mathscr{X}^{\mathbb{Z}}$ (resp. $\mathscr{Y}^{\mathbb{Z}}$) capture all discrete-time paths on $\mathscr{X}$ (resp. $\mathscr{Y}$). Suitable spaces $\mathscr{Y}$ include various (adapted) Wasserstein spaces, all Fr\'{e}chet spaces admitting a Schauder basis, and a variety of Riemannian manifolds arising from information geometry. Even in the static case, where $f:\mathscr{X}\rightarrow \mathscr{Y}$ is a H\"{o}lder map, our results provide the first (quantitative) universal approximation theorem compatible with any such $\mathscr{X}$ and $\mathscr{Y}$. Our universal approximation theorems are quantitative, and they depend on the regularity of $F$, the choice of activation function, the metric entropy and diameter of $\mathscr{X}$, and on the regularity of the compact set of paths whereon the approximation is performed. Our guiding examples originate from mathematical finance. Notably, the MHT models introduced here are able to approximate a broad range of stochastic processes' kernels, including solutions to SDEs, many processes with arbitrarily long memory, and functions mapping sequential data to sequences of forward rate curves.