Robust Barycenter Estimation using Semi-Unbalanced Neural Optimal Transport

A common challenge in aggregating data from multiple sources can be formalized as an \textit{Optimal Transport} (OT) barycenter problem, which seeks to compute the average of probability distributions with respect to OT discrepancies. However, the presence of outliers and noise in the data measures can significantly hinder the performance of traditional statistical methods for estimating OT barycenters. To address this issue, we propose a novel, scalable approach for estimating the \textit{robust} continuous barycenter, leveraging the dual formulation of the \textit{(semi-)unbalanced} OT problem. To the best of our knowledge, this paper is the first attempt to develop an algorithm for robust barycenters under the continuous distribution setup. Our method is framed as a $\min$-$\max$ optimization problem and is adaptable to \textit{general} cost function. We rigorously establish the theoretical underpinnings of the proposed method and demonstrate its robustness to outliers and class imbalance through a number of illustrative experiments.

Estimating Barycenters of Distributions with Neural Optimal Transport

Given a collection of probability measures, a practitioner sometimes needs to find an "average" distribution which adequately aggregates reference distributions. A theoretically appealing notion of such an average is the Wasserstein barycenter, which is the primal focus of our work. By building upon the dual formulation of Optimal Transport (OT), we propose a new scalable approach for solving the Wasserstein barycenter problem. Our methodology is based on the recent Neural OT solver: it has bi-level adversarial learning objective and works for general cost functions. These are key advantages of our method, since the typical adversarial algorithms leveraging barycenter tasks utilize tri-level optimization and focus mostly on quadratic cost. We also establish theoretical error bounds for our proposed approach and showcase its applicability and effectiveness on illustrative scenarios and image data setups.

Energy-Guided Continuous Entropic Barycenter Estimation for General Costs

Optimal transport (OT) barycenters are a mathematically grounded way of averaging probability distributions while capturing their geometric properties. In short, the barycenter task is to take the average of a collection of probability distributions w.r.t. given OT discrepancies. We propose a novel algorithm for approximating the continuous Entropic OT (EOT) barycenter for arbitrary OT cost functions. Our approach is built upon the dual reformulation of the EOT problem based on weak OT, which has recently gained the attention of the ML community. Beyond its novelty, our method enjoys several advantageous properties: (i) we establish quality bounds for the recovered solution; (ii) this approach seemlessly interconnects with the Energy-Based Models (EBMs) learning procedure enabling the use of well-tuned algorithms for the problem of interest; (iii) it provides an intuitive optimization scheme avoiding min-max, reinforce and other intricate technical tricks. For validation, we consider several low-dimensional scenarios and image-space setups, including non-Euclidean cost functions. Furthermore, we investigate the practical task of learning the barycenter on an image manifold generated by a pretrained generative model, opening up new directions for real-world applications.

Building the Bridge of Schrödinger: A Continuous Entropic Optimal Transport Benchmark

Over the last several years, there has been a significant progress in developing neural solvers for the Schr\"odinger Bridge (SB) problem and applying them to generative modeling. This new research field is justifiably fruitful as it is interconnected with the practically well-performing diffusion models and theoretically-grounded entropic optimal transport (EOT). Still the area lacks non-trivial tests allowing a researcher to understand how well do the methods solve SB or its equivalent continuous EOT problem. We fill this gap and propose a novel way to create pairs of probability distributions for which the ground truth OT solution in known by the construction. Our methodology is generic and works for a wide range of OT formulations, in particular, it covers the EOT which is equivalent to SB (the main interest of our study). This development allows us to create continuous benchmark distributions with the known EOT and SB solution on high-dimensional spaces such as spaces of images. As an illustration, we use these benchmark pairs to test how well do existing neural EOT/SB solvers actually compute the EOT solution. The benchmark is available via the link: https://github.com/ngushchin/EntropicOTBenchmark.

Entropic Neural Optimal Transport via Diffusion Processes

We propose a novel neural algorithm for the fundamental problem of computing the entropic optimal transport (EOT) plan between probability distributions which are accessible by samples. Our algorithm is based on the saddle point reformulation of the dynamic version of EOT which is known as the Schr\"odinger Bridge problem. In contrast to the prior methods for large-scale EOT, our algorithm is end-to-end and consists of a single learning step, has fast inference procedure, and allows handling small values of the entropy regularization coefficient which is of particular importance in some applied problems. Empirically, we show the performance of the method on several large-scale EOT tasks.

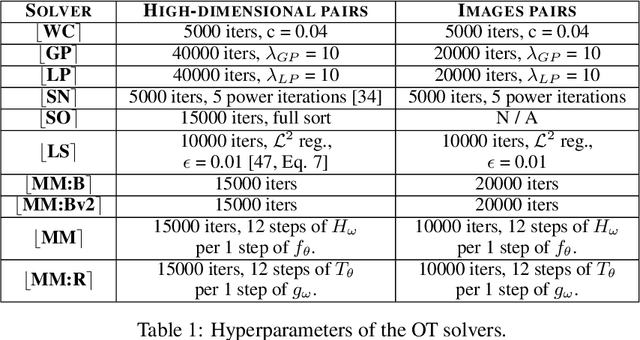
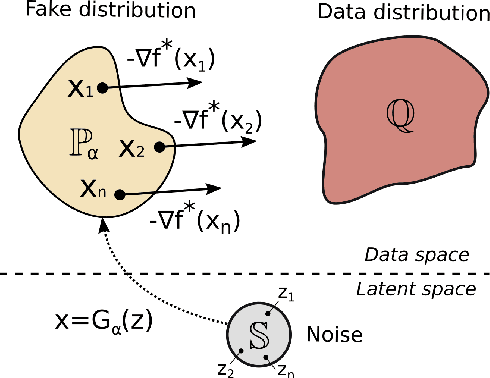
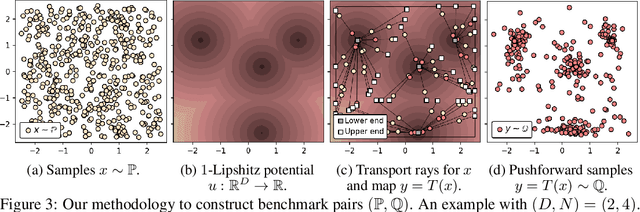
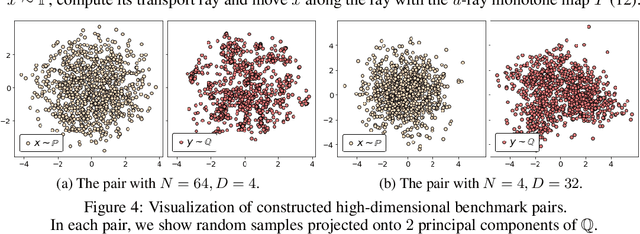
Kantorovich Strikes Back! Wasserstein GANs are not Optimal Transport?

Wasserstein Generative Adversarial Networks (WGANs) are the popular generative models built on the theory of Optimal Transport (OT) and the Kantorovich duality. Despite the success of WGANs, it is still unclear how well the underlying OT dual solvers approximate the OT cost (Wasserstein-1 distance, $\mathbb{W}_{1}$) and the OT gradient needed to update the generator. In this paper, we address these questions. We construct 1-Lipschitz functions and use them to build ray monotone transport plans. This strategy yields pairs of continuous benchmark distributions with the analytically known OT plan, OT cost and OT gradient in high-dimensional spaces such as spaces of images. We thoroughly evaluate popular WGAN dual form solvers (gradient penalty, spectral normalization, entropic regularization, etc.) using these benchmark pairs. Even though these solvers perform well in WGANs, none of them faithfully compute $\mathbb{W}_{1}$ in high dimensions. Nevertheless, many provide a meaningful approximation of the OT gradient. These observations suggest that these solvers should not be treated as good estimators of $\mathbb{W}_{1}$, but to some extent they indeed can be used in variational problems requiring the minimization of $\mathbb{W}_{1}$.