A Statistical Learning Perspective on Semi-dual Adversarial Neural Optimal Transport Solvers

Neural network based Optimal Transport (OT) is a recent and fruitful direction in the generative modeling community. It finds its applications in various fields such as domain translation, image super-resolution, computational biology and others. Among the existing approaches to OT, of considerable interest are adversarial minimax solvers based on semi-dual formulations of OT problems. While promising, these methods lack theoretical investigation from a statistical learning perspective. Our work fills this gap by establishing upper bounds on the generalization error of an approximate OT map recovered by the minimax quadratic OT solver. Importantly, the bounds we derive depend solely on some standard statistical and mathematical properties of the considered functional classes (neural networks). While our analysis focuses on the quadratic OT, we believe that similar bounds could be derived for more general OT formulations, paving the promising direction for future research.

Robust Barycenter Estimation using Semi-Unbalanced Neural Optimal Transport

A common challenge in aggregating data from multiple sources can be formalized as an \textit{Optimal Transport} (OT) barycenter problem, which seeks to compute the average of probability distributions with respect to OT discrepancies. However, the presence of outliers and noise in the data measures can significantly hinder the performance of traditional statistical methods for estimating OT barycenters. To address this issue, we propose a novel, scalable approach for estimating the \textit{robust} continuous barycenter, leveraging the dual formulation of the \textit{(semi-)unbalanced} OT problem. To the best of our knowledge, this paper is the first attempt to develop an algorithm for robust barycenters under the continuous distribution setup. Our method is framed as a $\min$-$\max$ optimization problem and is adaptable to \textit{general} cost function. We rigorously establish the theoretical underpinnings of the proposed method and demonstrate its robustness to outliers and class imbalance through a number of illustrative experiments.

Estimating Barycenters of Distributions with Neural Optimal Transport

Given a collection of probability measures, a practitioner sometimes needs to find an "average" distribution which adequately aggregates reference distributions. A theoretically appealing notion of such an average is the Wasserstein barycenter, which is the primal focus of our work. By building upon the dual formulation of Optimal Transport (OT), we propose a new scalable approach for solving the Wasserstein barycenter problem. Our methodology is based on the recent Neural OT solver: it has bi-level adversarial learning objective and works for general cost functions. These are key advantages of our method, since the typical adversarial algorithms leveraging barycenter tasks utilize tri-level optimization and focus mostly on quadratic cost. We also establish theoretical error bounds for our proposed approach and showcase its applicability and effectiveness on illustrative scenarios and image data setups.

Energy-Guided Continuous Entropic Barycenter Estimation for General Costs

Optimal transport (OT) barycenters are a mathematically grounded way of averaging probability distributions while capturing their geometric properties. In short, the barycenter task is to take the average of a collection of probability distributions w.r.t. given OT discrepancies. We propose a novel algorithm for approximating the continuous Entropic OT (EOT) barycenter for arbitrary OT cost functions. Our approach is built upon the dual reformulation of the EOT problem based on weak OT, which has recently gained the attention of the ML community. Beyond its novelty, our method enjoys several advantageous properties: (i) we establish quality bounds for the recovered solution; (ii) this approach seemlessly interconnects with the Energy-Based Models (EBMs) learning procedure enabling the use of well-tuned algorithms for the problem of interest; (iii) it provides an intuitive optimization scheme avoiding min-max, reinforce and other intricate technical tricks. For validation, we consider several low-dimensional scenarios and image-space setups, including non-Euclidean cost functions. Furthermore, we investigate the practical task of learning the barycenter on an image manifold generated by a pretrained generative model, opening up new directions for real-world applications.

Building the Bridge of Schrödinger: A Continuous Entropic Optimal Transport Benchmark

Over the last several years, there has been a significant progress in developing neural solvers for the Schr\"odinger Bridge (SB) problem and applying them to generative modeling. This new research field is justifiably fruitful as it is interconnected with the practically well-performing diffusion models and theoretically-grounded entropic optimal transport (EOT). Still the area lacks non-trivial tests allowing a researcher to understand how well do the methods solve SB or its equivalent continuous EOT problem. We fill this gap and propose a novel way to create pairs of probability distributions for which the ground truth OT solution in known by the construction. Our methodology is generic and works for a wide range of OT formulations, in particular, it covers the EOT which is equivalent to SB (the main interest of our study). This development allows us to create continuous benchmark distributions with the known EOT and SB solution on high-dimensional spaces such as spaces of images. As an illustration, we use these benchmark pairs to test how well do existing neural EOT/SB solvers actually compute the EOT solution. The benchmark is available via the link: https://github.com/ngushchin/EntropicOTBenchmark.

Energy-guided Entropic Neural Optimal Transport

Energy-Based Models (EBMs) are known in the Machine Learning community for the decades. Since the seminal works devoted to EBMs dating back to the noughties there have been appearing a lot of efficient methods which solve the generative modelling problem by means of energy potentials (unnormalized likelihood functions). In contrast, the realm of Optimal Transport (OT) and, in particular, neural OT solvers is much less explored and limited by few recent works (excluding WGAN based approaches which utilize OT as a loss function and do not model OT maps themselves). In our work, we bridge the gap between EBMs and Entropy-regularized OT. We present the novel methodology which allows utilizing the recent developments and technical improvements of the former in order to enrich the latter. We validate the applicability of our method on toy 2D scenarios as well as standard unpaired image-to-image translation problems. For the sake of simplicity, we choose simple short- and long- run EBMs as a backbone of our Energy-guided Entropic OT method, leaving the application of more sophisticated EBMs for future research.

Large-Scale Wasserstein Gradient Flows

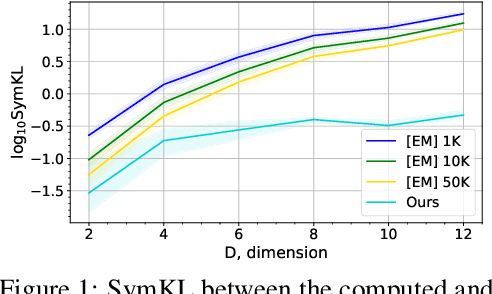
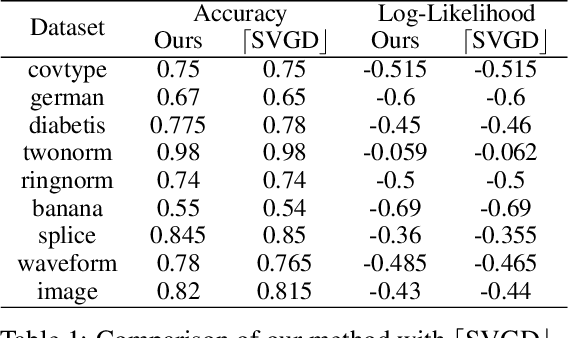
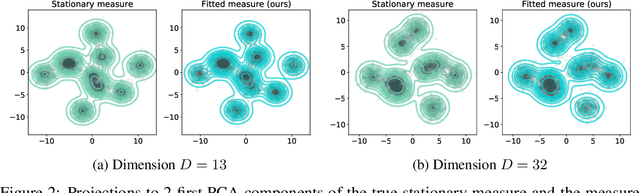
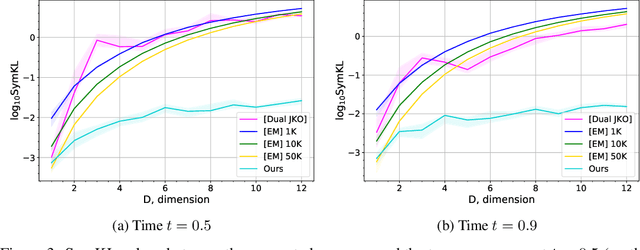
Wasserstein gradient flows provide a powerful means of understanding and solving many diffusion equations. Specifically, Fokker-Planck equations, which model the diffusion of probability measures, can be understood as gradient descent over entropy functionals in Wasserstein space. This equivalence, introduced by Jordan, Kinderlehrer and Otto, inspired the so-called JKO scheme to approximate these diffusion processes via an implicit discretization of the gradient flow in Wasserstein space. Solving the optimization problem associated to each JKO step, however, presents serious computational challenges. We introduce a scalable method to approximate Wasserstein gradient flows, targeted to machine learning applications. Our approach relies on input-convex neural networks (ICNNs) to discretize the JKO steps, which can be optimized by stochastic gradient descent. Unlike previous work, our method does not require domain discretization or particle simulation. As a result, we can sample from the measure at each time step of the diffusion and compute its probability density. We demonstrate our algorithm's performance by computing diffusions following the Fokker-Planck equation and apply it to unnormalized density sampling as well as nonlinear filtering.