Multi-View Learning with Context-Guided Receptance for Image Denoising

Image denoising is essential in low-level vision applications such as photography and automated driving. Existing methods struggle with distinguishing complex noise patterns in real-world scenes and consume significant computational resources due to reliance on Transformer-based models. In this work, the Context-guided Receptance Weighted Key-Value (\M) model is proposed, combining enhanced multi-view feature integration with efficient sequence modeling. Our approach introduces the Context-guided Token Shift (CTS) paradigm, which effectively captures local spatial dependencies and enhance the model's ability to model real-world noise distributions. Additionally, the Frequency Mix (FMix) module extracting frequency-domain features is designed to isolate noise in high-frequency spectra, and is integrated with spatial representations through a multi-view learning process. To improve computational efficiency, the Bidirectional WKV (BiWKV) mechanism is adopted, enabling full pixel-sequence interaction with linear complexity while overcoming the causal selection constraints. The model is validated on multiple real-world image denoising datasets, outperforming the existing state-of-the-art methods quantitatively and reducing inference time up to 40\%. Qualitative results further demonstrate the ability of our model to restore fine details in various scenes.

Using the Split Bregman Algorithm to Solve the Self-Repelling Snake Model

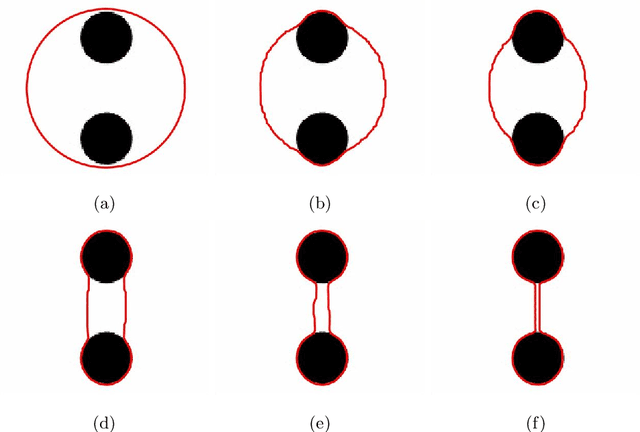
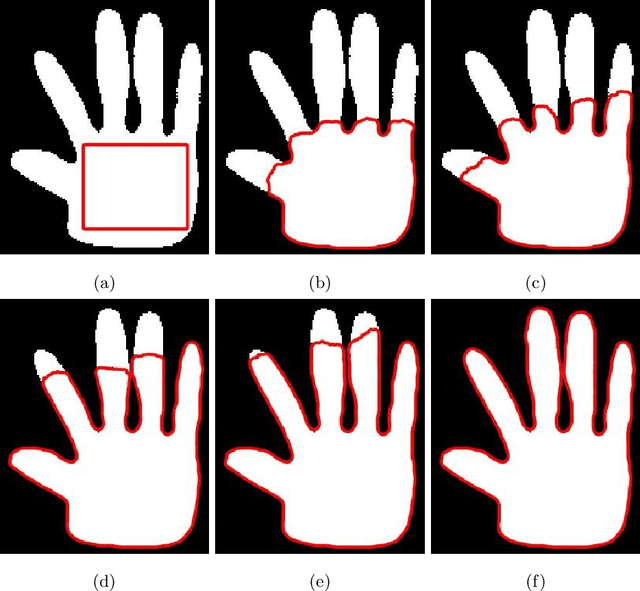
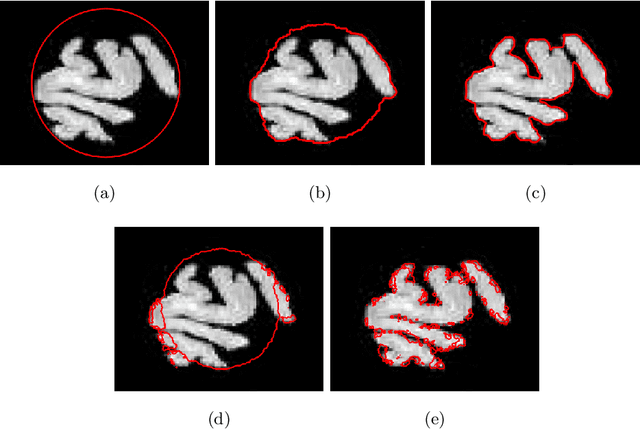
Preserving the contour topology during image segmentation is useful in manypractical scenarios. By keeping the contours isomorphic, it is possible to pre-vent over-segmentation and under-segmentation, as well as to adhere to giventopologies. The self-repelling snake model (SR) is a variational model thatpreserves contour topology by combining a non-local repulsion term with thegeodesic active contour model (GAC). The SR is traditionally solved using theadditive operator splitting (AOS) scheme. Although this solution is stable, thememory requirement grows quickly as the image size increases. In our paper,we propose an alternative solution to the SR using the Split Bregman method.Our algorithm breaks the problem down into simpler subproblems to use lower-order evolution equations and approximation schemes. The memory usage issignificantly reduced as a result. Experiments show comparable performance to the original algorithm with shorter iteration times.