Universal Domain Adaptation Benchmark for Time Series Data Representation

Deep learning models have significantly improved the ability to detect novelties in time series (TS) data. This success is attributed to their strong representation capabilities. However, due to the inherent variability in TS data, these models often struggle with generalization and robustness. To address this, a common approach is to perform Unsupervised Domain Adaptation, particularly Universal Domain Adaptation (UniDA), to handle domain shifts and emerging novel classes. While extensively studied in computer vision, UniDA remains underexplored for TS data. This work provides a comprehensive implementation and comparison of state-of-the-art TS backbones in a UniDA framework. We propose a reliable protocol to evaluate their robustness and generalization across different domains. The goal is to provide practitioners with a framework that can be easily extended to incorporate future advancements in UniDA and TS architectures. Our results highlight the critical influence of backbone selection in UniDA performance and enable a robustness analysis across various datasets and architectures.

PatchTrAD: A Patch-Based Transformer focusing on Patch-Wise Reconstruction Error for Time Series Anomaly Detection

Time series anomaly detection (TSAD) focuses on identifying whether observations in streaming data deviate significantly from normal patterns. With the prevalence of connected devices, anomaly detection on time series has become paramount, as it enables real-time monitoring and early detection of irregular behaviors across various application domains. In this work, we introduce PatchTrAD, a Patch-based Transformer model for time series anomaly detection. Our approach leverages a Transformer encoder along with the use of patches under a reconstructionbased framework for anomaly detection. Empirical evaluations on multiple benchmark datasets show that PatchTrAD is on par, in terms of detection performance, with state-of-the-art deep learning models for anomaly detection while being time efficient during inference.

Optimal Transport and Adaptive Thresholding for Universal Domain Adaptation on Time Series

Universal Domain Adaptation (UniDA) aims to transfer knowledge from a labeled source domain to an unlabeled target domain, even when their classes are not fully shared. Few dedicated UniDA methods exist for Time Series (TS), which remains a challenging case. In general, UniDA approaches align common class samples and detect unknown target samples from emerging classes. Such detection often results from thresholding a discriminability metric. The threshold value is typically either a fine-tuned hyperparameter or a fixed value, which limits the ability of the model to adapt to new data. Furthermore, discriminability metrics exhibit overconfidence for unknown samples, leading to misclassifications. This paper introduces UniJDOT, an optimal-transport-based method that accounts for the unknown target samples in the transport cost. Our method also proposes a joint decision space to improve the discriminability of the detection module. In addition, we use an auto-thresholding algorithm to reduce the dependence on fixed or fine-tuned thresholds. Finally, we rely on a Fourier transform-based layer inspired by the Fourier Neural Operator for better TS representation. Experiments on TS benchmarks demonstrate the discriminability, robustness, and state-of-the-art performance of UniJDOT.

Gaussian-Smoothed Sliced Probability Divergences

Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown that it provides performances similar to its non-smoothed (non-private) counterpart. However, the computationaland statistical properties of such a metric have not yet been well-established. This work investigates the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian-smoothed sliced divergences. We first show that smoothing and slicing preserve the metric property and the weak topology. To study the sample complexity of such divergences, we then introduce $\hat{\hat\mu}_{n}$ the double empirical distribution for the smoothed-projected $\mu$. The distribution $\hat{\hat\mu}_{n}$ is a result of a double sampling process: one from sampling according to the origin distribution $\mu$ and the second according to the convolution of the projection of $\mu$ on the unit sphere and the Gaussian smoothing. We particularly focus on the Gaussian smoothed sliced Wasserstein distance and prove that it converges with a rate $O(n^{-1/2})$. We also derive other properties, including continuity, of different divergences with respect to the smoothing parameter. We support our theoretical findings with empirical studies in the context of privacy-preserving domain adaptation.

Adversarial Semi-Supervised Domain Adaptation for Semantic Segmentation: A New Role for Labeled Target Samples

Adversarial learning baselines for domain adaptation (DA) approaches in the context of semantic segmentation are under explored in semi-supervised framework. These baselines involve solely the available labeled target samples in the supervision loss. In this work, we propose to enhance their usefulness on both semantic segmentation and the single domain classifier neural networks. We design new training objective losses for cases when labeled target data behave as source samples or as real target samples. The underlying rationale is that considering the set of labeled target samples as part of source domain helps reducing the domain discrepancy and, hence, improves the contribution of the adversarial loss. To support our approach, we consider a complementary method that mixes source and labeled target data, then applies the same adaptation process. We further propose an unsupervised selection procedure using entropy to optimize the choice of labeled target samples for adaptation. We illustrate our findings through extensive experiments on the benchmarks GTA5, SYNTHIA, and Cityscapes. The empirical evaluation highlights competitive performance of our proposed approach.

Fast Optimal Transport through Sliced Wasserstein Generalized Geodesics

Wasserstein distance (WD) and the associated optimal transport plan have been proven useful in many applications where probability measures are at stake. In this paper, we propose a new proxy of the squared WD, coined min-SWGG, that is based on the transport map induced by an optimal one-dimensional projection of the two input distributions. We draw connections between min-SWGG and Wasserstein generalized geodesics in which the pivot measure is supported on a line. We notably provide a new closed form for the exact Wasserstein distance in the particular case of one of the distributions supported on a line allowing us to derive a fast computational scheme that is amenable to gradient descent optimization. We show that min-SWGG is an upper bound of WD and that it has a complexity similar to as Sliced-Wasserstein, with the additional feature of providing an associated transport plan. We also investigate some theoretical properties such as metricity, weak convergence, computational and topological properties. Empirical evidences support the benefits of min-SWGG in various contexts, from gradient flows, shape matching and image colorization, among others.

Physically-admissible polarimetric data augmentation for road-scene analysis

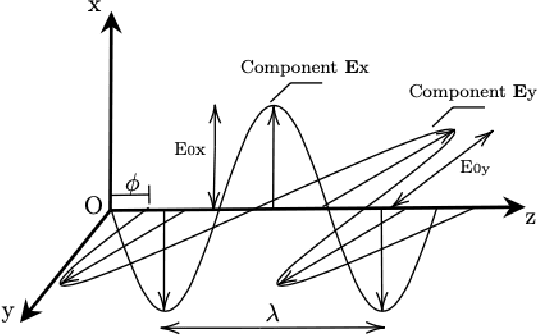
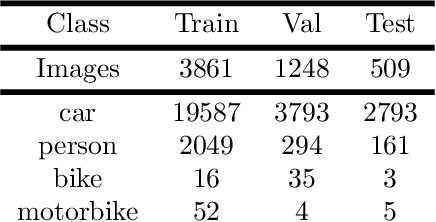
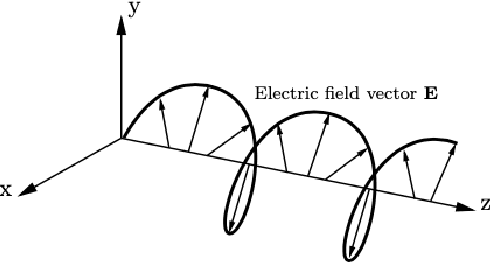
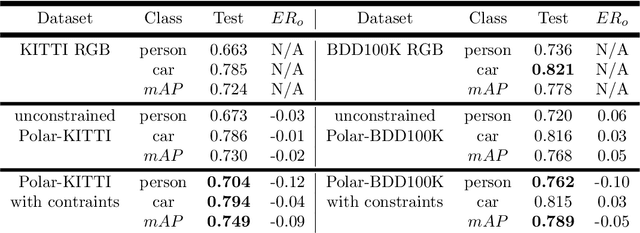
Polarimetric imaging, along with deep learning, has shown improved performances on different tasks including scene analysis. However, its robustness may be questioned because of the small size of the training datasets. Though the issue could be solved by data augmentation, polarization modalities are subject to physical feasibility constraints unaddressed by classical data augmentation techniques. To address this issue, we propose to use CycleGAN, an image translation technique based on deep generative models that solely relies on unpaired data, to transfer large labeled road scene datasets to the polarimetric domain. We design several auxiliary loss terms that, alongside the CycleGAN losses, deal with the physical constraints of polarimetric images. The efficiency of this solution is demonstrated on road scene object detection tasks where generated realistic polarimetric images allow to improve performances on cars and pedestrian detection up to 9%. The resulting constrained CycleGAN is publicly released, allowing anyone to generate their own polarimetric images.

Statistical and Topological Properties of Gaussian Smoothed Sliced Probability Divergences

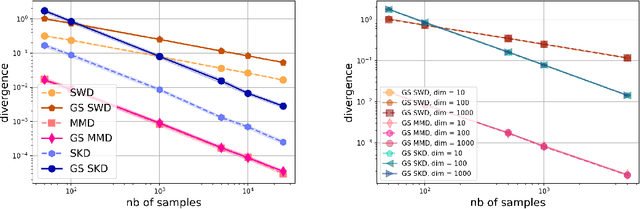
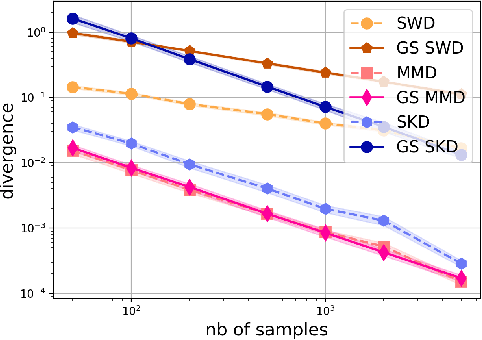
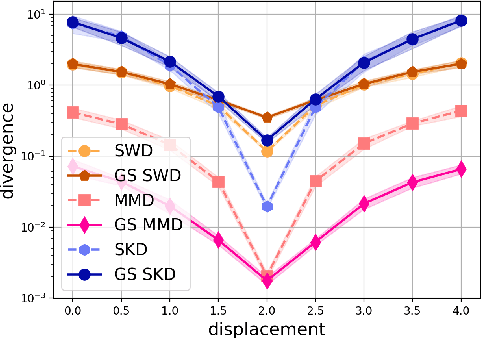
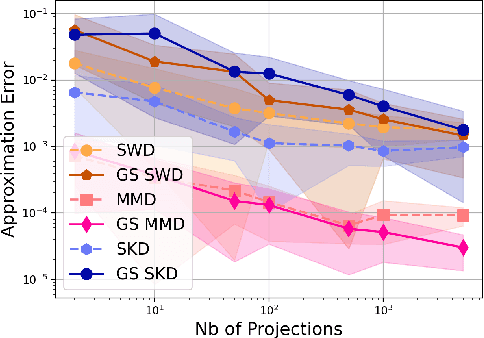
Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown, in applications such as domain adaptation, to provide performances similar to its non-private (non-smoothed) counterpart. However, the computational and statistical properties of such a metric is not yet been well-established. In this paper, we analyze the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian smoothed sliced divergences. We show that smoothing and slicing preserve the metric property and the weak topology. We also provide results on the sample complexity of such divergences. Since, the privacy level depends on the amount of Gaussian smoothing, we analyze the impact of this parameter on the divergence. We support our theoretical findings with empirical studies of Gaussian smoothed and sliced version of Wassertein distance, Sinkhorn divergence and maximum mean discrepancy (MMD). In the context of privacy-preserving domain adaptation, we confirm that those Gaussian smoothed sliced Wasserstein and MMD divergences perform very well while ensuring data privacy.

Unbalanced Optimal Transport through Non-negative Penalized Linear Regression

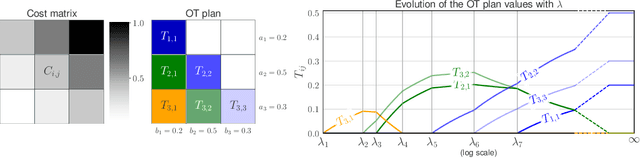
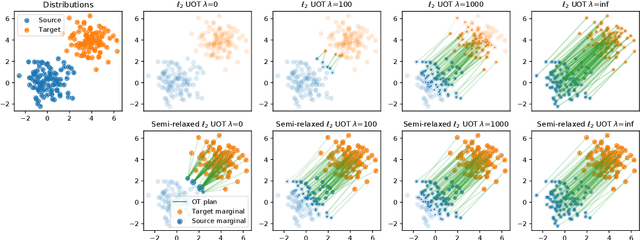
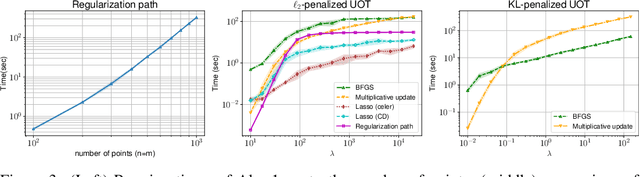
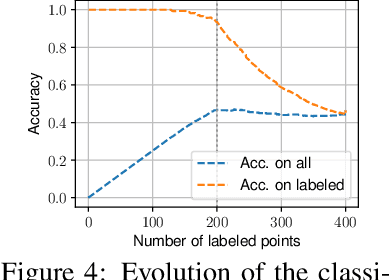
This paper addresses the problem of Unbalanced Optimal Transport (UOT) in which the marginal conditions are relaxed (using weighted penalties in lieu of equality) and no additional regularization is enforced on the OT plan. In this context, we show that the corresponding optimization problem can be reformulated as a non-negative penalized linear regression problem. This reformulation allows us to propose novel algorithms inspired from inverse problems and nonnegative matrix factorization. In particular, we consider majorization-minimization which leads in our setting to efficient multiplicative updates for a variety of penalties. Furthermore, we derive for the first time an efficient algorithm to compute the regularization path of UOT with quadratic penalties. The proposed algorithm provides a continuity of piece-wise linear OT plans converging to the solution of balanced OT (corresponding to infinite penalty weights). We perform several numerical experiments on simulated and real data illustrating the new algorithms, and provide a detailed discussion about more sophisticated optimization tools that can further be used to solve OT problems thanks to our reformulation.

Distributional Sliced Embedding Discrepancy for Incomparable Distributions

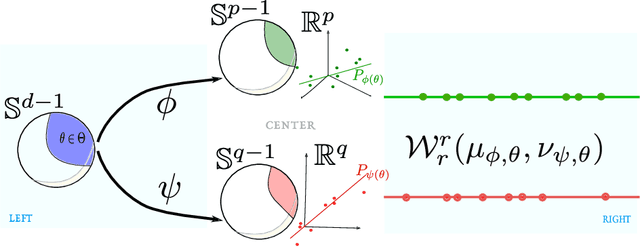
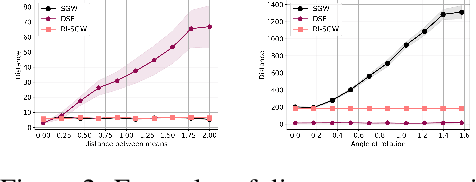
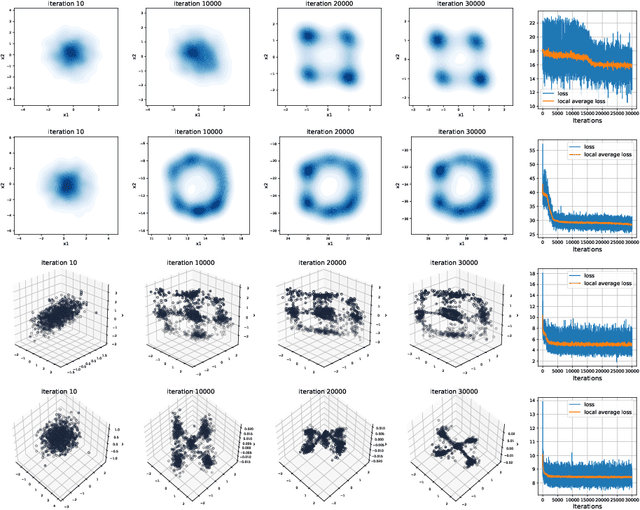
Gromov-Wasserstein (GW) distance is a key tool for manifold learning and cross-domain learning, allowing the comparison of distributions that do not live in the same metric space. Because of its high computational complexity, several approximate GW distances have been proposed based on entropy regularization or on slicing, and one-dimensional GW computation. In this paper, we propose a novel approach for comparing two incomparable distributions, that hinges on the idea of distributional slicing, embeddings, and on computing the closed-form Wasserstein distance between the sliced distributions. We provide a theoretical analysis of this new divergence, called distributional sliced embedding (DSE) discrepancy, and we show that it preserves several interesting properties of GW distance including rotation-invariance. We show that the embeddings involved in DSE can be efficiently learned. Finally, we provide a large set of experiments illustrating the behavior of DSE as a divergence in the context of generative modeling and in query framework.