Stability Analysis of Physics-Informed Neural Networks for Stiff Linear Differential Equations

We present a stability analysis of Physics-Informed Neural Networks (PINNs) coupled with random projections, for the numerical solution of (stiff) linear differential equations. For our analysis, we consider systems of linear ODEs, and linear parabolic PDEs. We prove that properly designed PINNs offer consistent and asymptotically stable numerical schemes, thus convergent schemes. In particular, we prove that multi-collocation random projection PINNs guarantee asymptotic stability for very high stiffness and that single-collocation PINNs are $A$-stable. To assess the performance of the PINNs in terms of both numerical approximation accuracy and computational cost, we compare it with other implicit schemes and in particular backward Euler, the midpoint, trapezoidal (Crank-Nikolson), the 2-stage Gauss scheme and the 2 and 3 stages Radau schemes. We show that the proposed PINNs outperform the above traditional schemes, in both numerical approximation accuracy and importantly computational cost, for a wide range of step sizes.

RandONet: Shallow-Networks with Random Projections for learning linear and nonlinear operators

Deep Operator Networks (DeepOnets) have revolutionized the domain of scientific machine learning for the solution of the inverse problem for dynamical systems. However, their implementation necessitates optimizing a high-dimensional space of parameters and hyperparameters. This fact, along with the requirement of substantial computational resources, poses a barrier to achieving high numerical accuracy. Here, inpsired by DeepONets and to address the above challenges, we present Random Projection-based Operator Networks (RandONets): shallow networks with random projections that learn linear and nonlinear operators. The implementation of RandONets involves: (a) incorporating random bases, thus enabling the use of shallow neural networks with a single hidden layer, where the only unknowns are the output weights of the network's weighted inner product; this reduces dramatically the dimensionality of the parameter space; and, based on this, (b) using established least-squares solvers (e.g., Tikhonov regularization and preconditioned QR decomposition) that offer superior numerical approximation properties compared to other optimization techniques used in deep-learning. In this work, we prove the universal approximation accuracy of RandONets for approximating nonlinear operators and demonstrate their efficiency in approximating linear nonlinear evolution operators (right-hand-sides (RHS)) with a focus on PDEs. We show, that for this particular task, RandONets outperform, both in terms of numerical approximation accuracy and computational cost, the ``vanilla" DeepOnets.

Nonlinear Discrete-Time Observers with Physics-Informed Neural Networks

We use Physics-Informed Neural Networks (PINNs) to solve the discrete-time nonlinear observer state estimation problem. Integrated within a single-step exact observer linearization framework, the proposed PINN approach aims at learning a nonlinear state transformation map by solving a system of inhomogeneous functional equations. The performance of the proposed PINN approach is assessed via two illustrative case studies for which the observer linearizing transformation map can be derived analytically. We also perform an uncertainty quantification analysis for the proposed PINN scheme and we compare it with conventional power-series numerical implementations, which rely on the computation of a power series solution.

Random Projection Neural Networks of Best Approximation: Convergence theory and practical applications

We investigate the concept of Best Approximation for Feedforward Neural Networks (FNN) and explore their convergence properties through the lens of Random Projection (RPNNs). RPNNs have predetermined and fixed, once and for all, internal weights and biases, offering computational efficiency. We demonstrate that there exists a choice of external weights, for any family of such RPNNs, with non-polynomial infinitely differentiable activation functions, that exhibit an exponential convergence rate when approximating any infinitely differentiable function. For illustration purposes, we test the proposed RPNN-based function approximation, with parsimoniously chosen basis functions, across five benchmark function approximation problems. Results show that RPNNs achieve comparable performance to established methods such as Legendre Polynomials, highlighting their potential for efficient and accurate function approximation.

Tasks Makyth Models: Machine Learning Assisted Surrogates for Tipping Points

We present a machine learning (ML)-assisted framework bridging manifold learning, neural networks, Gaussian processes, and Equation-Free multiscale modeling, for (a) detecting tipping points in the emergent behavior of complex systems, and (b) characterizing probabilities of rare events (here, catastrophic shifts) near them. Our illustrative example is an event-driven, stochastic agent-based model (ABM) describing the mimetic behavior of traders in a simple financial market. Given high-dimensional spatiotemporal data -- generated by the stochastic ABM -- we construct reduced-order models for the emergent dynamics at different scales: (a) mesoscopic Integro-Partial Differential Equations (IPDEs); and (b) mean-field-type Stochastic Differential Equations (SDEs) embedded in a low-dimensional latent space, targeted to the neighborhood of the tipping point. We contrast the uses of the different models and the effort involved in learning them.

Slow Invariant Manifolds of Singularly Perturbed Systems via Physics-Informed Machine Learning

We present a physics-informed machine-learning (PIML) approach for the approximation of slow invariant manifolds (SIMs) of singularly perturbed systems, providing functionals in an explicit form that facilitate the construction and numerical integration of reduced order models (ROMs). The proposed scheme solves a partial differential equation corresponding to the invariance equation (IE) within the Geometric Singular Perturbation Theory (GSPT) framework. For the solution of the IE, we used two neural network structures, namely feedforward neural networks (FNNs), and random projection neural networks (RPNNs), with symbolic differentiation for the computation of the gradients required for the learning process. The efficiency of our PIML method is assessed via three benchmark problems, namely the Michaelis-Menten, the target mediated drug disposition reaction mechanism, and the 3D Sel'kov model. We show that the proposed PIML scheme provides approximations, of equivalent or even higher accuracy, than those provided by other traditional GSPT-based methods, and importantly, for any practical purposes, it is not affected by the magnitude of the perturbation parameter. This is of particular importance, as there are many systems for which the gap between the fast and slow timescales is not that big, but still ROMs can be constructed. A comparison of the computational costs between symbolic, automatic and numerical approximation of the required derivatives in the learning process is also provided.

Discrete-Time Nonlinear Feedback Linearization via Physics-Informed Machine Learning

We present a physics-informed machine learning (PIML) scheme for the feedback linearization of nonlinear discrete-time dynamical systems. The PIML finds the nonlinear transformation law, thus ensuring stability via pole placement, in one step. In order to facilitate convergence in the presence of steep gradients in the nonlinear transformation law, we address a greedy-wise training procedure. We assess the performance of the proposed PIML approach via a benchmark nonlinear discrete map for which the feedback linearization transformation law can be derived analytically; the example is characterized by steep gradients, due to the presence of singularities, in the domain of interest. We show that the proposed PIML outperforms, in terms of numerical approximation accuracy, the traditional numerical implementation, which involves the construction--and the solution in terms of the coefficients of a power-series expansion--of a system of homological equations as well as the implementation of the PIML in the entire domain, thus highlighting the importance of continuation techniques in the training procedure of PIML.

Parsimonious Physics-Informed Random Projection Neural Networks for Initial-Value Problems of ODEs and index-1 DAEs

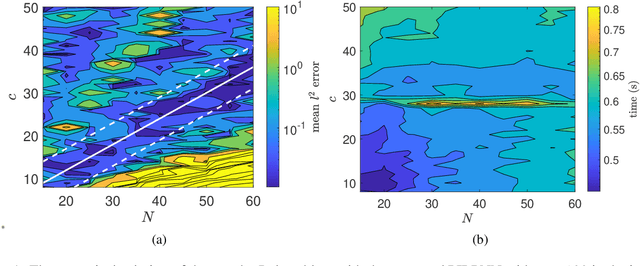
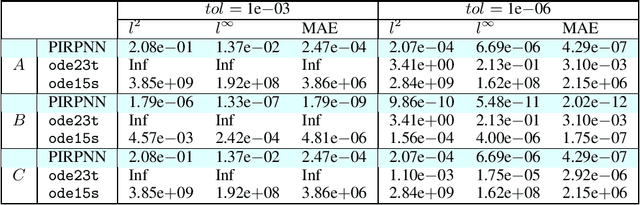
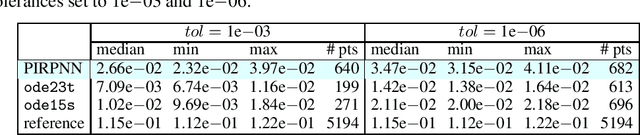
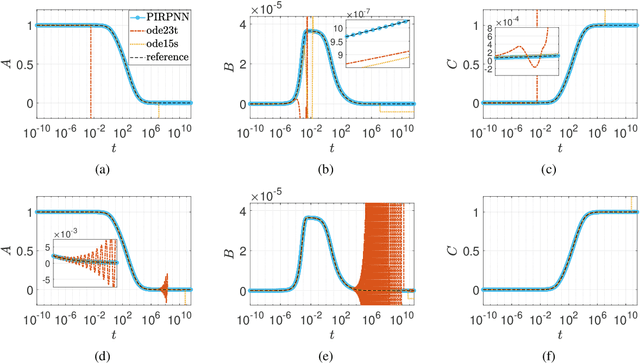
We address a physics-informed neural network based on the concept of random projections for the numerical solution of IVPs of nonlinear ODEs in linear-implicit form and index-1 DAEs, which may also arise from the spatial discretization of PDEs. The scheme has a single hidden layer with appropriately randomly parametrized Gaussian kernels and a linear output layer, while the internal weights are fixed to ones. The unknown weights between the hidden and output layer are computed by Newton's iterations, using the Moore-Penrose pseudoinverse for low to medium, and sparse QR decomposition with regularization for medium to large scale systems. To deal with stiffness and sharp gradients, we propose a variable step size scheme for adjusting the interval of integration and address a continuation method for providing good initial guesses for the Newton iterations. Based on previous works on random projections, we prove the approximation capability of the scheme for ODEs in the canonical form and index-1 DAEs in the semiexplicit form. The optimal bounds of the uniform distribution are parsimoniously chosen based on the bias-variance trade-off. The performance of the scheme is assessed through seven benchmark problems: four index-1 DAEs, the Robertson model, a model of five DAEs describing the motion of a bead, a model of six DAEs describing a power discharge control problem, the chemical Akzo Nobel problem and three stiff problems, the Belousov-Zhabotinsky, the Allen-Cahn PDE and the Kuramoto-Sivashinsky PDE. The efficiency of the scheme is compared with three solvers ode23t, ode23s, ode15s of the MATLAB ODE suite. Our results show that the proposed scheme outperforms the stiff solvers in several cases, especially in regimes where high stiffness or sharp gradients arise in terms of numerical accuracy, while the computational costs are for any practical purposes comparable.

Constructing coarse-scale bifurcation diagrams from spatio-temporal observations of microscopic simulations: A parsimonious machine learning approach

We address a three-tier data-driven approach to solve the inverse problem in complex systems modelling from spatio-temporal data produced by microscopic simulators using machine learning. In the first step, we exploit manifold learning and in particular parsimonious Diffusion Maps using leave-one-out cross-validation (LOOCV) to both identify the intrinsic dimension of the manifold where the emergent dynamics evolve and for feature selection over the parametric space. In the second step, based on the selected features, we learn the right-hand-side of the effective partial differential equations (PDEs) using two machine learning schemes, namely shallow Feedforward Neural Networks (FNNs) with two hidden layers and single-layer Random Projection Networks(RPNNs) which basis functions are constructed using an appropriate random sampling approach. Finally, based on the learned black-box PDE model, we construct the corresponding bifurcation diagram, thus exploiting the numerical bifurcation analysis toolkit. For our illustrations, we implemented the proposed method to construct the one-parameter bifurcation diagram of the 1D FitzHugh-Nagumo PDEs from data generated by $D1Q3$ Lattice Boltzmann simulations. The proposed method was quite effective in terms of numerical accuracy regarding the construction of the coarse-scale bifurcation diagram. Furthermore, the proposed RPNN scheme was $\sim$ 20 to 30 times less costly regarding the training phase than the traditional shallow FNNs, thus arising as a promising alternative to deep learning for solving the inverse problem for high-dimensional PDEs.