Assimilative Causal Inference

Causal inference determines cause-and-effect relationships between variables and has broad applications across disciplines. Traditional time-series methods often reveal causal links only in a time-averaged sense, while ensemble-based information transfer approaches detect the time evolution of short-term causal relationships but are typically limited to low-dimensional systems. In this paper, a new causal inference framework, called assimilative causal inference (ACI), is developed. Fundamentally different from the state-of-the-art methods, ACI uses a dynamical system and a single realization of a subset of the state variables to identify instantaneous causal relationships and the dynamic evolution of the associated causal influence range (CIR). Instead of quantifying how causes influence effects as done traditionally, ACI solves an inverse problem via Bayesian data assimilation, thus tracing causes backward from observed effects with an implicit Bayesian hypothesis. Causality is determined by assessing whether incorporating the information of the effect variables reduces the uncertainty in recovering the potential cause variables. ACI has several desirable features. First, it captures the dynamic interplay of variables, where their roles as causes and effects can shift repeatedly over time. Second, a mathematically justified objective criterion determines the CIR without empirical thresholds. Third, ACI is scalable to high-dimensional problems by leveraging computationally efficient Bayesian data assimilation techniques. Finally, ACI applies to short time series and incomplete datasets. Notably, ACI does not require observations of candidate causes, which is a key advantage since potential drivers are often unknown or unmeasured. The effectiveness of ACI is demonstrated by complex dynamical systems showcasing intermittency and extreme events.

On the emergence of numerical instabilities in Next Generation Reservoir Computing

Next Generation Reservoir Computing (NGRC) is a low-cost machine learning method for forecasting chaotic time series from data. However, ensuring the dynamical stability of NGRC models during autonomous prediction remains a challenge. In this work, we uncover a key connection between the numerical conditioning of the NGRC feature matrix -- formed by polynomial evaluations on time-delay coordinates -- and the long-term NGRC dynamics. Merging tools from numerical linear algebra and ergodic theory of dynamical systems, we systematically study how the feature matrix conditioning varies across hyperparameters. We demonstrate that the NGRC feature matrix tends to be ill-conditioned for short time lags and high-degree polynomials. Ill-conditioning amplifies sensitivity to training data perturbations, which can produce unstable NGRC dynamics. We evaluate the impact of different numerical algorithms (Cholesky, SVD, and LU) for solving the regularized least-squares problem.

Kolmogorov-Arnold Network Autoencoders

Deep learning models have revolutionized various domains, with Multi-Layer Perceptrons (MLPs) being a cornerstone for tasks like data regression and image classification. However, a recent study has introduced Kolmogorov-Arnold Networks (KANs) as promising alternatives to MLPs, leveraging activation functions placed on edges rather than nodes. This structural shift aligns KANs closely with the Kolmogorov-Arnold representation theorem, potentially enhancing both model accuracy and interpretability. In this study, we explore the efficacy of KANs in the context of data representation via autoencoders, comparing their performance with traditional Convolutional Neural Networks (CNNs) on the MNIST, SVHN, and CIFAR-10 datasets. Our results demonstrate that KAN-based autoencoders achieve competitive performance in terms of reconstruction accuracy, thereby suggesting their viability as effective tools in data analysis tasks.

Stability Analysis of Physics-Informed Neural Networks for Stiff Linear Differential Equations

We present a stability analysis of Physics-Informed Neural Networks (PINNs) coupled with random projections, for the numerical solution of (stiff) linear differential equations. For our analysis, we consider systems of linear ODEs, and linear parabolic PDEs. We prove that properly designed PINNs offer consistent and asymptotically stable numerical schemes, thus convergent schemes. In particular, we prove that multi-collocation random projection PINNs guarantee asymptotic stability for very high stiffness and that single-collocation PINNs are $A$-stable. To assess the performance of the PINNs in terms of both numerical approximation accuracy and computational cost, we compare it with other implicit schemes and in particular backward Euler, the midpoint, trapezoidal (Crank-Nikolson), the 2-stage Gauss scheme and the 2 and 3 stages Radau schemes. We show that the proposed PINNs outperform the above traditional schemes, in both numerical approximation accuracy and importantly computational cost, for a wide range of step sizes.

Entropic Regression DMD (ERDMD) Discovers Informative Sparse and Nonuniformly Time Delayed Models

In this work, we present a method which determines optimal multi-step dynamic mode decomposition (DMD) models via entropic regression, which is a nonlinear information flow detection algorithm. Motivated by the higher-order DMD (HODMD) method of \cite{clainche}, and the entropic regression (ER) technique for network detection and model construction found in \cite{bollt, bollt2}, we develop a method that we call ERDMD that produces high fidelity time-delay DMD models that allow for nonuniform time space, and the time spacing is discovered by consider most informativity based on ER. These models are shown to be highly efficient and robust. We test our method over several data sets generated by chaotic attractors and show that we are able to build excellent reconstructions using relatively minimal models. We likewise are able to better identify multiscale features via our models which enhances the utility of dynamic mode decomposition.

On Learning what to Learn: heterogeneous observations of dynamics and establishing (possibly causal) relations among them

Before we attempt to learn a function between two (sets of) observables of a physical process, we must first decide what the inputs and what the outputs of the desired function are going to be. Here we demonstrate two distinct, data-driven ways of initially deciding ``the right quantities'' to relate through such a function, and then proceed to learn it. This is accomplished by processing multiple simultaneous heterogeneous data streams (ensembles of time series) from observations of a physical system: multiple observation processes of the system. We thus determine (a) what subsets of observables are common between the observation processes (and therefore observable from each other, relatable through a function); and (b) what information is unrelated to these common observables, and therefore particular to each observation process, and not contributing to the desired function. Any data-driven function approximation technique can subsequently be used to learn the input-output relation, from k-nearest neighbors and Geometric Harmonics to Gaussian Processes and Neural Networks. Two particular ``twists'' of the approach are discussed. The first has to do with the identifiability of particular quantities of interest from the measurements. We now construct mappings from a single set of observations of one process to entire level sets of measurements of the process, consistent with this single set. The second attempts to relate our framework to a form of causality: if one of the observation processes measures ``now'', while the second observation process measures ``in the future'', the function to be learned among what is common across observation processes constitutes a dynamical model for the system evolution.

Machine Learning Enhanced Hankel Dynamic-Mode Decomposition

While the acquisition of time series has become increasingly more straightforward and sophisticated, developing dynamical models from time series is still a challenging and ever evolving problem domain. Within the last several years, to address this problem, there has been a merging of machine learning tools with what is called the dynamic mode decomposition (DMD). This general approach has been shown to be an especially promising avenue for sophisticated and accurate model development. Building on this prior body of work, we develop a deep learning DMD based method which makes use of the fundamental insight of Takens' Embedding Theorem to develop an adaptive learning scheme that better captures higher dimensional and chaotic dynamics. We call this method the Deep Learning Hankel DMD (DLHDMD). We show that the DLHDMD is able to generate accurate dynamics for chaotic time series, and we likewise explore how our method learns mappings which tend, after successful training, to significantly change the mutual information between dimensions in the dynamics. This appears to be a key feature in enhancing the DMD overall, and it should help provide further insight for developing more sophisticated deep learning methods for time series forecasting.

Next Generation Reservoir Computing

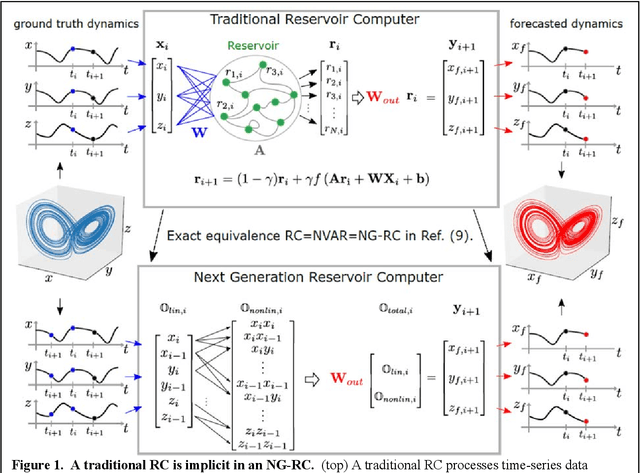
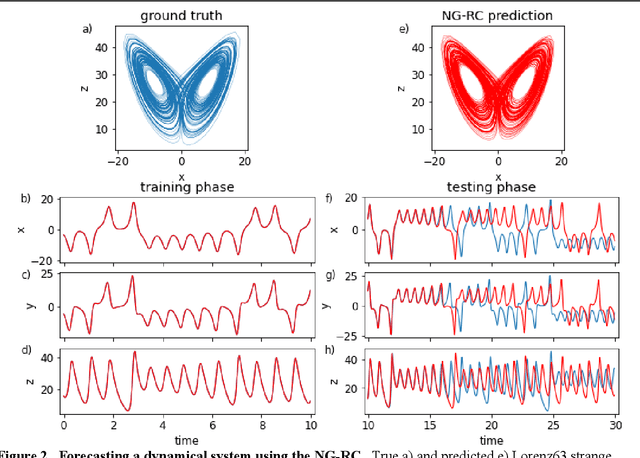
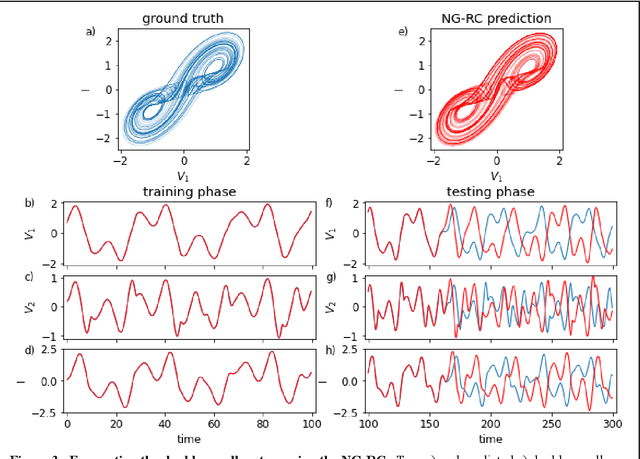
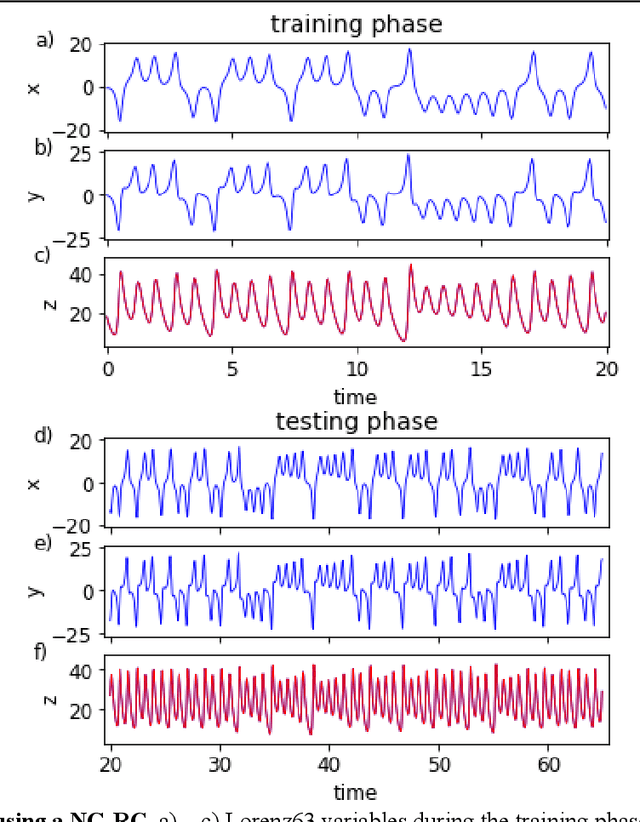
Reservoir computing is a best-in-class machine learning algorithm for processing information generated by dynamical systems using observed time-series data. Importantly, it requires very small training data sets, uses linear optimization, and thus requires minimal computing resources. However, the algorithm uses randomly sampled matrices to define the underlying recurrent neural network and has a multitude of metaparameters that must be optimized. Recent results demonstrate the equivalence of reservoir computing to nonlinear vector autoregression, which requires no random matrices, fewer metaparameters, and provides interpretable results. Here, we demonstrate that nonlinear vector autoregression excels at reservoir computing benchmark tasks and requires even shorter training data sets and training time, heralding the next generation of reservoir computing.

ERFit: Entropic Regression Fit Matlab Package, for Data-Driven System Identification of Underlying Dynamic Equations

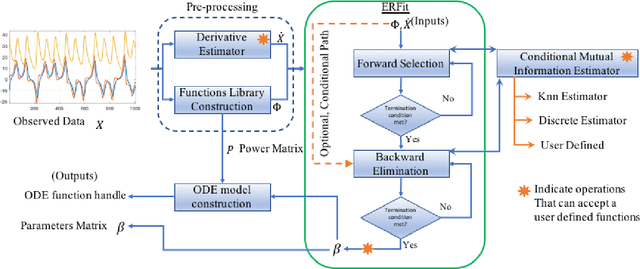
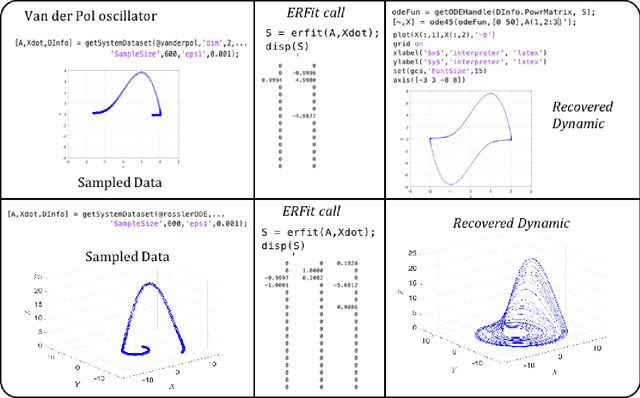
Data-driven sparse system identification becomes the general framework for a wide range of problems in science and engineering. It is a problem of growing importance in applied machine learning and artificial intelligence algorithms. In this work, we developed the Entropic Regression Software Package (ERFit), a MATLAB package for sparse system identification using the entropic regression method. The code requires minimal supervision, with a wide range of options that make it adapt easily to different problems in science and engineering. The ERFit is available at https://github.com/almomaa/ERFit-Package

Data-Driven Learning of Boolean Networks and Functions by Optimal Causation Entropy Principle

Boolean functions and networks are commonly used in the modeling and analysis of complex biological systems, and this paradigm is highly relevant in other important areas in data science and decision making, such as in the medical field and in the finance industry. Automated learning of a Boolean network and Boolean functions, from data, is a challenging task due in part to the large number of unknowns (including both the structure of the network and the functions) to be estimated, for which a brute force approach would be exponentially complex. In this paper we develop a new information theoretic methodology that we show to be significantly more efficient than previous approaches. Building on the recently developed optimal causation entropy principle (oCSE), that we proved can correctly infer networks distinguishing between direct versus indirect connections, we develop here an efficient algorithm that furthermore infers a Boolean network (including both its structure and function) based on data observed from the evolving states at nodes. We call this new inference method, Boolean optimal causation entropy (BoCSE), which we will show that our method is both computationally efficient and also resilient to noise. Furthermore, it allows for selection of a set of features that best explains the process, a statement that can be described as a networked Boolean function reduced order model. We highlight our method to the feature selection in several real-world examples: (1) diagnosis of urinary diseases, (2) Cardiac SPECT diagnosis, (3) informative positions in the game Tic-Tac-Toe, and (4) risk causality analysis of loans in default status. Our proposed method is effective and efficient in all examples.