Large Language Models for Constrained-Based Causal Discovery

Causality is essential for understanding complex systems, such as the economy, the brain, and the climate. Constructing causal graphs often relies on either data-driven or expert-driven approaches, both fraught with challenges. The former methods, like the celebrated PC algorithm, face issues with data requirements and assumptions of causal sufficiency, while the latter demand substantial time and domain knowledge. This work explores the capabilities of Large Language Models (LLMs) as an alternative to domain experts for causal graph generation. We frame conditional independence queries as prompts to LLMs and employ the PC algorithm with the answers. The performance of the LLM-based conditional independence oracle on systems with known causal graphs shows a high degree of variability. We improve the performance through a proposed statistical-inspired voting schema that allows some control over false-positive and false-negative rates. Inspecting the chain-of-thought argumentation, we find causal reasoning to justify its answer to a probabilistic query. We show evidence that knowledge-based CIT could eventually become a complementary tool for data-driven causal discovery.

Learning Staged Trees from Incomplete Data

Staged trees are probabilistic graphical models capable of representing any class of non-symmetric independence via a coloring of its vertices. Several structural learning routines have been defined and implemented to learn staged trees from data, under the frequentist or Bayesian paradigm. They assume a data set has been observed fully and, in practice, observations with missing entries are either dropped or imputed before learning the model. Here, we introduce the first algorithms for staged trees that handle missingness within the learning of the model. To this end, we characterize the likelihood of staged tree models in the presence of missing data and discuss pseudo-likelihoods that approximate it. A structural expectation-maximization algorithm estimating the model directly from the full likelihood is also implemented and evaluated. A computational experiment showcases the performance of the novel learning algorithms, demonstrating that it is feasible to account for different missingness patterns when learning staged trees.

Context-Specific Refinements of Bayesian Network Classifiers

Supervised classification is one of the most ubiquitous tasks in machine learning. Generative classifiers based on Bayesian networks are often used because of their interpretability and competitive accuracy. The widely used naive and TAN classifiers are specific instances of Bayesian network classifiers with a constrained underlying graph. This paper introduces novel classes of generative classifiers extending TAN and other famous types of Bayesian network classifiers. Our approach is based on staged tree models, which extend Bayesian networks by allowing for complex, context-specific patterns of dependence. We formally study the relationship between our novel classes of classifiers and Bayesian networks. We introduce and implement data-driven learning routines for our models and investigate their accuracy in an extensive computational study. The study demonstrates that models embedding asymmetric information can enhance classification accuracy.

Recovering Latent Confounders from High-dimensional Proxy Variables

Detecting latent confounders from proxy variables is an essential problem in causal effect estimation. Previous approaches are limited to low-dimensional proxies, sorted proxies, and binary treatments. We remove these assumptions and present a novel Proxy Confounder Factorization (PCF) framework for continuous treatment effect estimation when latent confounders manifest through high-dimensional, mixed proxy variables. For specific sample sizes, our two-step PCF implementation, using Independent Component Analysis (ICA-PCF), and the end-to-end implementation, using Gradient Descent (GD-PCF), achieve high correlation with the latent confounder and low absolute error in causal effect estimation with synthetic datasets in the high sample size regime. Even when faced with climate data, ICA-PCF recovers four components that explain $75.9\%$ of the variance in the North Atlantic Oscillation, a known confounder of precipitation patterns in Europe. Code for our PCF implementations and experiments can be found here: https://github.com/IPL-UV/confound_it. The proposed methodology constitutes a stepping stone towards discovering latent confounders and can be applied to many problems in disciplines dealing with high-dimensional observed proxies, e.g., spatiotemporal fields.

Improving generalisation via anchor multivariate analysis

We introduce a causal regularisation extension to anchor regression (AR) for improved out-of-distribution (OOD) generalisation. We present anchor-compatible losses, aligning with the anchor framework to ensure robustness against distribution shifts. Various multivariate analysis (MVA) algorithms, such as (Orthonormalized) PLS, RRR, and MLR, fall within the anchor framework. We observe that simple regularisation enhances robustness in OOD settings. Estimators for selected algorithms are provided, showcasing consistency and efficacy in synthetic and real-world climate science problems. The empirical validation highlights the versatility of anchor regularisation, emphasizing its compatibility with MVA approaches and its role in enhancing replicability while guarding against distribution shifts. The extended AR framework advances causal inference methodologies, addressing the need for reliable OOD generalisation.

Double machine learning for causal hybrid modeling -- applications in the Earth sciences

Hybrid modeling integrates machine learning with scientific knowledge with the goal of enhancing interpretability, generalization, and adherence to natural laws. Nevertheless, equifinality and regularization biases pose challenges in hybrid modeling to achieve these purposes. This paper introduces a novel approach to estimating hybrid models via a causal inference framework, specifically employing Double Machine Learning (DML) to estimate causal effects. We showcase its use for the Earth sciences on two problems related to carbon dioxide fluxes. In the $Q_{10}$ model, we demonstrate that DML-based hybrid modeling is superior in estimating causal parameters over end-to-end deep neural network (DNN) approaches, proving efficiency, robustness to bias from regularization methods, and circumventing equifinality. Our approach, applied to carbon flux partitioning, exhibits flexibility in accommodating heterogeneous causal effects. The study emphasizes the necessity of explicitly defining causal graphs and relationships, advocating for this as a general best practice. We encourage the continued exploration of causality in hybrid models for more interpretable and trustworthy results in knowledge-guided machine learning.

Discovering Causal Relations and Equations from Data

Physics is a field of science that has traditionally used the scientific method to answer questions about why natural phenomena occur and to make testable models that explain the phenomena. Discovering equations, laws and principles that are invariant, robust and causal explanations of the world has been fundamental in physical sciences throughout the centuries. Discoveries emerge from observing the world and, when possible, performing interventional studies in the system under study. With the advent of big data and the use of data-driven methods, causal and equation discovery fields have grown and made progress in computer science, physics, statistics, philosophy, and many applied fields. All these domains are intertwined and can be used to discover causal relations, physical laws, and equations from observational data. This paper reviews the concepts, methods, and relevant works on causal and equation discovery in the broad field of Physics and outlines the most important challenges and promising future lines of research. We also provide a taxonomy for observational causal and equation discovery, point out connections, and showcase a complete set of case studies in Earth and climate sciences, fluid dynamics and mechanics, and the neurosciences. This review demonstrates that discovering fundamental laws and causal relations by observing natural phenomena is being revolutionised with the efficient exploitation of observational data, modern machine learning algorithms and the interaction with domain knowledge. Exciting times are ahead with many challenges and opportunities to improve our understanding of complex systems.

Learning and interpreting asymmetry-labeled DAGs: a case study on COVID-19 fear

Bayesian networks are widely used to learn and reason about the dependence structure of discrete variables. However, they are only capable of formally encoding symmetric conditional independence, which in practice is often too strict to hold. Asymmetry-labeled DAGs have been recently proposed to both extend the class of Bayesian networks by relaxing the symmetric assumption of independence and denote the type of dependence existing between the variables of interest. Here, we introduce novel structural learning algorithms for this class of models which, whilst being efficient, allow for a straightforward interpretation of the underlying dependence structure. A comprehensive computational study highlights the efficiency of the algorithms. A real-world data application using data from the Fear of COVID-19 Scale collected in Italy showcases their use in practice.

Highly Efficient Structural Learning of Sparse Staged Trees

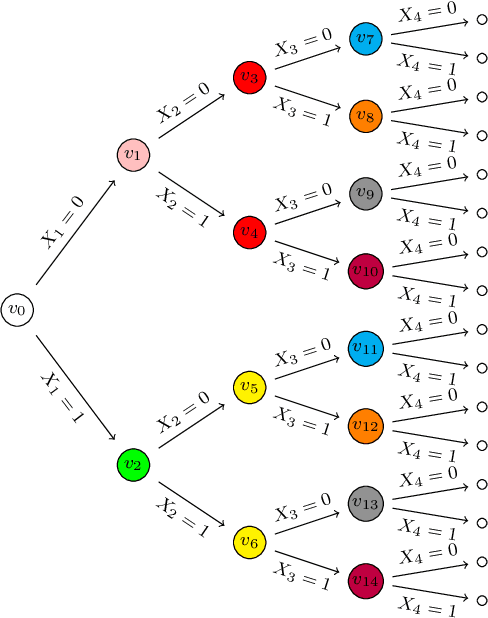
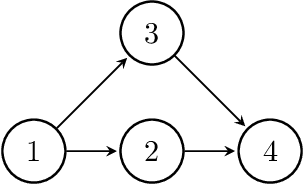
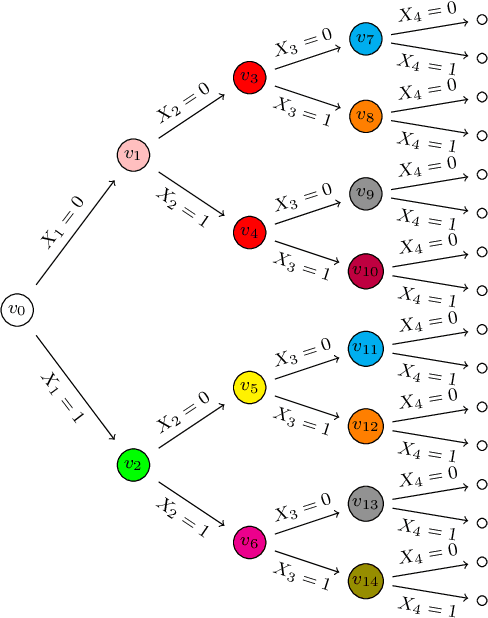
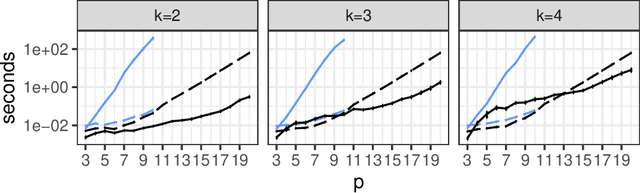
Several structural learning algorithms for staged tree models, an asymmetric extension of Bayesian networks, have been defined. However, they do not scale efficiently as the number of variables considered increases. Here we introduce the first scalable structural learning algorithm for staged trees, which searches over a space of models where only a small number of dependencies can be imposed. A simulation study as well as a real-world application illustrate our routines and the practical use of such data-learned staged trees.

Structural Learning of Simple Staged Trees

Bayesian networks faithfully represent the symmetric conditional independences existing between the components of a random vector. Staged trees are an extension of Bayesian networks for categorical random vectors whose graph represents non-symmetric conditional independences via vertex coloring. However, since they are based on a tree representation of the sample space, the underlying graph becomes cluttered and difficult to visualize as the number of variables increases. Here we introduce the first structural learning algorithms for the class of simple staged trees, entertaining a compact coalescence of the underlying tree from which non-symmetric independences can be easily read. We show that data-learned simple staged trees often outperform Bayesian networks in model fit and illustrate how the coalesced graph is used to identify non-symmetric conditional independences.