Trajectory Data Suffices for Statistically Efficient Learning in Offline RL with Linear $q^π$-Realizability and Concentrability

We consider offline reinforcement learning (RL) in $H$-horizon Markov decision processes (MDPs) under the linear $q^\pi$-realizability assumption, where the action-value function of every policy is linear with respect to a given $d$-dimensional feature function. The hope in this setting is that learning a good policy will be possible without requiring a sample size that scales with the number of states in the MDP. Foster et al. [2021] have shown this to be impossible even under $\textit{concentrability}$, a data coverage assumption where a coefficient $C_\text{conc}$ bounds the extent to which the state-action distribution of any policy can veer off the data distribution. However, the data in this previous work was in the form of a sequence of individual transitions. This leaves open the question of whether the negative result mentioned could be overcome if the data was composed of sequences of full trajectories. In this work we answer this question positively by proving that with trajectory data, a dataset of size $\text{poly}(d,H,C_\text{conc})/\epsilon^2$ is sufficient for deriving an $\epsilon$-optimal policy, regardless of the size of the state space. The main tool that makes this result possible is due to Weisz et al. [2023], who demonstrate that linear MDPs can be used to approximate linearly $q^\pi$-realizable MDPs. The connection to trajectory data is that the linear MDP approximation relies on "skipping" over certain states. The associated estimation problems are thus easy when working with trajectory data, while they remain nontrivial when working with individual transitions. The question of computational efficiency under our assumptions remains open.

Online RL in Linearly $q^π$-Realizable MDPs Is as Easy as in Linear MDPs If You Learn What to Ignore

We consider online reinforcement learning (RL) in episodic Markov decision processes (MDPs) under the linear $q^\pi$-realizability assumption, where it is assumed that the action-values of all policies can be expressed as linear functions of state-action features. This class is known to be more general than linear MDPs, where the transition kernel and the reward function are assumed to be linear functions of the feature vectors. As our first contribution, we show that the difference between the two classes is the presence of states in linearly $q^\pi$-realizable MDPs where for any policy, all the actions have approximately equal values, and skipping over these states by following an arbitrarily fixed policy in those states transforms the problem to a linear MDP. Based on this observation, we derive a novel (computationally inefficient) learning algorithm for linearly $q^\pi$-realizable MDPs that simultaneously learns what states should be skipped over and runs another learning algorithm on the linear MDP hidden in the problem. The method returns an $\epsilon$-optimal policy after $\text{polylog}(H, d)/\epsilon^2$ interactions with the MDP, where $H$ is the time horizon and $d$ is the dimension of the feature vectors, giving the first polynomial-sample-complexity online RL algorithm for this setting. The results are proved for the misspecified case, where the sample complexity is shown to degrade gracefully with the misspecification error.

Optimistic Natural Policy Gradient: a Simple Efficient Policy Optimization Framework for Online RL

While policy optimization algorithms have played an important role in recent empirical success of Reinforcement Learning (RL), the existing theoretical understanding of policy optimization remains rather limited -- they are either restricted to tabular MDPs or suffer from highly suboptimal sample complexity, especial in online RL where exploration is necessary. This paper proposes a simple efficient policy optimization framework -- Optimistic NPG for online RL. Optimistic NPG can be viewed as simply combining of the classic natural policy gradient (NPG) algorithm [Kakade, 2001] with optimistic policy evaluation subroutines to encourage exploration. For $d$-dimensional linear MDPs, Optimistic NPG is computationally efficient, and learns an $\varepsilon$-optimal policy within $\tilde{O}(d^2/\varepsilon^3)$ samples, which is the first computationally efficient algorithm whose sample complexity has the optimal dimension dependence $\tilde{\Theta}(d^2)$. It also improves over state-of-the-art results of policy optimization algorithms [Zanette et al., 2021] by a factor of $d$. For general function approximation that subsumes linear MDPs, Optimistic NPG, to our best knowledge, is also the first policy optimization algorithm that achieves the polynomial sample complexity for learning near-optimal policies.

Exponential Hardness of Reinforcement Learning with Linear Function Approximation

A fundamental question in reinforcement learning theory is: suppose the optimal value functions are linear in given features, can we learn them efficiently? This problem's counterpart in supervised learning, linear regression, can be solved both statistically and computationally efficiently. Therefore, it was quite surprising when a recent work \cite{kane2022computational} showed a computational-statistical gap for linear reinforcement learning: even though there are polynomial sample-complexity algorithms, unless NP = RP, there are no polynomial time algorithms for this setting. In this work, we build on their result to show a computational lower bound, which is exponential in feature dimension and horizon, for linear reinforcement learning under the Randomized Exponential Time Hypothesis. To prove this we build a round-based game where in each round the learner is searching for an unknown vector in a unit hypercube. The rewards in this game are chosen such that if the learner achieves large reward, then the learner's actions can be used to simulate solving a variant of 3-SAT, where (a) each variable shows up in a bounded number of clauses (b) if an instance has no solutions then it also has no solutions that satisfy more than (1-$\epsilon$)-fraction of clauses. We use standard reductions to show this 3-SAT variant is approximately as hard as 3-SAT. Finally, we also show a lower bound optimized for horizon dependence that almost matches the best known upper bound of $\exp(\sqrt{H})$.

Confident Approximate Policy Iteration for Efficient Local Planning in $q^π$-realizable MDPs

We consider approximate dynamic programming in $\gamma$-discounted Markov decision processes and apply it to approximate planning with linear value-function approximation. Our first contribution is a new variant of Approximate Policy Iteration (API), called Confident Approximate Policy Iteration (CAPI), which computes a deterministic stationary policy with an optimal error bound scaling linearly with the product of the effective horizon $H$ and the worst-case approximation error $\epsilon$ of the action-value functions of stationary policies. This improvement over API (whose error scales with $H^2$) comes at the price of an $H$-fold increase in memory cost. Unlike Scherrer and Lesner [2012], who recommended computing a non-stationary policy to achieve a similar improvement (with the same memory overhead), we are able to stick to stationary policies. This allows for our second contribution, the application of CAPI to planning with local access to a simulator and $d$-dimensional linear function approximation. As such, we design a planning algorithm that applies CAPI to obtain a sequence of policies with successively refined accuracies on a dynamically evolving set of states. The algorithm outputs an $\tilde O(\sqrt{d}H\epsilon)$-optimal policy after issuing $\tilde O(dH^4/\epsilon^2)$ queries to the simulator, simultaneously achieving the optimal accuracy bound and the best known query complexity bound, while earlier algorithms in the literature achieve only one of them. This query complexity is shown to be tight in all parameters except $H$. These improvements come at the expense of a mild (polynomial) increase in memory and computational costs of both the algorithm and its output policy.

TensorPlan and the Few Actions Lower Bound for Planning in MDPs under Linear Realizability of Optimal Value Functions

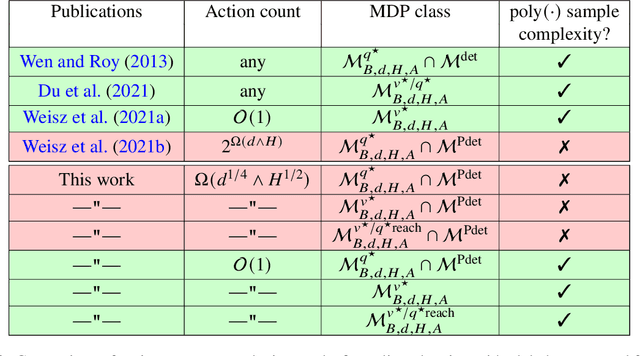
We consider the minimax query complexity of online planning with a generative model in fixed-horizon Markov decision processes (MDPs) with linear function approximation. Following recent works, we consider broad classes of problems where either (i) the optimal value function $v^\star$ or (ii) the optimal action-value function $q^\star$ lie in the linear span of some features; or (iii) both $v^\star$ and $q^\star$ lie in the linear span when restricted to the states reachable from the starting state. Recently, Weisz et al. (2021b) showed that under (ii) the minimax query complexity of any planning algorithm is at least exponential in the horizon $H$ or in the feature dimension $d$ when the size $A$ of the action set can be chosen to be exponential in $\min(d,H)$. On the other hand, for the setting (i), Weisz et al. (2021a) introduced TensorPlan, a planner whose query cost is polynomial in all relevant quantities when the number of actions is fixed. Among other things, these two works left open the question whether polynomial query complexity is possible when $A$ is subexponential in $min(d,H)$. In this paper we answer this question in the negative: we show that an exponentially large lower bound holds when $A=\Omega(\min(d^{1/4},H^{1/2}))$, under either (i), (ii) or (iii). In particular, this implies a perhaps surprising exponential separation of query complexity compared to the work of Du et al. (2021) who prove a polynomial upper bound when (iii) holds for all states. Furthermore, we show that the upper bound of TensorPlan can be extended to hold under (iii) and, for MDPs with deterministic transitions and stochastic rewards, also under (ii).

LeapsAndBounds: A Method for Approximately Optimal Algorithm Configuration

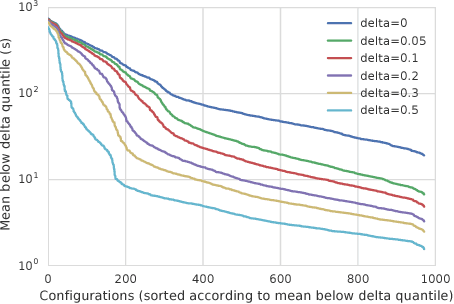
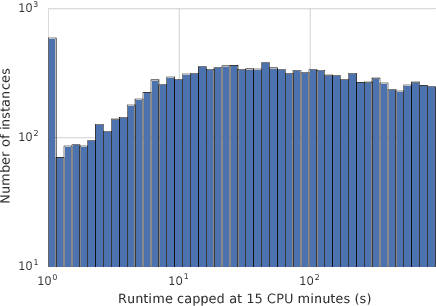
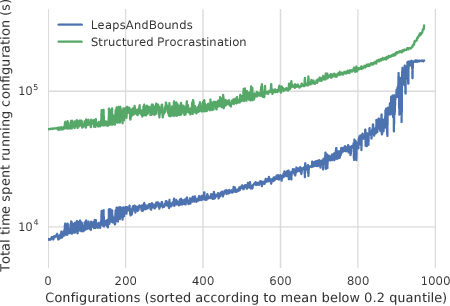
We consider the problem of configuring general-purpose solvers to run efficiently on problem instances drawn from an unknown distribution. The goal of the configurator is to find a configuration that runs fast on average on most instances, and do so with the least amount of total work. It can run a chosen solver on a random instance until the solver finishes or a timeout is reached. We propose LeapsAndBounds, an algorithm that tests configurations on randomly selected problem instances for longer and longer time. We prove that the capped expected runtime of the configuration returned by LeapsAndBounds is close to the optimal expected runtime, while our algorithm's running time is near-optimal. Our results show that LeapsAndBounds is more efficient than the recent algorithm of Kleinberg et al. (2017), which, to our knowledge, is the only other algorithm configuration method with non-trivial theoretical guarantees. Experimental results on configuring a public SAT solver on a new benchmark dataset also stand witness to the superiority of our method.

Sample Efficient Deep Reinforcement Learning for Dialogue Systems with Large Action Spaces

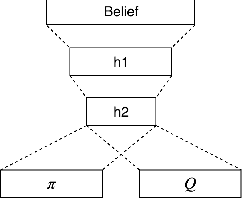
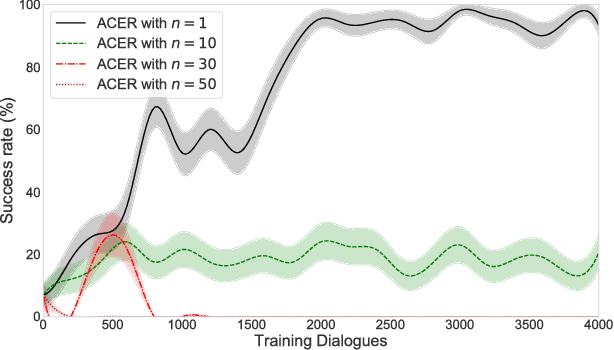
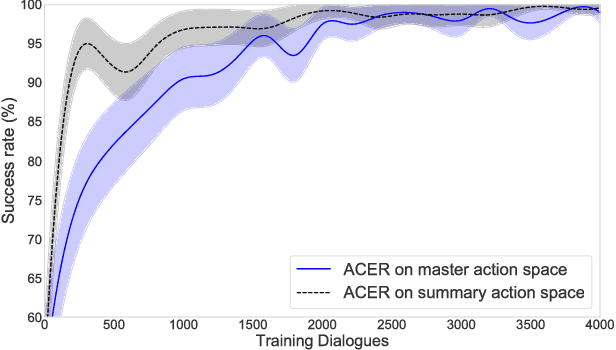
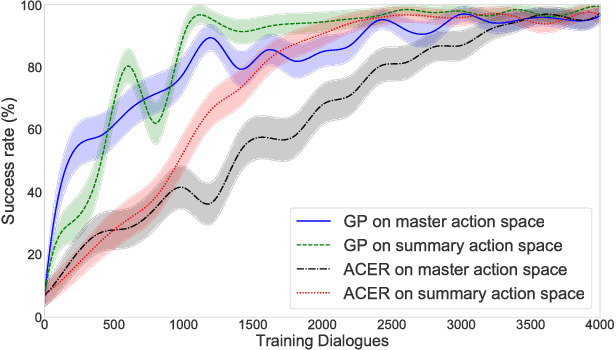
In spoken dialogue systems, we aim to deploy artificial intelligence to build automated dialogue agents that can converse with humans. A part of this effort is the policy optimisation task, which attempts to find a policy describing how to respond to humans, in the form of a function taking the current state of the dialogue and returning the response of the system. In this paper, we investigate deep reinforcement learning approaches to solve this problem. Particular attention is given to actor-critic methods, off-policy reinforcement learning with experience replay, and various methods aimed at reducing the bias and variance of estimators. When combined, these methods result in the previously proposed ACER algorithm that gave competitive results in gaming environments. These environments however are fully observable and have a relatively small action set so in this paper we examine the application of ACER to dialogue policy optimisation. We show that this method beats the current state-of-the-art in deep learning approaches for spoken dialogue systems. This not only leads to a more sample efficient algorithm that can train faster, but also allows us to apply the algorithm in more difficult environments than before. We thus experiment with learning in a very large action space, which has two orders of magnitude more actions than previously considered. We find that ACER trains significantly faster than the current state-of-the-art.