Non-PSD Matrix Sketching with Applications to Regression and Optimization

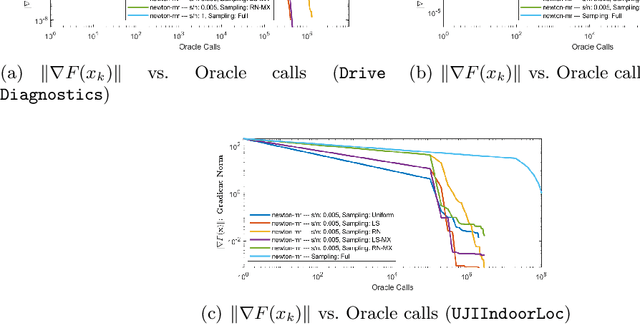
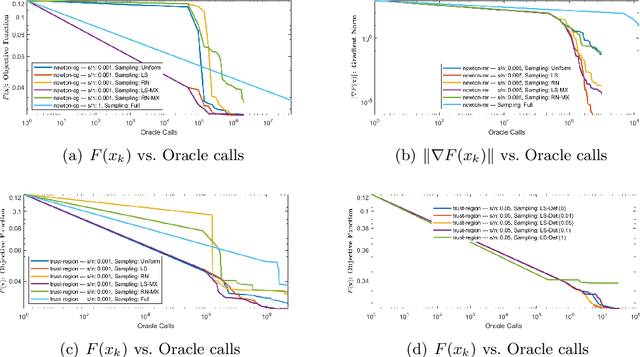
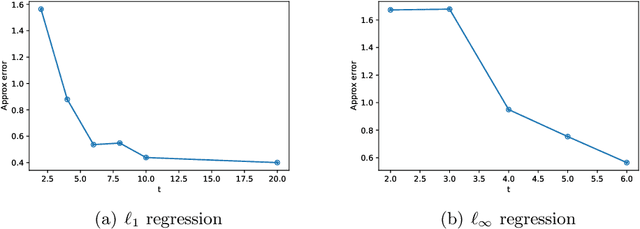
A variety of dimensionality reduction techniques have been applied for computations involving large matrices. The underlying matrix is randomly compressed into a smaller one, while approximately retaining many of its original properties. As a result, much of the expensive computation can be performed on the small matrix. The sketching of positive semidefinite (PSD) matrices is well understood, but there are many applications where the related matrices are not PSD, including Hessian matrices in non-convex optimization and covariance matrices in regression applications involving complex numbers. In this paper, we present novel dimensionality reduction methods for non-PSD matrices, as well as their ``square-roots", which involve matrices with complex entries. We show how these techniques can be used for multiple downstream tasks. In particular, we show how to use the proposed matrix sketching techniques for both convex and non-convex optimization, $\ell_p$-regression for every $1 \leq p \leq \infty$, and vector-matrix-vector queries.

Average-reward model-free reinforcement learning: a systematic review and literature mapping

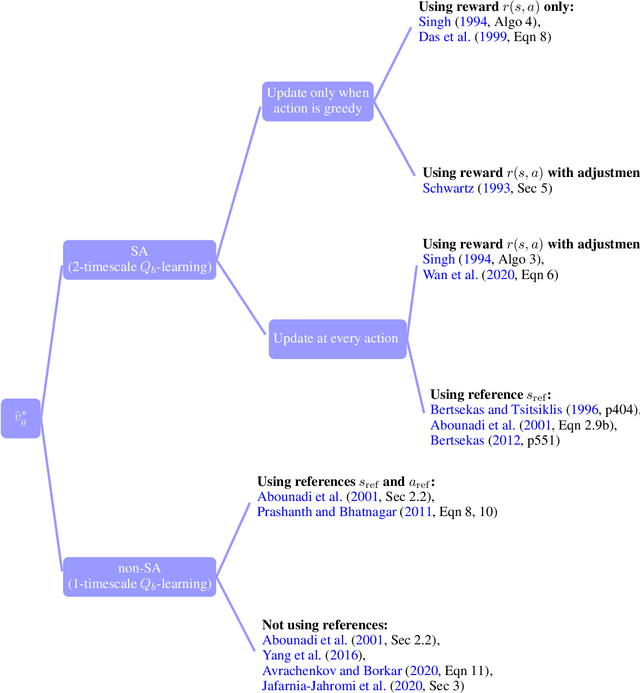
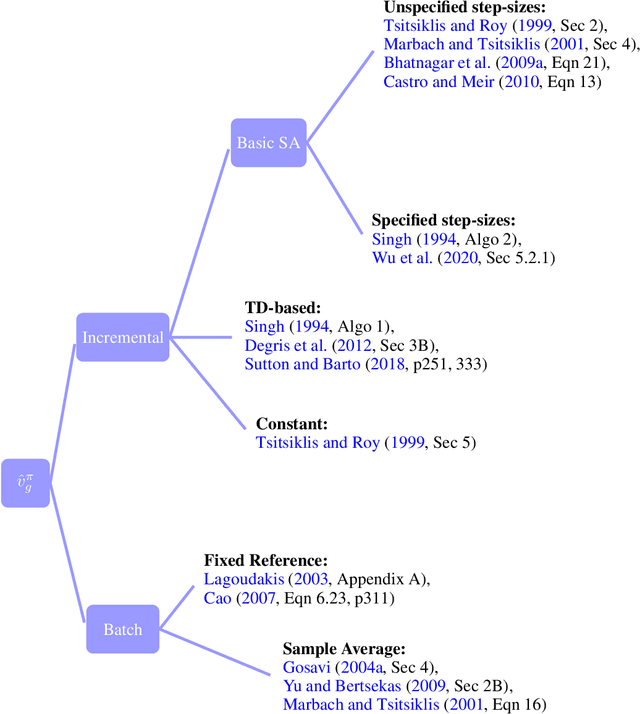
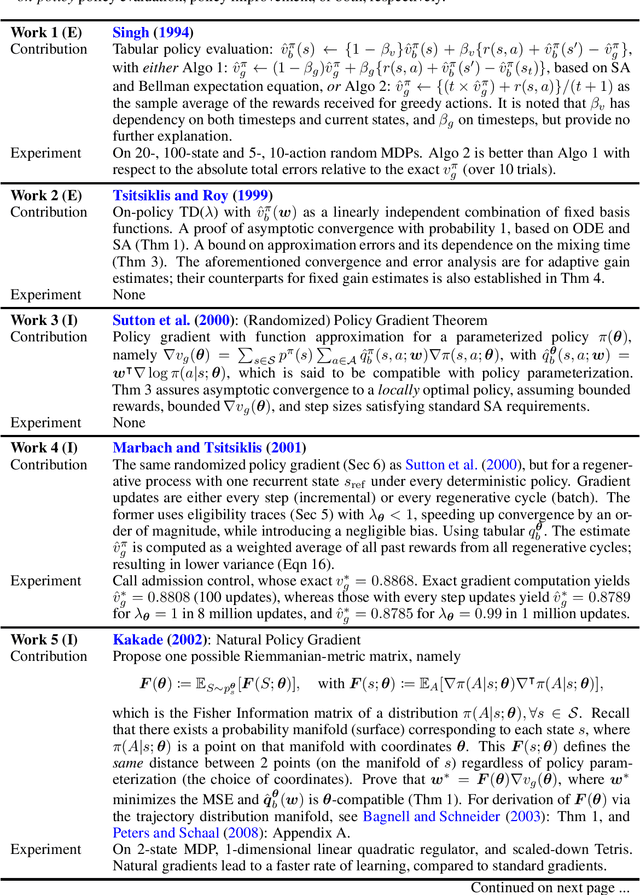
Model-free reinforcement learning (RL) has been an active area of research and provides a fundamental framework for agent-based learning and decision-making in artificial intelligence. In this paper, we review a specific subset of this literature, namely work that utilizes optimization criteria based on average rewards, in the infinite horizon setting. Average reward RL has the advantage of being the most selective criterion in recurrent (ergodic) Markov decision processes. In comparison to widely-used discounted reward criterion, it also requires no discount factor, which is a critical hyperparameter, and properly aligns the optimization and performance metrics. Motivated by the solo survey by Mahadevan (1996a), we provide an updated review of work in this area and extend it to cover policy-iteration and function approximation methods (in addition to the value-iteration and tabular counterparts). We also identify and discuss opportunities for future work.

Stochastic Normalizing Flows

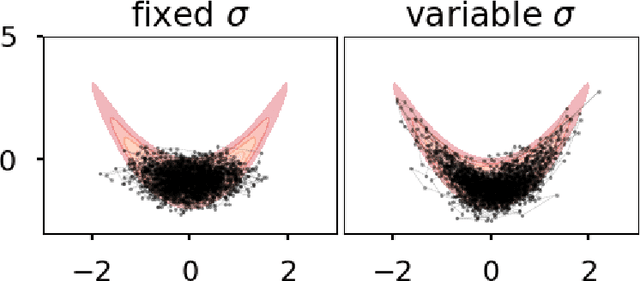
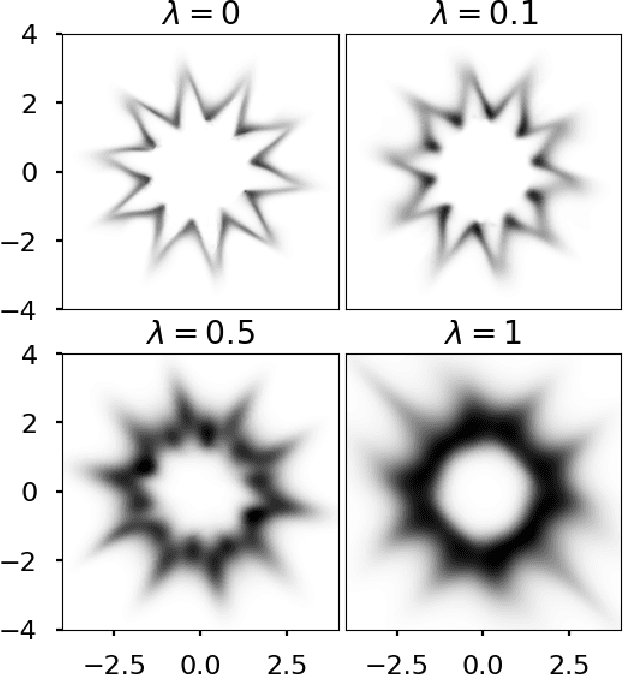
We introduce stochastic normalizing flows, an extension of continuous normalizing flows for maximum likelihood estimation and variational inference (VI) using stochastic differential equations (SDEs). Using the theory of rough paths, the underlying Brownian motion is treated as a latent variable and approximated, enabling efficient training of neural SDEs as random neural ordinary differential equations. These SDEs can be used for constructing efficient Markov chains to sample from the underlying distribution of a given dataset. Furthermore, by considering families of targeted SDEs with prescribed stationary distribution, we can apply VI to the optimization of hyperparameters in stochastic MCMC.

Avoiding Kernel Fixed Points: Computing with ELU and GELU Infinite Networks

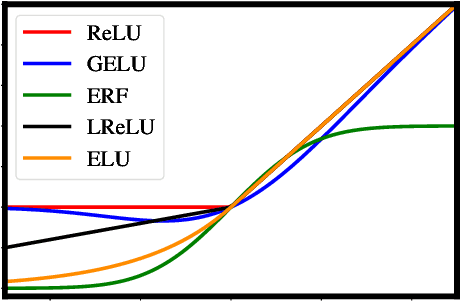
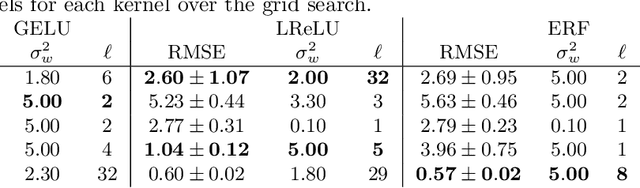
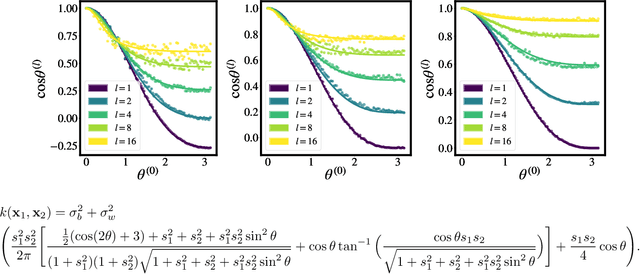
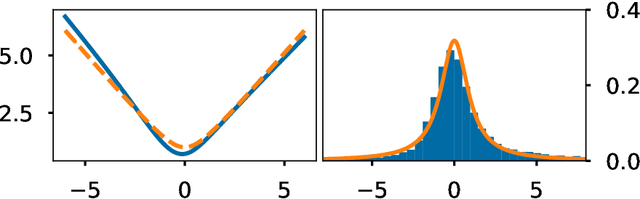
Analysing and computing with Gaussian processes arising from infinitely wide neural networks has recently seen a resurgence in popularity. Despite this, many explicit covariance functions of networks with activation functions used in modern networks remain unknown. Furthermore, while the kernels of deep networks can be computed iteratively, theoretical understanding of deep kernels is lacking, particularly with respect to fixed-point dynamics. Firstly, we derive the covariance functions of MLPs with exponential linear units and Gaussian error linear units and evaluate the performance of the limiting Gaussian processes on some benchmarks. Secondly, and more generally, we introduce a framework for analysing the fixed-point dynamics of iterated kernels corresponding to a broad range of activation functions. We find that unlike some previously studied neural network kernels, these new kernels exhibit non-trivial fixed-point dynamics which are mirrored in finite-width neural networks.

The reproducing Stein kernel approach for post-hoc corrected sampling

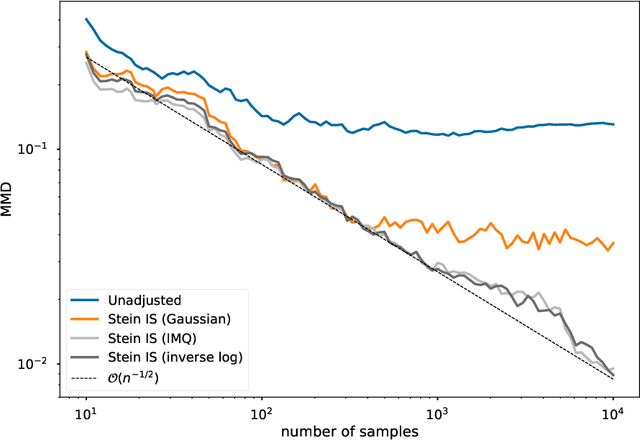
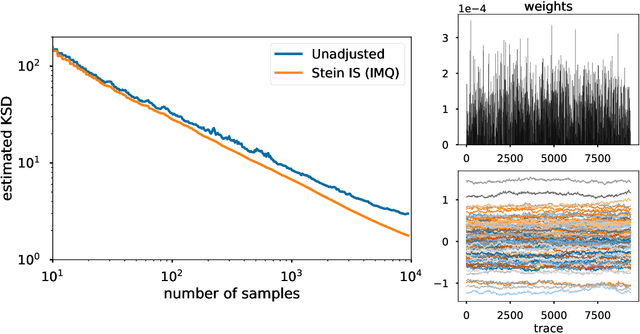
Stein importance sampling is a widely applicable technique based on kernelized Stein discrepancy, which corrects the output of approximate sampling algorithms by reweighting the empirical distribution of the samples. A general analysis of this technique is conducted for the previously unconsidered setting where samples are obtained via the simulation of a Markov chain, and applies to an arbitrary underlying Polish space. We prove that Stein importance sampling yields consistent estimators for quantities related to a target distribution of interest by using samples obtained from a geometrically ergodic Markov chain with a possibly unknown invariant measure that differs from the desired target. The approach is shown to be valid under conditions that are satisfied for a large number of unadjusted samplers, and is capable of retaining consistency when data subsampling is used. Along the way, a universal theory of reproducing Stein kernels is established, which enables the construction of kernelized Stein discrepancy on general Polish spaces, and provides sufficient conditions for kernels to be convergence-determining on such spaces. These results are of independent interest for the development of future methodology based on kernelized Stein discrepancies.

LSAR: Efficient Leverage Score Sampling Algorithm for the Analysis of Big Time Series Data

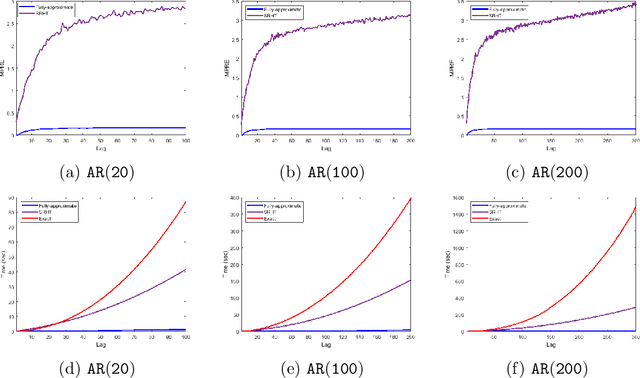
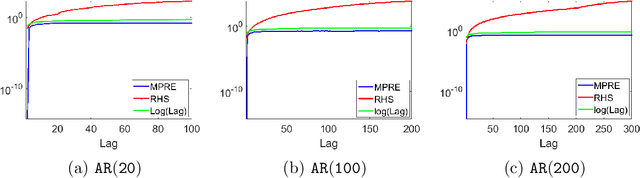
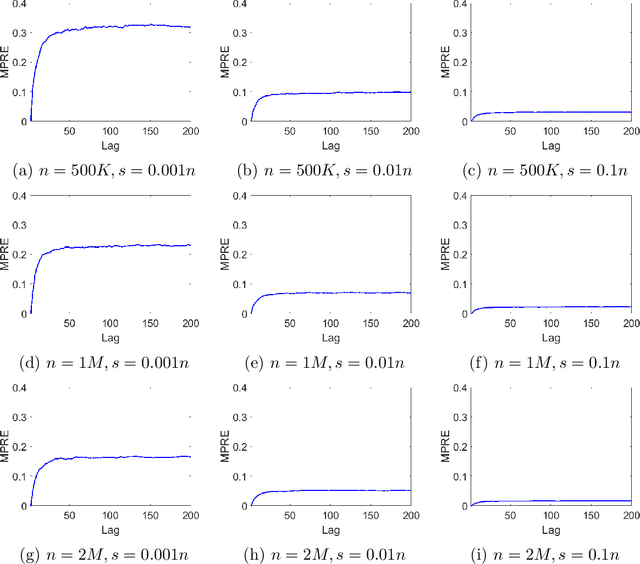
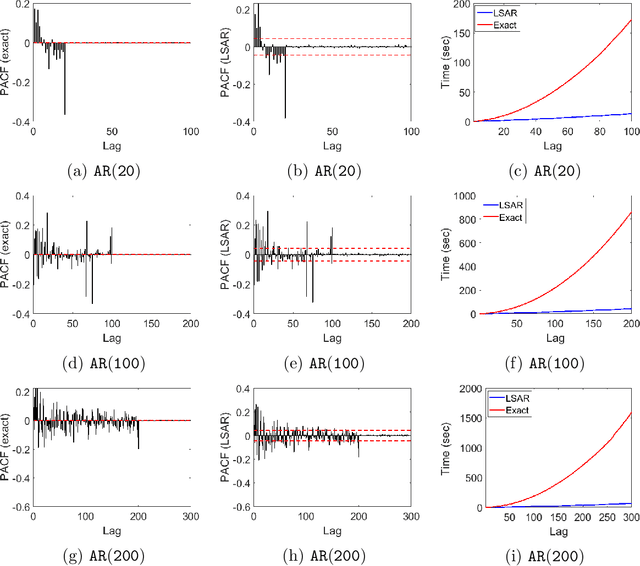
We apply methods from randomized numerical linear algebra (RandNLA) to develop improved algorithms for the analysis of large-scale time series data. We first develop a new fast algorithm to estimate the leverage scores of an autoregressive (AR) model in big data regimes. We show that the accuracy of approximations lies within $(1+\mathcal{O}(\varepsilon))$ of the true leverage scores with high probability. These theoretical results are subsequently exploited to develop an efficient algorithm, called LSAR, for fitting an appropriate AR model to big time series data. Our proposed algorithm is guaranteed, with high probability, to find the maximum likelihood estimates of the parameters of the underlying true AR model and has a worst case running time that significantly improves those of the state-of-the-art alternatives in big data regimes. Empirical results on large-scale synthetic as well as real data highly support the theoretical results and reveal the efficacy of this new approach.

Richer priors for infinitely wide multi-layer perceptrons

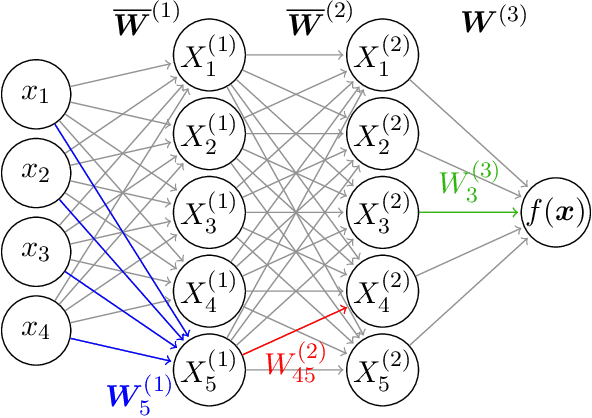
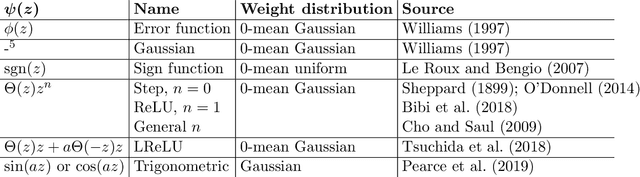
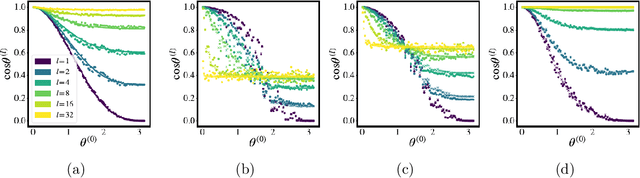
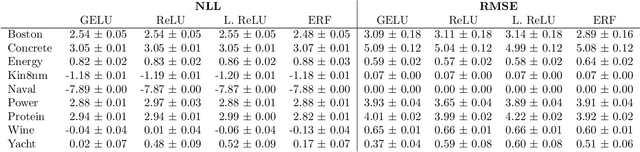
It is well-known that the distribution over functions induced through a zero-mean iid prior distribution over the parameters of a multi-layer perceptron (MLP) converges to a Gaussian process (GP), under mild conditions. We extend this result firstly to independent priors with general zero or non-zero means, and secondly to a family of partially exchangeable priors which generalise iid priors. We discuss how the second prior arises naturally when considering an equivalence class of functions in an MLP and through training processes such as stochastic gradient descent. The model resulting from partially exchangeable priors is a GP, with an additional level of inference in the sense that the prior and posterior predictive distributions require marginalisation over hyperparameters. We derive the kernels of the limiting GP in deep MLPs, and show empirically that these kernels avoid certain pathologies present in previously studied priors. We empirically evaluate our claims of convergence by measuring the maximum mean discrepancy between finite width models and limiting models. We compare the performance of our new limiting model to some previously discussed models on synthetic regression problems. We observe increasing ill-conditioning of the marginal likelihood and hyper-posterior as the depth of the model increases, drawing parallels with finite width networks which require notoriously involved optimisation tricks.

Limit theorems for out-of-sample extensions of the adjacency and Laplacian spectral embeddings

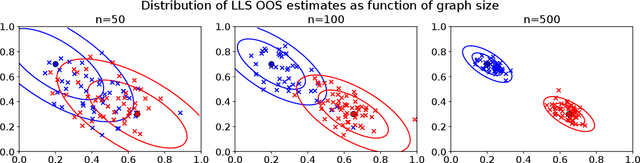
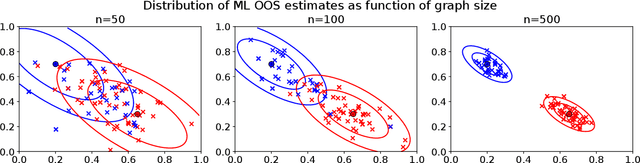
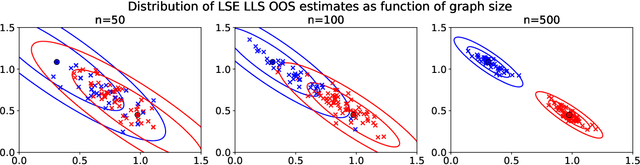
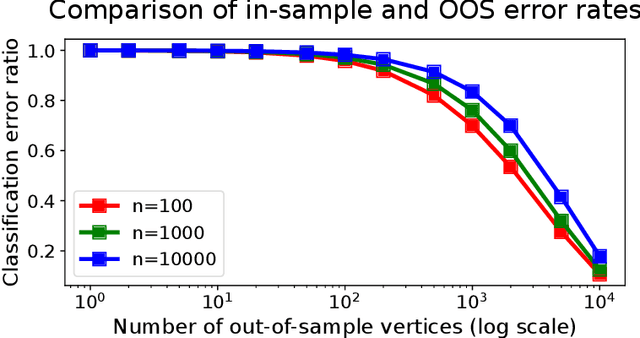
Graph embeddings, a class of dimensionality reduction techniques designed for relational data, have proven useful in exploring and modeling network structure. Most dimensionality reduction methods allow out-of-sample extensions, by which an embedding can be applied to observations not present in the training set. Applied to graphs, the out-of-sample extension problem concerns how to compute the embedding of a vertex that is added to the graph after an embedding has already been computed. In this paper, we consider the out-of-sample extension problem for two graph embedding procedures: the adjacency spectral embedding and the Laplacian spectral embedding. In both cases, we prove that when the underlying graph is generated according to a latent space model called the random dot product graph, which includes the popular stochastic block model as a special case, an out-of-sample extension based on a least-squares objective obeys a central limit theorem about the true latent position of the out-of-sample vertex. In addition, we prove a concentration inequality for the out-of-sample extension of the adjacency spectral embedding based on a maximum-likelihood objective. Our results also yield a convenient framework in which to analyze trade-offs between estimation accuracy and computational expense, which we explore briefly.

Implicit Langevin Algorithms for Sampling From Log-concave Densities

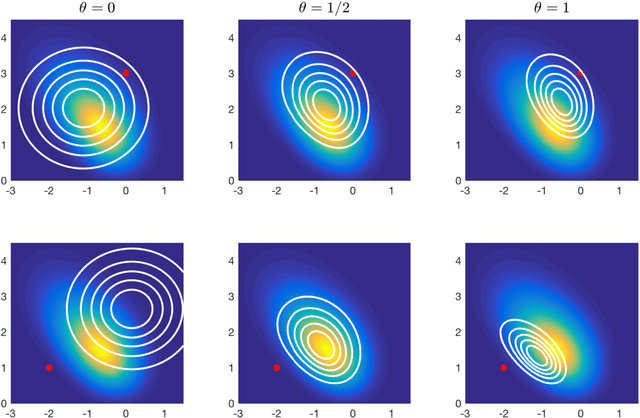
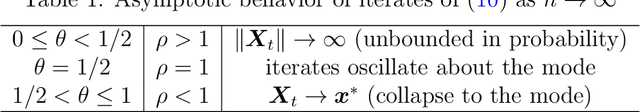
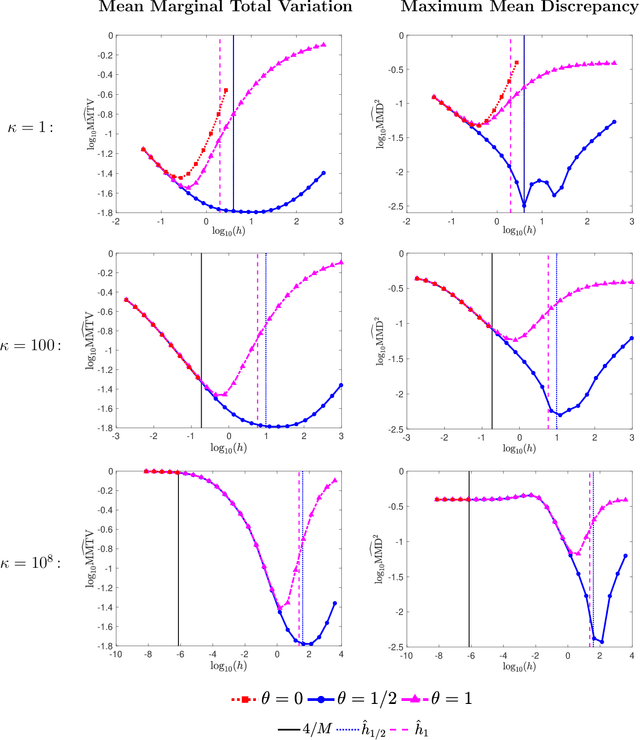
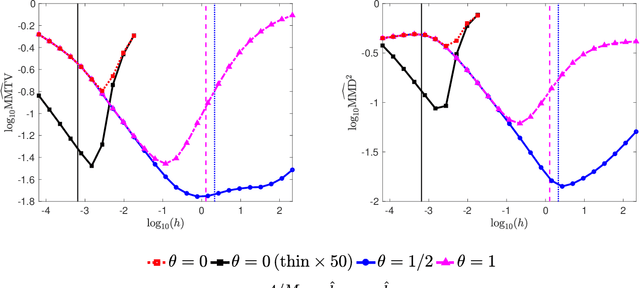
For sampling from a log-concave density, we study implicit integrators resulting from $\theta$-method discretization of the overdamped Langevin diffusion stochastic differential equation. Theoretical and algorithmic properties of the resulting sampling methods for $ \theta \in [0,1] $ and a range of step sizes are established. Our results generalize and extend prior works in several directions. In particular, for $\theta\ge1/2$, we prove geometric ergodicity and stability of the resulting methods for all step sizes. We show that obtaining subsequent samples amounts to solving a strongly-convex optimization problem, which is readily achievable using one of numerous existing methods. Numerical examples supporting our theoretical analysis are also presented.

DINGO: Distributed Newton-Type Method for Gradient-Norm Optimization

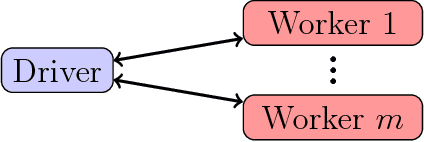
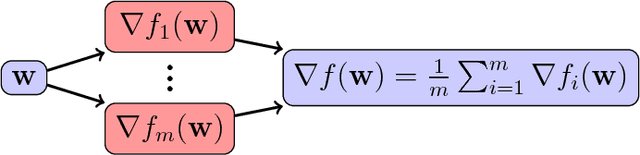
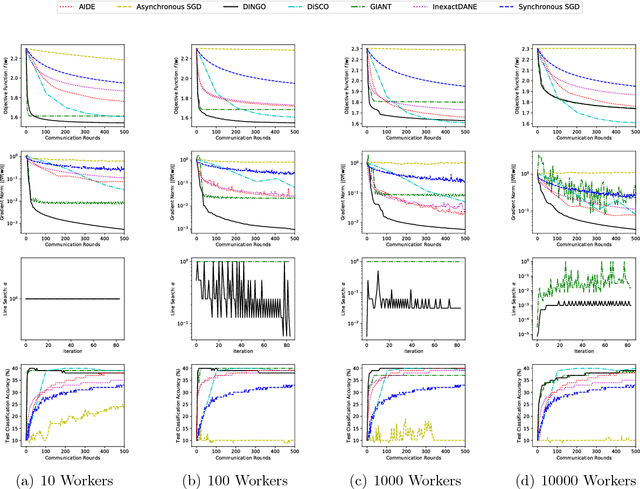
For optimization of a sum of functions in a distributed computing environment, we present a novel communication efficient Newton-type algorithm that enjoys a variety of advantages over similar existing methods. Similar to Newton-MR, our algorithm, DINGO, is derived by optimization of the gradient's norm as a surrogate function. DINGO does not impose any specific form on the underlying functions, and its application range extends far beyond convexity. In addition, the distribution of the data across the computing environment can be almost arbitrary. Further, the underlying sub-problems of DINGO are simple linear least-squares, for which a plethora of efficient algorithms exist. Lastly, DINGO involves a few hyper-parameters that are easy to tune. Moreover, we theoretically show that DINGO is not sensitive to the choice of its hyper-parameters in that a strict reduction in the gradient norm is guaranteed, regardless of the selected hyper-parameters. We demonstrate empirical evidence of the effectiveness, stability and versatility of our method compared to other relevant algorithms, on both convex and non-convex problems.