Tensor Frames -- How To Make Any Message Passing Network Equivariant

In many applications of geometric deep learning, the choice of global coordinate frame is arbitrary, and predictions should be independent of the reference frame. In other words, the network should be equivariant with respect to rotations and reflections of the input, i.e., the transformations of O(d). We present a novel framework for building equivariant message passing architectures and modifying existing non-equivariant architectures to be equivariant. Our approach is based on local coordinate frames, between which geometric information is communicated consistently by including tensorial objects in the messages. Our framework can be applied to message passing on geometric data in arbitrary dimensional Euclidean space. While many other approaches for equivariant message passing require specialized building blocks, such as non-standard normalization layers or non-linearities, our approach can be adapted straightforwardly to any existing architecture without such modifications. We explicitly demonstrate the benefit of O(3)-equivariance for a popular point cloud architecture and produce state-of-the-art results on normal vector regression on point clouds.

SynCellFactory: Generative Data Augmentation for Cell Tracking

Cell tracking remains a pivotal yet challenging task in biomedical research. The full potential of deep learning for this purpose is often untapped due to the limited availability of comprehensive and varied training data sets. In this paper, we present SynCellFactory, a generative cell video augmentation. At the heart of SynCellFactory lies the ControlNet architecture, which has been fine-tuned to synthesize cell imagery with photorealistic accuracy in style and motion patterns. This technique enables the creation of synthetic yet realistic cell videos that mirror the complexity of authentic microscopy time-lapses. Our experiments demonstrate that SynCellFactory boosts the performance of well-established deep learning models for cell tracking, particularly when original training data is sparse.

The Central Spanning Tree Problem

Spanning trees are an important primitive in many data analysis tasks, when a data set needs to be summarized in terms of its "skeleton", or when a tree-shaped graph over all observations is required for downstream processing. Popular definitions of spanning trees include the minimum spanning tree and the optimum distance spanning tree, a.k.a. the minimum routing cost tree. When searching for the shortest spanning tree but admitting additional branching points, even shorter spanning trees can be realized: Steiner trees. Unfortunately, both minimum spanning and Steiner trees are not robust with respect to noise in the observations; that is, small perturbations of the original data set often lead to drastic changes in the associated spanning trees. In response, we make two contributions when the data lies in a Euclidean space: on the theoretical side, we introduce a new optimization problem, the "(branched) central spanning tree", which subsumes all previously mentioned definitions as special cases. On the practical side, we show empirically that the (branched) central spanning tree is more robust to noise in the data, and as such is better suited to summarize a data set in terms of its skeleton. We also propose a heuristic to address the NP-hard optimization problem, and illustrate its use on single cell RNA expression data from biology and 3D point clouds of plants.

Geometric Autoencoders -- What You See is What You Decode

Visualization is a crucial step in exploratory data analysis. One possible approach is to train an autoencoder with low-dimensional latent space. Large network depth and width can help unfolding the data. However, such expressive networks can achieve low reconstruction error even when the latent representation is distorted. To avoid such misleading visualizations, we propose first a differential geometric perspective on the decoder, leading to insightful diagnostics for an embedding's distortion, and second a new regularizer mitigating such distortion. Our ``Geometric Autoencoder'' avoids stretching the embedding spuriously, so that the visualization captures the data structure more faithfully. It also flags areas where little distortion could not be achieved, thus guarding against misinterpretation.

KineticNet: Deep learning a transferable kinetic energy functional for orbital-free density functional theory

Orbital-free density functional theory (OF-DFT) holds the promise to compute ground state molecular properties at minimal cost. However, it has been held back by our inability to compute the kinetic energy as a functional of the electron density only. We here set out to learn the kinetic energy functional from ground truth provided by the more expensive Kohn-Sham density functional theory. Such learning is confronted with two key challenges: Giving the model sufficient expressivity and spatial context while limiting the memory footprint to afford computations on a GPU; and creating a sufficiently broad distribution of training data to enable iterative density optimization even when starting from a poor initial guess. In response, we introduce KineticNet, an equivariant deep neural network architecture based on point convolutions adapted to the prediction of quantities on molecular quadrature grids. Important contributions include convolution filters with sufficient spatial resolution in the vicinity of the nuclear cusp, an atom-centric sparse but expressive architecture that relays information across multiple bond lengths; and a new strategy to generate varied training data by finding ground state densities in the face of perturbations by a random external potential. KineticNet achieves, for the first time, chemical accuracy of the learned functionals across input densities and geometries of tiny molecules. For two electron systems, we additionally demonstrate OF-DFT density optimization with chemical accuracy.

Theory and Approximate Solvers for Branched Optimal Transport with Multiple Sources

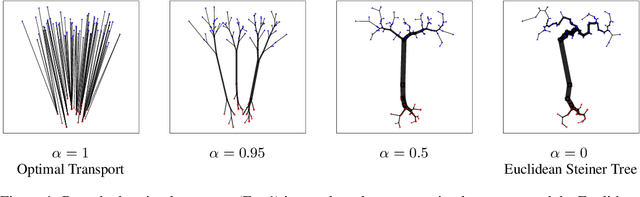
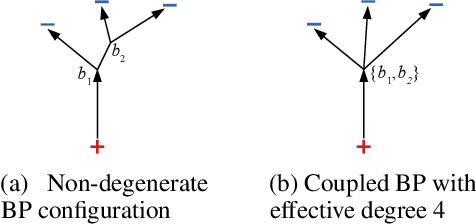
Branched Optimal Transport (BOT) is a generalization of optimal transport in which transportation costs along an edge are subadditive. This subadditivity models an increase in transport efficiency when shipping mass along the same route, favoring branched transportation networks. We here study the NP-hard optimization of BOT networks connecting a finite number of sources and sinks in $\mathbb{R}^2$. First, we show how to efficiently find the best geometry of a BOT network for many sources and sinks, given a topology. Second, we argue that a topology with more than three edges meeting at a branching point is never optimal. Third, we show that the results obtained for the Euclidean plane generalize directly to optimal transportation networks on two-dimensional Riemannian manifolds. Finally, we present a simple but effective approximate BOT solver combining geometric optimization with a combinatorial optimization of the network topology.

Contrastive learning unifies $t$-SNE and UMAP

Neighbor embedding methods $t$-SNE and UMAP are the de facto standard for visualizing high-dimensional datasets. They appear to use very different loss functions with different motivations, and the exact relationship between them has been unclear. Here we show that UMAP is effectively negative sampling applied to the $t$-SNE loss function. We explain the difference between negative sampling and noise-contrastive estimation (NCE), which has been used to optimize $t$-SNE under the name NCVis. We prove that, unlike NCE, negative sampling learns a scaled data distribution. When applied in the neighbor embedding setting, it yields more compact embeddings with increased attraction, explaining differences in appearance between UMAP and $t$-SNE. Further, we generalize the notion of negative sampling and obtain a spectrum of embeddings, encompassing visualizations similar to $t$-SNE, NCVis, and UMAP. Finally, we explore the connection between representation learning in the SimCLR setting and neighbor embeddings, and show that (i) $t$-SNE can be optimized using the InfoNCE loss and in a parametric setting; (ii) various contrastive losses with only few noise samples can yield competitive performance in the SimCLR setup.

CellTypeGraph: A New Geometric Computer Vision Benchmark

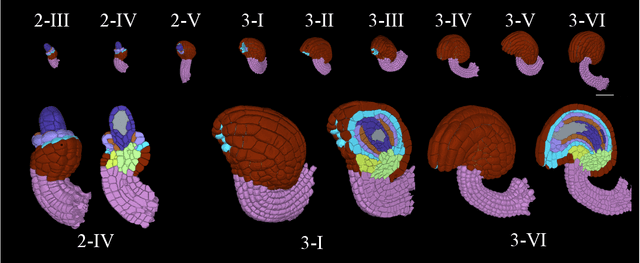
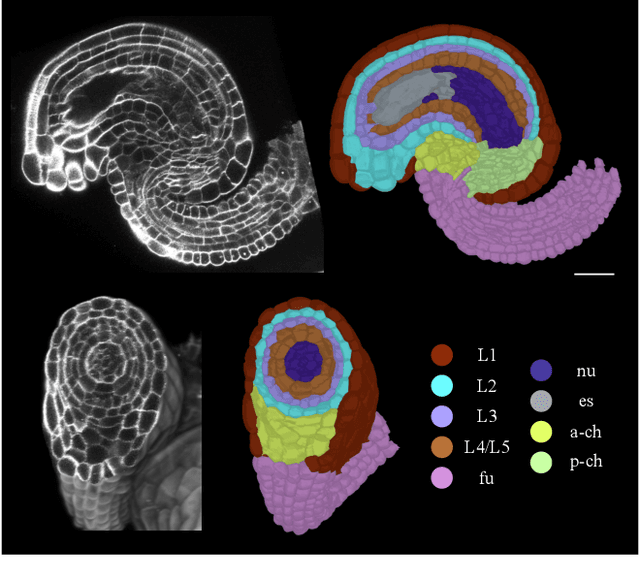
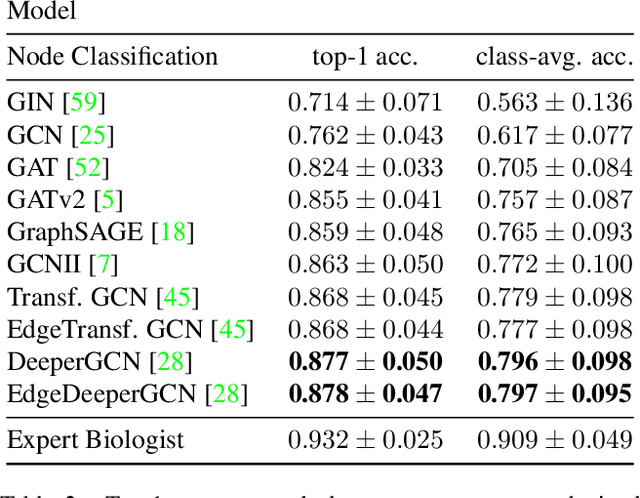
Classifying all cells in an organ is a relevant and difficult problem from plant developmental biology. We here abstract the problem into a new benchmark for node classification in a geo-referenced graph. Solving it requires learning the spatial layout of the organ including symmetries. To allow the convenient testing of new geometrical learning methods, the benchmark of Arabidopsis thaliana ovules is made available as a PyTorch data loader, along with a large number of precomputed features. Finally, we benchmark eight recent graph neural network architectures, finding that DeeperGCN currently works best on this problem.

Extensions of Karger's Algorithm: Why They Fail in Theory and How They Are Useful in Practice

The minimum graph cut and minimum $s$-$t$-cut problems are important primitives in the modeling of combinatorial problems in computer science, including in computer vision and machine learning. Some of the most efficient algorithms for finding global minimum cuts are randomized algorithms based on Karger's groundbreaking contraction algorithm. Here, we study whether Karger's algorithm can be successfully generalized to other cut problems. We first prove that a wide class of natural generalizations of Karger's algorithm cannot efficiently solve the $s$-$t$-mincut or the normalized cut problem to optimality. However, we then present a simple new algorithm for seeded segmentation / graph-based semi-supervised learning that is closely based on Karger's original algorithm, showing that for these problems, extensions of Karger's algorithm can be useful. The new algorithm has linear asymptotic runtime and yields a potential that can be interpreted as the posterior probability of a sample belonging to a given seed / class. We clarify its relation to the random walker algorithm / harmonic energy minimization in terms of distributions over spanning forests. On classical problems from seeded image segmentation and graph-based semi-supervised learning on image data, the method performs at least as well as the random walker / harmonic energy minimization / Gaussian processes.

On UMAP's true loss function

UMAP has supplanted t-SNE as state-of-the-art for visualizing high-dimensional datasets in many disciplines, but the reason for its success is not well understood. In this work, we investigate UMAP's sampling based optimization scheme in detail. We derive UMAP's effective loss function in closed form and find that it differs from the published one. As a consequence, we show that UMAP does not aim to reproduce its theoretically motivated high-dimensional UMAP similarities. Instead, it tries to reproduce similarities that only encode the shared $k$ nearest neighbor graph, thereby challenging the previous understanding of UMAP's effectiveness. Instead, we claim that the key to UMAP's success is its implicit balancing of attraction and repulsion resulting from negative sampling. This balancing in turn facilitates optimization via gradient descent. We corroborate our theoretical findings on toy and single cell RNA sequencing data.