Tensor Frames -- How To Make Any Message Passing Network Equivariant

In many applications of geometric deep learning, the choice of global coordinate frame is arbitrary, and predictions should be independent of the reference frame. In other words, the network should be equivariant with respect to rotations and reflections of the input, i.e., the transformations of O(d). We present a novel framework for building equivariant message passing architectures and modifying existing non-equivariant architectures to be equivariant. Our approach is based on local coordinate frames, between which geometric information is communicated consistently by including tensorial objects in the messages. Our framework can be applied to message passing on geometric data in arbitrary dimensional Euclidean space. While many other approaches for equivariant message passing require specialized building blocks, such as non-standard normalization layers or non-linearities, our approach can be adapted straightforwardly to any existing architecture without such modifications. We explicitly demonstrate the benefit of O(3)-equivariance for a popular point cloud architecture and produce state-of-the-art results on normal vector regression on point clouds.

KineticNet: Deep learning a transferable kinetic energy functional for orbital-free density functional theory

Orbital-free density functional theory (OF-DFT) holds the promise to compute ground state molecular properties at minimal cost. However, it has been held back by our inability to compute the kinetic energy as a functional of the electron density only. We here set out to learn the kinetic energy functional from ground truth provided by the more expensive Kohn-Sham density functional theory. Such learning is confronted with two key challenges: Giving the model sufficient expressivity and spatial context while limiting the memory footprint to afford computations on a GPU; and creating a sufficiently broad distribution of training data to enable iterative density optimization even when starting from a poor initial guess. In response, we introduce KineticNet, an equivariant deep neural network architecture based on point convolutions adapted to the prediction of quantities on molecular quadrature grids. Important contributions include convolution filters with sufficient spatial resolution in the vicinity of the nuclear cusp, an atom-centric sparse but expressive architecture that relays information across multiple bond lengths; and a new strategy to generate varied training data by finding ground state densities in the face of perturbations by a random external potential. KineticNet achieves, for the first time, chemical accuracy of the learned functionals across input densities and geometries of tiny molecules. For two electron systems, we additionally demonstrate OF-DFT density optimization with chemical accuracy.

Learning the Arrow of Time

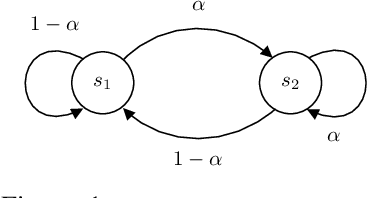
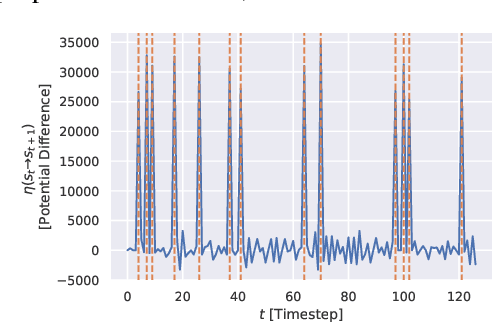
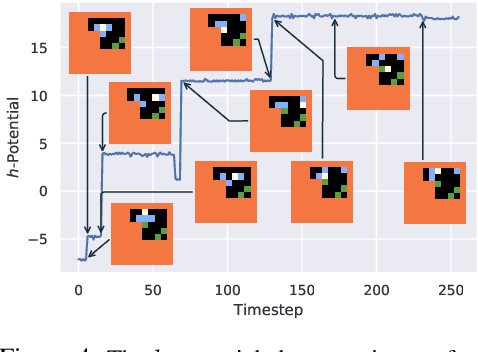
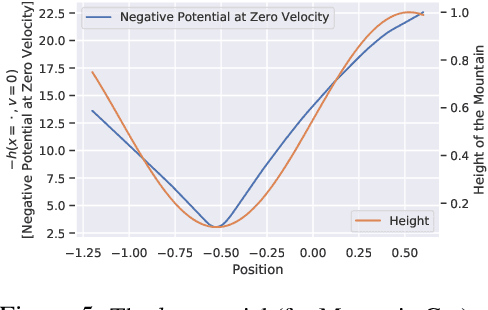
We humans seem to have an innate understanding of the asymmetric progression of time, which we use to efficiently and safely perceive and manipulate our environment. Drawing inspiration from that, we address the problem of learning an arrow of time in a Markov (Decision) Process. We illustrate how a learned arrow of time can capture meaningful information about the environment, which in turn can be used to measure reachability, detect side-effects and to obtain an intrinsic reward signal. We show empirical results on a selection of discrete and continuous environments, and demonstrate for a class of stochastic processes that the learned arrow of time agrees reasonably well with a known notion of an arrow of time given by the celebrated Jordan-Kinderlehrer-Otto result.