Semantic search for 100M+ galaxy images using AI-generated captions

Finding scientifically interesting phenomena through slow, manual labeling campaigns severely limits our ability to explore the billions of galaxy images produced by telescopes. In this work, we develop a pipeline to create a semantic search engine from completely unlabeled image data. Our method leverages Vision-Language Models (VLMs) to generate descriptions for galaxy images, then contrastively aligns a pre-trained multimodal astronomy foundation model with these embedded descriptions to produce searchable embeddings at scale. We find that current VLMs provide descriptions that are sufficiently informative to train a semantic search model that outperforms direct image similarity search. Our model, AION-Search, achieves state-of-the-art zero-shot performance on finding rare phenomena despite training on randomly selected images with no deliberate curation for rare cases. Furthermore, we introduce a VLM-based re-ranking method that nearly doubles the recall for our most challenging targets in the top-100 results. For the first time, AION-Search enables flexible semantic search scalable to 140 million galaxy images, enabling discovery from previously infeasible searches. More broadly, our work provides an approach for making large, unlabeled scientific image archives semantically searchable, expanding data exploration capabilities in fields from Earth observation to microscopy. The code, data, and app are publicly available at https://github.com/NolanKoblischke/AION-Search

Walrus: A Cross-Domain Foundation Model for Continuum Dynamics

Foundation models have transformed machine learning for language and vision, but achieving comparable impact in physical simulation remains a challenge. Data heterogeneity and unstable long-term dynamics inhibit learning from sufficiently diverse dynamics, while varying resolutions and dimensionalities challenge efficient training on modern hardware. Through empirical and theoretical analysis, we incorporate new approaches to mitigate these obstacles, including a harmonic-analysis-based stabilization method, load-balanced distributed 2D and 3D training strategies, and compute-adaptive tokenization. Using these tools, we develop Walrus, a transformer-based foundation model developed primarily for fluid-like continuum dynamics. Walrus is pretrained on nineteen diverse scenarios spanning astrophysics, geoscience, rheology, plasma physics, acoustics, and classical fluids. Experiments show that Walrus outperforms prior foundation models on both short and long term prediction horizons on downstream tasks and across the breadth of pretraining data, while ablation studies confirm the value of our contributions to forecast stability, training throughput, and transfer performance over conventional approaches. Code and weights are released for community use.

Geometric deep learning for galaxy-halo connection: a case study for galaxy intrinsic alignments

Forthcoming cosmological imaging surveys, such as the Rubin Observatory LSST, require large-scale simulations encompassing realistic galaxy populations for a variety of scientific applications. Of particular concern is the phenomenon of intrinsic alignments (IA), whereby galaxies orient themselves towards overdensities, potentially introducing significant systematic biases in weak gravitational lensing analyses if they are not properly modeled. Due to computational constraints, simulating the intricate details of galaxy formation and evolution relevant to IA across vast volumes is impractical. As an alternative, we propose a Deep Generative Model trained on the IllustrisTNG-100 simulation to sample 3D galaxy shapes and orientations to accurately reproduce intrinsic alignments along with correlated scalar features. We model the cosmic web as a set of graphs, each graph representing a halo with nodes representing the subhalos/galaxies. The architecture consists of a SO(3) $\times$ $\mathbb{R}^n$ diffusion generative model, for galaxy orientations and $n$ scalars, implemented with E(3) equivariant Graph Neural Networks that explicitly respect the Euclidean symmetries of our Universe. The model is able to learn and predict features such as galaxy orientations that are statistically consistent with the reference simulation. Notably, our model demonstrates the ability to jointly model Euclidean-valued scalars (galaxy sizes, shapes, and colors) along with non-Euclidean valued SO(3) quantities (galaxy orientations) that are governed by highly complex galactic physics at non-linear scales.

Unified framework for diffusion generative models in SO(3): applications in computer vision and astrophysics

Diffusion-based generative models represent the current state-of-the-art for image generation. However, standard diffusion models are based on Euclidean geometry and do not translate directly to manifold-valued data. In this work, we develop extensions of both score-based generative models (SGMs) and Denoising Diffusion Probabilistic Models (DDPMs) to the Lie group of 3D rotations, SO(3). SO(3) is of particular interest in many disciplines such as robotics, biochemistry and astronomy/cosmology science. Contrary to more general Riemannian manifolds, SO(3) admits a tractable solution to heat diffusion, and allows us to implement efficient training of diffusion models. We apply both SO(3) DDPMs and SGMs to synthetic densities on SO(3) and demonstrate state-of-the-art results. Additionally, we demonstrate the practicality of our model on pose estimation tasks and in predicting correlated galaxy orientations for astrophysics/cosmology.

Multiple Physics Pretraining for Physical Surrogate Models

We introduce multiple physics pretraining (MPP), an autoregressive task-agnostic pretraining approach for physical surrogate modeling. MPP involves training large surrogate models to predict the dynamics of multiple heterogeneous physical systems simultaneously by learning features that are broadly useful across diverse physical tasks. In order to learn effectively in this setting, we introduce a shared embedding and normalization strategy that projects the fields of multiple systems into a single shared embedding space. We validate the efficacy of our approach on both pretraining and downstream tasks over a broad fluid mechanics-oriented benchmark. We show that a single MPP-pretrained transformer is able to match or outperform task-specific baselines on all pretraining sub-tasks without the need for finetuning. For downstream tasks, we demonstrate that finetuning MPP-trained models results in more accurate predictions across multiple time-steps on new physics compared to training from scratch or finetuning pretrained video foundation models. We open-source our code and model weights trained at multiple scales for reproducibility and community experimentation.

xVal: A Continuous Number Encoding for Large Language Models

Large Language Models have not yet been broadly adapted for the analysis of scientific datasets due in part to the unique difficulties of tokenizing numbers. We propose xVal, a numerical encoding scheme that represents any real number using just a single token. xVal represents a given real number by scaling a dedicated embedding vector by the number value. Combined with a modified number-inference approach, this strategy renders the model end-to-end continuous when considered as a map from the numbers of the input string to those of the output string. This leads to an inductive bias that is generally more suitable for applications in scientific domains. We empirically evaluate our proposal on a number of synthetic and real-world datasets. Compared with existing number encoding schemes, we find that xVal is more token-efficient and demonstrates improved generalization.

AstroCLIP: Cross-Modal Pre-Training for Astronomical Foundation Models

We present AstroCLIP, a strategy to facilitate the construction of astronomical foundation models that bridge the gap between diverse observational modalities. We demonstrate that a cross-modal contrastive learning approach between images and optical spectra of galaxies yields highly informative embeddings of both modalities. In particular, we apply our method on multi-band images and optical spectra from the Dark Energy Spectroscopic Instrument (DESI), and show that: (1) these embeddings are well-aligned between modalities and can be used for accurate cross-modal searches, and (2) these embeddings encode valuable physical information about the galaxies -- in particular redshift and stellar mass -- that can be used to achieve competitive zero- and few- shot predictions without further finetuning. Additionally, in the process of developing our approach, we also construct a novel, transformer-based model and pretraining approach for processing galaxy spectra.

Towards solving model bias in cosmic shear forward modeling

As the volume and quality of modern galaxy surveys increase, so does the difficulty of measuring the cosmological signal imprinted in galaxy shapes. Weak gravitational lensing sourced by the most massive structures in the Universe generates a slight shearing of galaxy morphologies called cosmic shear, key probe for cosmological models. Modern techniques of shear estimation based on statistics of ellipticity measurements suffer from the fact that the ellipticity is not a well-defined quantity for arbitrary galaxy light profiles, biasing the shear estimation. We show that a hybrid physical and deep learning Hierarchical Bayesian Model, where a generative model captures the galaxy morphology, enables us to recover an unbiased estimate of the shear on realistic galaxies, thus solving the model bias.

Probabilistic Mass Mapping with Neural Score Estimation

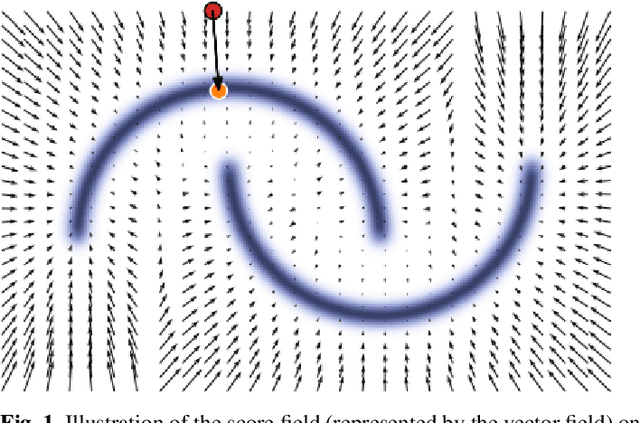
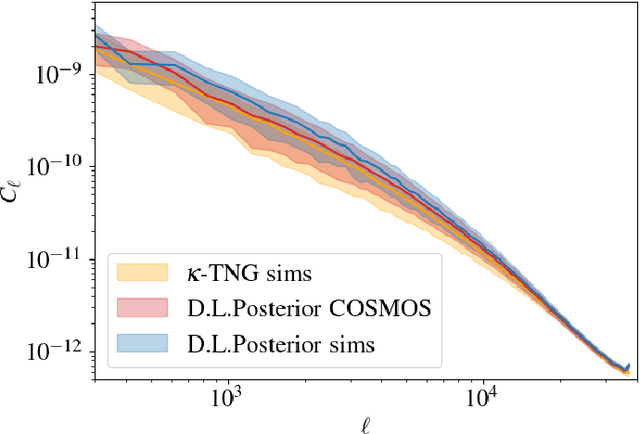
Weak lensing mass-mapping is a useful tool to access the full distribution of dark matter on the sky, but because of intrinsic galaxy ellipticies and finite fields/missing data, the recovery of dark matter maps constitutes a challenging ill-posed inverse problem. We introduce a novel methodology allowing for efficient sampling of the high-dimensional Bayesian posterior of the weak lensing mass-mapping problem, and relying on simulations for defining a fully non-Gaussian prior. We aim to demonstrate the accuracy of the method on simulations, and then proceed to applying it to the mass reconstruction of the HST/ACS COSMOS field. The proposed methodology combines elements of Bayesian statistics, analytic theory, and a recent class of Deep Generative Models based on Neural Score Matching. This approach allows us to do the following: 1) Make full use of analytic cosmological theory to constrain the 2pt statistics of the solution. 2) Learn from cosmological simulations any differences between this analytic prior and full simulations. 3) Obtain samples from the full Bayesian posterior of the problem for robust Uncertainty Quantification. We demonstrate the method on the $\kappa$TNG simulations and find that the posterior mean significantly outperfoms previous methods (Kaiser-Squires, Wiener filter, Sparsity priors) both on root-mean-square error and in terms of the Pearson correlation. We further illustrate the interpretability of the recovered posterior by establishing a close correlation between posterior convergence values and SNR of clusters artificially introduced into a field. Finally, we apply the method to the reconstruction of the HST/ACS COSMOS field and yield the highest quality convergence map of this field to date.

Adaptive wavelet distillation from neural networks through interpretations

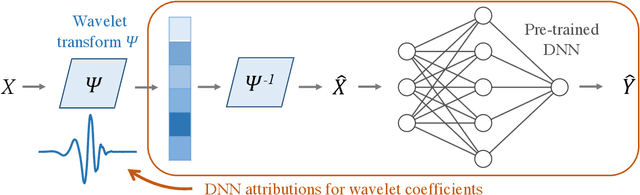
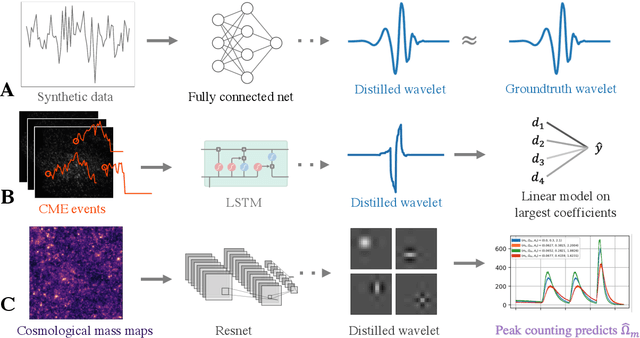
Recent deep-learning models have achieved impressive prediction performance, but often sacrifice interpretability and computational efficiency. Interpretability is crucial in many disciplines, such as science and medicine, where models must be carefully vetted or where interpretation is the goal itself. Moreover, interpretable models are concise and often yield computational efficiency. Here, we propose adaptive wavelet distillation (AWD), a method which aims to distill information from a trained neural network into a wavelet transform. Specifically, AWD penalizes feature attributions of a neural network in the wavelet domain to learn an effective multi-resolution wavelet transform. The resulting model is highly predictive, concise, computationally efficient, and has properties (such as a multi-scale structure) which make it easy to interpret. In close collaboration with domain experts, we showcase how AWD addresses challenges in two real-world settings: cosmological parameter inference and molecular-partner prediction. In both cases, AWD yields a scientifically interpretable and concise model which gives predictive performance better than state-of-the-art neural networks. Moreover, AWD identifies predictive features that are scientifically meaningful in the context of respective domains. All code and models are released in a full-fledged package available on Github (https://github.com/Yu-Group/adaptive-wavelets).