Francisca Vasconcelos
A Quadratic Speedup in Finding Nash Equilibria of Quantum Zero-Sum Games
Nov 17, 2023Abstract:Recent developments in domains such as non-local games, quantum interactive proofs, and quantum generative adversarial networks have renewed interest in quantum game theory and, specifically, quantum zero-sum games. Central to classical game theory is the efficient algorithmic computation of Nash equilibria, which represent optimal strategies for both players. In 2008, Jain and Watrous proposed the first classical algorithm for computing equilibria in quantum zero-sum games using the Matrix Multiplicative Weight Updates (MMWU) method to achieve a convergence rate of $\mathcal{O}(d/\epsilon^2)$ iterations to $\epsilon$-Nash equilibria in the $4^d$-dimensional spectraplex. In this work, we propose a hierarchy of quantum optimization algorithms that generalize MMWU via an extra-gradient mechanism. Notably, within this proposed hierarchy, we introduce the Optimistic Matrix Multiplicative Weights Update (OMMWU) algorithm and establish its average-iterate convergence complexity as $\mathcal{O}(d/\epsilon)$ iterations to $\epsilon$-Nash equilibria. This quadratic speed-up relative to Jain and Watrous' original algorithm sets a new benchmark for computing $\epsilon$-Nash equilibria in quantum zero-sum games.
UncertaINR: Uncertainty Quantification of End-to-End Implicit Neural Representations for Computed Tomography
Feb 22, 2022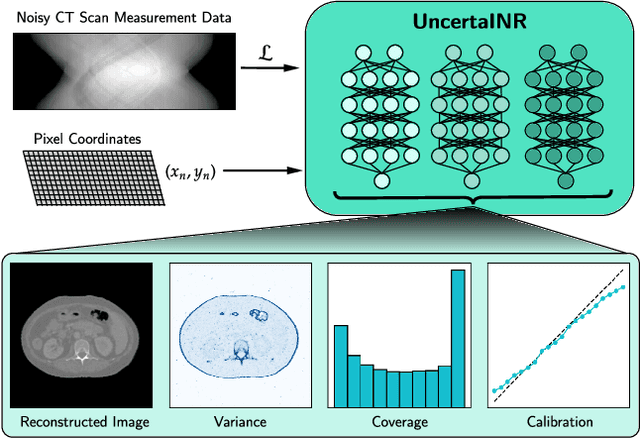
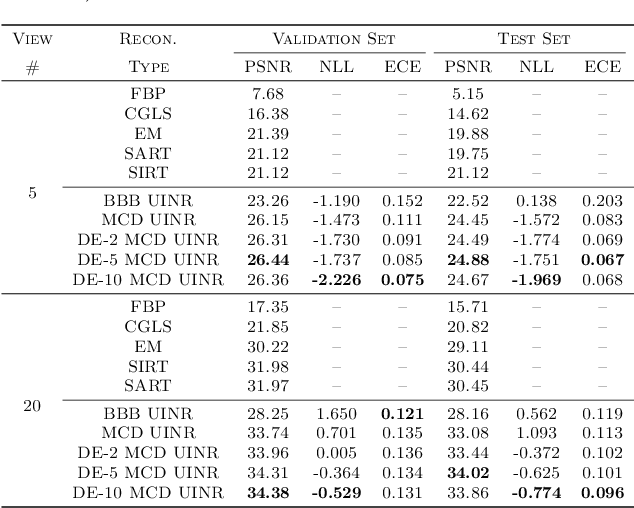
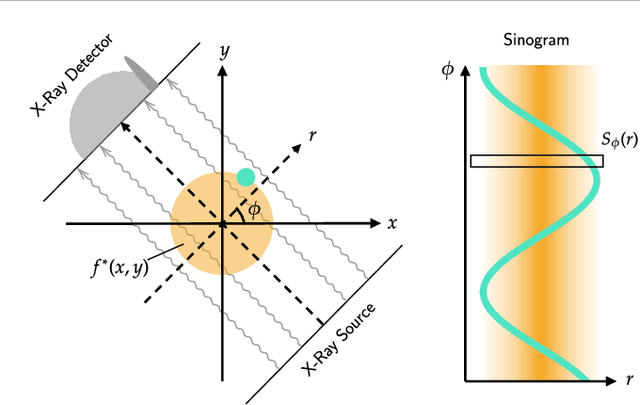
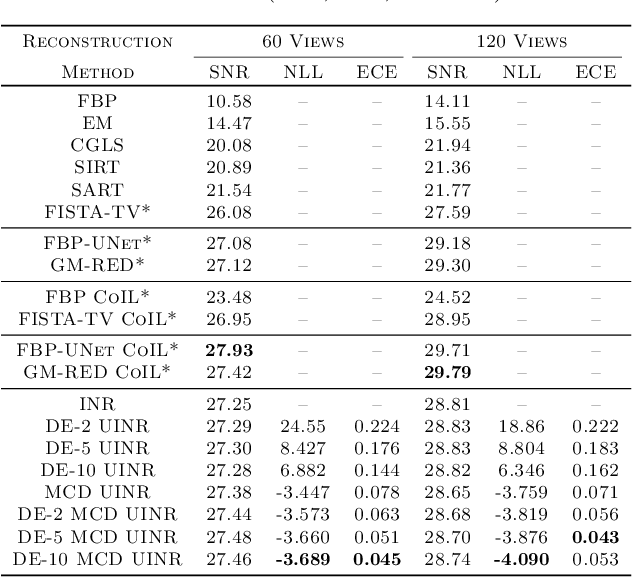
Abstract:Implicit neural representations (INRs) have achieved impressive results for scene reconstruction and computer graphics, where their performance has primarily been assessed on reconstruction accuracy. However, in medical imaging, where the reconstruction problem is underdetermined and model predictions inform high-stakes diagnoses, uncertainty quantification of INR inference is critical. To that end, we study UncertaINR: a Bayesian reformulation of INR-based image reconstruction, for computed tomography (CT). We test several Bayesian deep learning implementations of UncertaINR and find that they achieve well-calibrated uncertainty, while retaining accuracy competitive with other classical, INR-based, and CNN-based reconstruction techniques. In contrast to the best-performing prior approaches, UncertaINR does not require a large training dataset, but only a handful of validation images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge