A Heavy-Tailed Algebra for Probabilistic Programming

Despite the successes of probabilistic models based on passing noise through neural networks, recent work has identified that such methods often fail to capture tail behavior accurately, unless the tails of the base distribution are appropriately calibrated. To overcome this deficiency, we propose a systematic approach for analyzing the tails of random variables, and we illustrate how this approach can be used during the static analysis (before drawing samples) pass of a probabilistic programming language compiler. To characterize how the tails change under various operations, we develop an algebra which acts on a three-parameter family of tail asymptotics and which is based on the generalized Gamma distribution. Our algebraic operations are closed under addition and multiplication; they are capable of distinguishing sub-Gaussians with differing scales; and they handle ratios sufficiently well to reproduce the tails of most important statistical distributions directly from their definitions. Our empirical results confirm that inference algorithms that leverage our heavy-tailed algebra attain superior performance across a number of density modeling and variational inference tasks.

Fat-Tailed Variational Inference with Anisotropic Tail Adaptive Flows

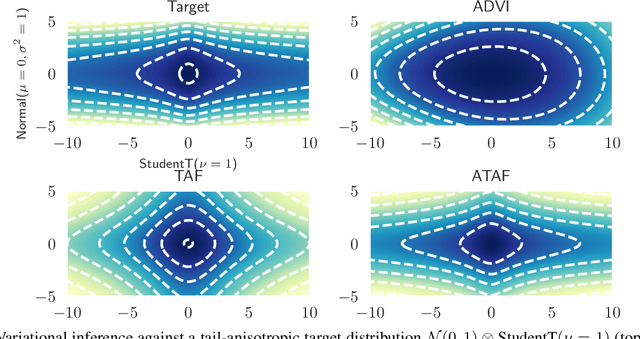
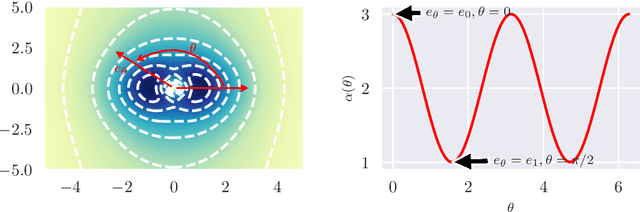
While fat-tailed densities commonly arise as posterior and marginal distributions in robust models and scale mixtures, they present challenges when Gaussian-based variational inference fails to capture tail decay accurately. We first improve previous theory on tails of Lipschitz flows by quantifying how the tails affect the rate of tail decay and by expanding the theory to non-Lipschitz polynomial flows. Then, we develop an alternative theory for multivariate tail parameters which is sensitive to tail-anisotropy. In doing so, we unveil a fundamental problem which plagues many existing flow-based methods: they can only model tail-isotropic distributions (i.e., distributions having the same tail parameter in every direction). To mitigate this and enable modeling of tail-anisotropic targets, we propose anisotropic tail-adaptive flows (ATAF). Experimental results on both synthetic and real-world targets confirm that ATAF is competitive with prior work while also exhibiting appropriate tail-anisotropy.

Accelerating Metropolis-Hastings with Lightweight Inference Compilation

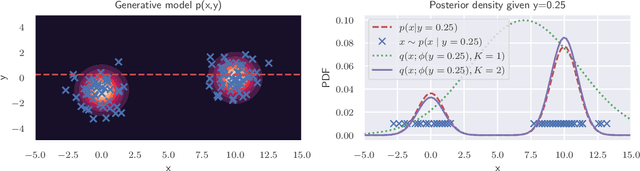
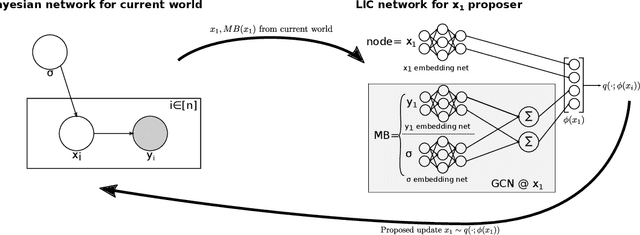
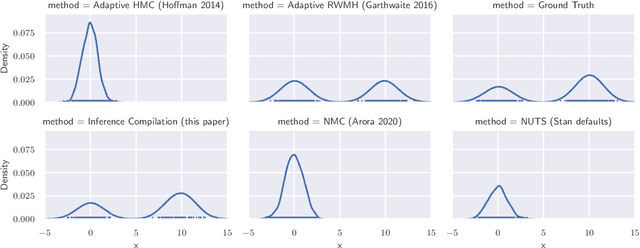
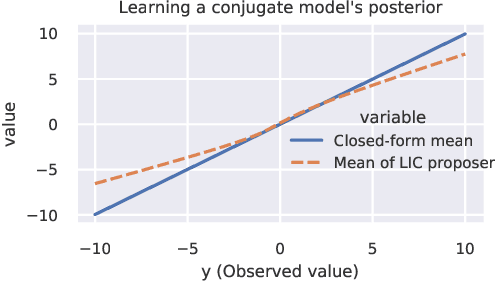
In order to construct accurate proposers for Metropolis-Hastings Markov Chain Monte Carlo, we integrate ideas from probabilistic graphical models and neural networks in an open-source framework we call Lightweight Inference Compilation (LIC). LIC implements amortized inference within an open-universe declarative probabilistic programming language (PPL). Graph neural networks are used to parameterize proposal distributions as functions of Markov blankets, which during "compilation" are optimized to approximate single-site Gibbs sampling distributions. Unlike prior work in inference compilation (IC), LIC forgoes importance sampling of linear execution traces in favor of operating directly on Bayesian networks. Through using a declarative PPL, the Markov blankets of nodes (which may be non-static) are queried at inference-time to produce proposers Experimental results show LIC can produce proposers which have less parameters, greater robustness to nuisance random variables, and improved posterior sampling in a Bayesian logistic regression and $n$-schools inference application.

Precise expressions for random projections: Low-rank approximation and randomized Newton

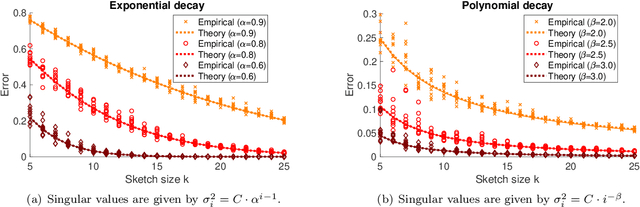
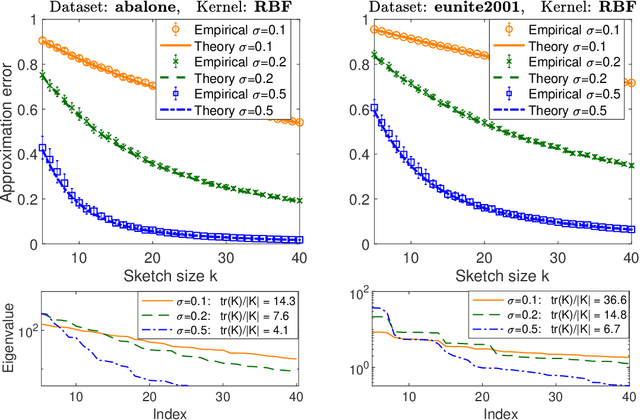
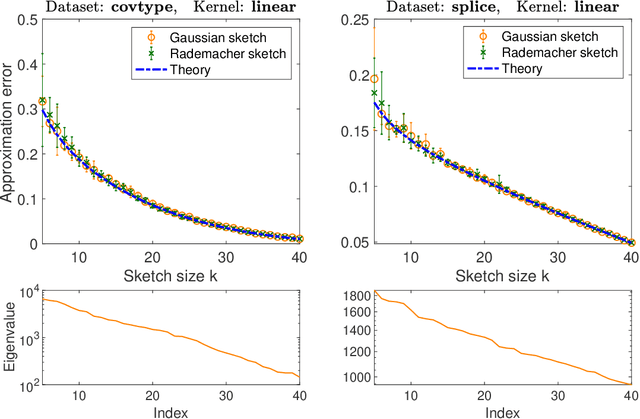
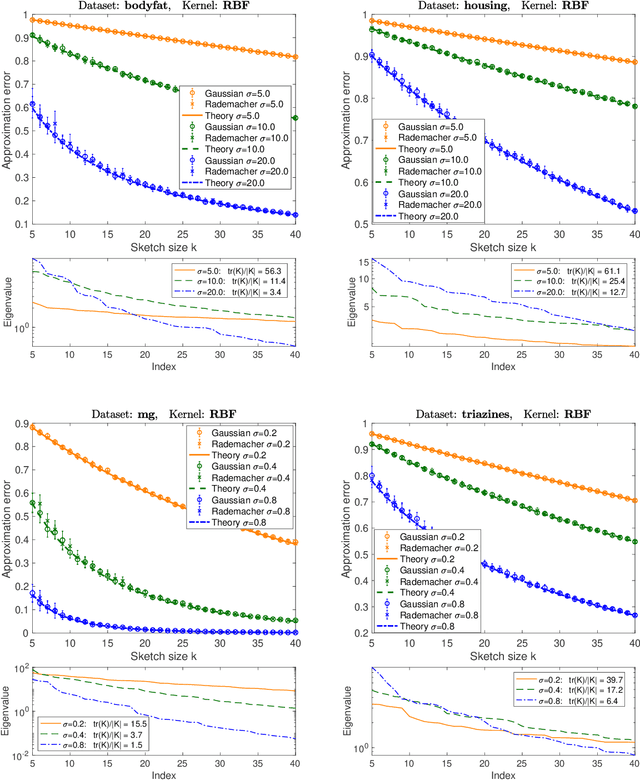
It is often desirable to reduce the dimensionality of a large dataset by projecting it onto a low-dimensional subspace. Matrix sketching has emerged as a powerful technique for performing such dimensionality reduction very efficiently. Even though there is an extensive literature on the worst-case performance of sketching, existing guarantees are typically very different from what is observed in practice. We exploit recent developments in the spectral analysis of random matrices to develop novel techniques that provide provably accurate expressions for the expected value of random projection matrices obtained via sketching. These expressions can be used to characterize the performance of dimensionality reduction in a variety of common machine learning tasks, ranging from low-rank approximation to iterative stochastic optimization. Our results apply to several popular sketching methods, including Gaussian and Rademacher sketches, and they enable precise analysis of these methods in terms of spectral properties of the data. Empirical results show that the expressions we derive reflect the practical performance of these sketching methods, down to lower-order effects and even constant factors.

Exact expressions for double descent and implicit regularization via surrogate random design

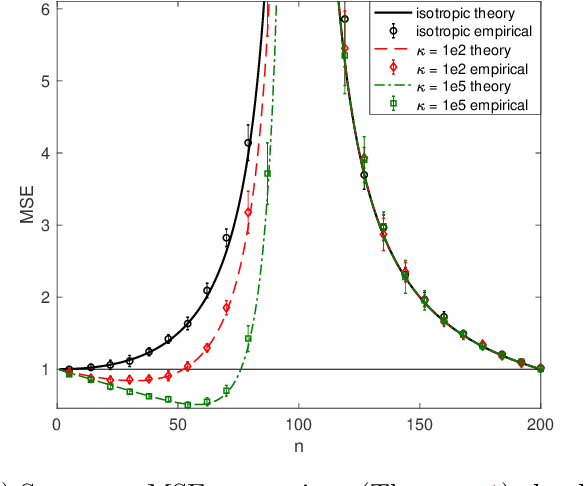
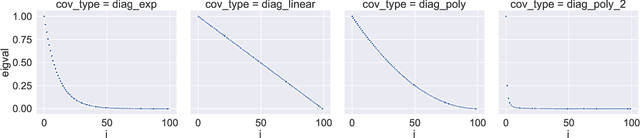
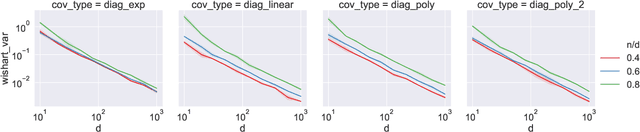
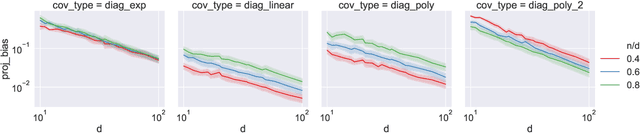
Double descent refers to the phase transition that is exhibited by the generalization error of unregularized learning models when varying the ratio between the number of parameters and the number of training samples. The recent success of highly over-parameterized machine learning models such as deep neural networks has motivated a theoretical analysis of the double descent phenomenon in classical models such as linear regression which can also generalize well in the over-parameterized regime. We build on recent advances in Randomized Numerical Linear Algebra (RandNLA) to provide the first exact non-asymptotic expressions for double descent of the minimum norm linear estimator. Our approach involves constructing what we call a surrogate random design to replace the standard i.i.d. design of the training sample. This surrogate design admits exact expressions for the mean squared error of the estimator while preserving the key properties of the standard design. We also establish an exact implicit regularization result for over-parameterized training samples. In particular, we show that, for the surrogate design, the implicit bias of the unregularized minimum norm estimator precisely corresponds to solving a ridge-regularized least squares problem on the population distribution.

Bayesian experimental design using regularized determinantal point processes

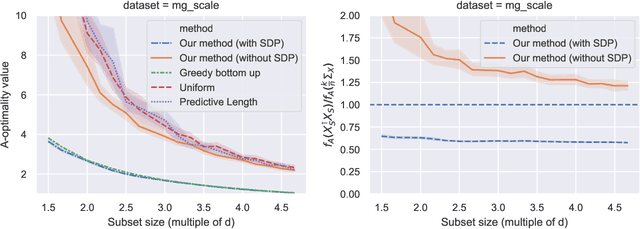
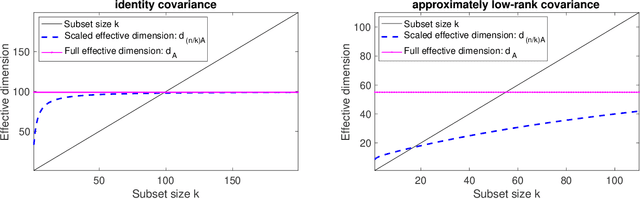
In experimental design, we are given $n$ vectors in $d$ dimensions, and our goal is to select $k\ll n$ of them to perform expensive measurements, e.g., to obtain labels/responses, for a linear regression task. Many statistical criteria have been proposed for choosing the optimal design, with popular choices including A- and D-optimality. If prior knowledge is given, typically in the form of a $d\times d$ precision matrix $\mathbf A$, then all of the criteria can be extended to incorporate that information via a Bayesian framework. In this paper, we demonstrate a new fundamental connection between Bayesian experimental design and determinantal point processes, the latter being widely used for sampling diverse subsets of data. We use this connection to develop new efficient algorithms for finding $(1+\epsilon)$-approximations of optimal designs under four optimality criteria: A, C, D and V. Our algorithms can achieve this when the desired subset size $k$ is $\Omega(\frac{d_{\mathbf A}}{\epsilon} + \frac{\log 1/\epsilon}{\epsilon^2})$, where $d_{\mathbf A}\leq d$ is the $\mathbf A$-effective dimension, which can often be much smaller than $d$. Our results offer direct improvements over a number of prior works, for both Bayesian and classical experimental design, in terms of algorithm efficiency, approximation quality, and range of applicable criteria.