Accelerating Metropolis-Hastings with Lightweight Inference Compilation

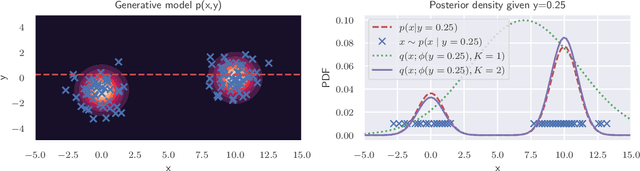
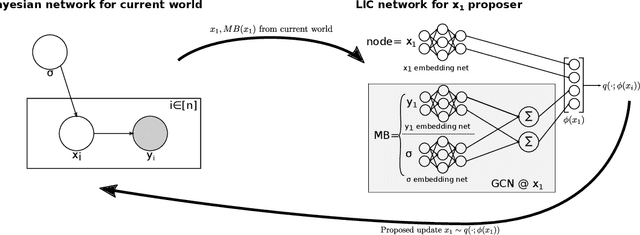
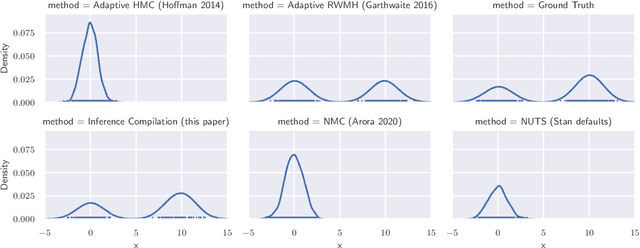
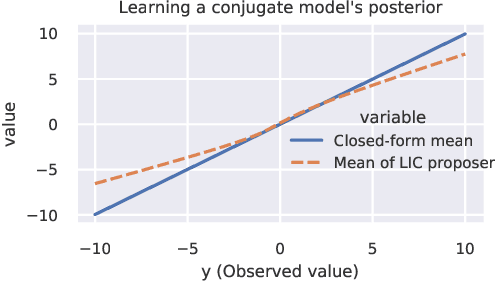
In order to construct accurate proposers for Metropolis-Hastings Markov Chain Monte Carlo, we integrate ideas from probabilistic graphical models and neural networks in an open-source framework we call Lightweight Inference Compilation (LIC). LIC implements amortized inference within an open-universe declarative probabilistic programming language (PPL). Graph neural networks are used to parameterize proposal distributions as functions of Markov blankets, which during "compilation" are optimized to approximate single-site Gibbs sampling distributions. Unlike prior work in inference compilation (IC), LIC forgoes importance sampling of linear execution traces in favor of operating directly on Bayesian networks. Through using a declarative PPL, the Markov blankets of nodes (which may be non-static) are queried at inference-time to produce proposers Experimental results show LIC can produce proposers which have less parameters, greater robustness to nuisance random variables, and improved posterior sampling in a Bayesian logistic regression and $n$-schools inference application.

PPL Bench: Evaluation Framework For Probabilistic Programming Languages

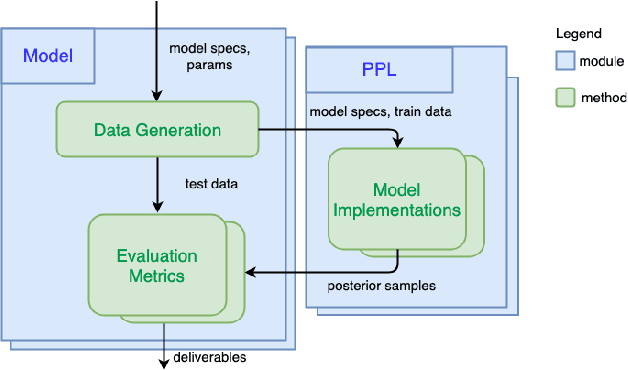
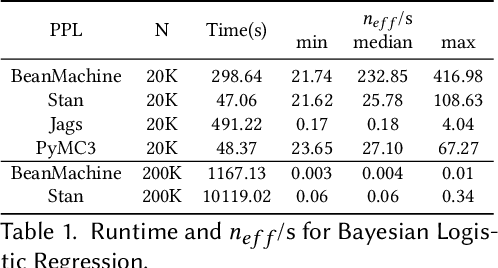
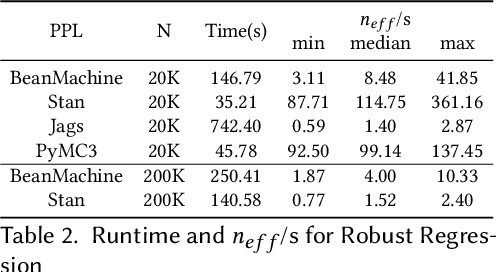
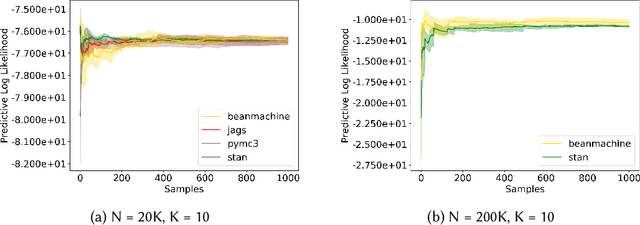
We introduce PPL Bench, a new benchmark for evaluating Probabilistic Programming Languages (PPLs) on a variety of statistical models. The benchmark includes data generation and evaluation code for a number of models as well as implementations in some common PPLs. All of the benchmark code and PPL implementations are available on Github. We welcome contributions of new models and PPLs and as well as improvements in existing PPL implementations. The purpose of the benchmark is two-fold. First, we want researchers as well as conference reviewers to be able to evaluate improvements in PPLs in a standardized setting. Second, we want end users to be able to pick the PPL that is most suited for their modeling application. In particular, we are interested in evaluating the accuracy and speed of convergence of the inferred posterior. Each PPL only needs to provide posterior samples given a model and observation data. The framework automatically computes and plots growth in predictive log-likelihood on held out data in addition to reporting other common metrics such as effective sample size and $\hat{r}$.