Combinatorial Sleeping Bandits with Fairness Constraints
Paper and Code
Jan 18, 2019
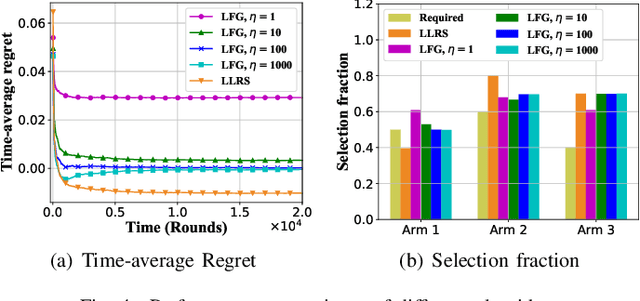


The multi-armed bandit (MAB) model has been widely adopted for studying many practical optimization problems (network resource allocation, ad placement, crowdsourcing, etc.) with unknown parameters. The goal of the player here is to maximize the cumulative reward in the face of uncertainty. However, the basic MAB model neglects several important factors of the system in many real-world applications, where multiple arms can be simultaneously played and an arm could sometimes be "sleeping". Besides, ensuring fairness is also a key design concern in practice. To that end, we propose a new Combinatorial Sleeping MAB model with Fairness constraints, called CSMAB-F, aiming to address the aforementioned crucial modeling issues. The objective is now to maximize the reward while satisfying the fairness requirement of a minimum selection fraction for each individual arm. To tackle this new problem, we extend an online learning algorithm, UCB, to deal with a critical tradeoff between exploitation and exploration and employ the virtual queue technique to properly handle the fairness constraints. By carefully integrating these two techniques, we develop a new algorithm, called Learning with Fairness Guarantee (LFG), for the CSMAB-F problem. Further, we rigorously prove that not only LFG is feasibility-optimal, but it also has a time-average regret upper bounded by $\frac{N}{2\eta}+\frac{\beta_1\sqrt{mNT\log{T}}+\beta_2 N}{T}$, where N is the total number of arms, m is the maximum number of arms that can be simultaneously played, T is the time horizon, $\beta_1$ and $\beta_2$ are constants, and $\eta$ is a design parameter that we can tune. Finally, we perform extensive simulations to corroborate the effectiveness of the proposed algorithm. Interestingly, the simulation results reveal an important tradeoff between the regret and the speed of convergence to a point satisfying the fairness constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge