Aerial Image Classification in Scarce and Unconstrained Environments via Conformal Prediction

This paper presents a comprehensive empirical analysis of conformal prediction methods on a challenging aerial image dataset featuring diverse events in unconstrained environments. Conformal prediction is a powerful post-hoc technique that takes the output of any classifier and transforms it into a set of likely labels, providing a statistical guarantee on the coverage of the true label. Unlike evaluations on standard benchmarks, our study addresses the complexities of data-scarce and highly variable real-world settings. We investigate the effectiveness of leveraging pretrained models (MobileNet, DenseNet, and ResNet), fine-tuned with limited labeled data, to generate informative prediction sets. To further evaluate the impact of calibration, we consider two parallel pipelines (with and without temperature scaling) and assess performance using two key metrics: empirical coverage and average prediction set size. This setup allows us to systematically examine how calibration choices influence the trade-off between reliability and efficiency. Our findings demonstrate that even with relatively small labeled samples and simple nonconformity scores, conformal prediction can yield valuable uncertainty estimates for complex tasks. Moreover, our analysis reveals that while temperature scaling is often employed for calibration, it does not consistently lead to smaller prediction sets, underscoring the importance of careful consideration in its application. Furthermore, our results highlight the significant potential of model compression techniques within the conformal prediction pipeline for deployment in resource-constrained environments. Based on our observations, we advocate for future research to delve into the impact of noisy or ambiguous labels on conformal prediction performance and to explore effective model reduction strategies.

Probabilistic Neural Networks (PNNs) with t-Distributed Outputs: Adaptive Prediction Intervals Beyond Gaussian Assumptions

Traditional neural network regression models provide only point estimates, failing to capture predictive uncertainty. Probabilistic neural networks (PNNs) address this limitation by producing output distributions, enabling the construction of prediction intervals. However, the common assumption of Gaussian output distributions often results in overly wide intervals, particularly in the presence of outliers or deviations from normality. To enhance the adaptability of PNNs, we propose t-Distributed Neural Networks (TDistNNs), which generate t-distributed outputs, parameterized by location, scale, and degrees of freedom. The degrees of freedom parameter allows TDistNNs to model heavy-tailed predictive distributions, improving robustness to non-Gaussian data and enabling more adaptive uncertainty quantification. We develop a novel loss function tailored for the t-distribution and derive efficient gradient computations for seamless integration into deep learning frameworks. Empirical evaluations on synthetic and real-world data demonstrate that TDistNNs improve the balance between coverage and interval width. Notably, for identical architectures, TDistNNs consistently produce narrower prediction intervals than Gaussian-based PNNs while maintaining proper coverage. This work contributes a flexible framework for uncertainty estimation in neural networks tasked with regression, particularly suited to settings involving complex output distributions.

Kolmogorov-Arnold Networks in Low-Data Regimes: A Comparative Study with Multilayer Perceptrons

Multilayer Perceptrons (MLPs) have long been a cornerstone in deep learning, known for their capacity to model complex relationships. Recently, Kolmogorov-Arnold Networks (KANs) have emerged as a compelling alternative, utilizing highly flexible learnable activation functions directly on network edges, a departure from the neuron-centric approach of MLPs. However, KANs significantly increase the number of learnable parameters, raising concerns about their effectiveness in data-scarce environments. This paper presents a comprehensive comparative study of MLPs and KANs from both algorithmic and experimental perspectives, with a focus on low-data regimes. We introduce an effective technique for designing MLPs with unique, parameterized activation functions for each neuron, enabling a more balanced comparison with KANs. Using empirical evaluations on simulated data and two real-world data sets from medicine and engineering, we explore the trade-offs between model complexity and accuracy, with particular attention to the role of network depth. Our findings show that MLPs with individualized activation functions achieve significantly higher predictive accuracy with only a modest increase in parameters, especially when the sample size is limited to around one hundred. For example, in a three-class classification problem within additive manufacturing, MLPs achieve a median accuracy of 0.91, significantly outperforming KANs, which only reach a median accuracy of 0.53 with default hyperparameters. These results offer valuable insights into the impact of activation function selection in neural networks.

Probabilistic Neural Networks (PNNs) for Modeling Aleatoric Uncertainty in Scientific Machine Learning

This paper investigates the use of probabilistic neural networks (PNNs) to model aleatoric uncertainty, which refers to the inherent variability in the input-output relationships of a system, often characterized by unequal variance or heteroscedasticity. Unlike traditional neural networks that produce deterministic outputs, PNNs generate probability distributions for the target variable, allowing the determination of both predicted means and intervals in regression scenarios. Contributions of this paper include the development of a probabilistic distance metric to optimize PNN architecture, and the deployment of PNNs in controlled data sets as well as a practical material science case involving fiber-reinforced composites. The findings confirm that PNNs effectively model aleatoric uncertainty, proving to be more appropriate than the commonly employed Gaussian process regression for this purpose. Specifically, in a real-world scientific machine learning context, PNNs yield remarkably accurate output mean estimates with R-squared scores approaching 0.97, and their predicted intervals exhibit a high correlation coefficient of nearly 0.80, closely matching observed data intervals. Hence, this research contributes to the ongoing exploration of leveraging the sophisticated representational capacity of neural networks to delineate complex input-output relationships in scientific problems.

Adaptive Activation Functions for Predictive Modeling with Sparse Experimental Data

A pivotal aspect in the design of neural networks lies in selecting activation functions, crucial for introducing nonlinear structures that capture intricate input-output patterns. While the effectiveness of adaptive or trainable activation functions has been studied in domains with ample data, like image classification problems, significant gaps persist in understanding their influence on classification accuracy and predictive uncertainty in settings characterized by limited data availability. This research aims to address these gaps by investigating the use of two types of adaptive activation functions. These functions incorporate shared and individual trainable parameters per hidden layer and are examined in three testbeds derived from additive manufacturing problems containing fewer than one hundred training instances. Our investigation reveals that adaptive activation functions, such as Exponential Linear Unit (ELU) and Softplus, with individual trainable parameters, result in accurate and confident prediction models that outperform fixed-shape activation functions and the less flexible method of using identical trainable activation functions in a hidden layer. Therefore, this work presents an elegant way of facilitating the design of adaptive neural networks in scientific and engineering problems.

Two-Stage Surrogate Modeling for Data-Driven Design Optimization with Application to Composite Microstructure Generation

This paper introduces a novel two-stage machine learning-based surrogate modeling framework to address inverse problems in scientific and engineering fields. In the first stage of the proposed framework, a machine learning model termed the "learner" identifies a limited set of candidates within the input design space whose predicted outputs closely align with desired outcomes. Subsequently, in the second stage, a separate surrogate model, functioning as an "evaluator," is employed to assess the reduced candidate space generated in the first stage. This evaluation process eliminates inaccurate and uncertain solutions, guided by a user-defined coverage level. The framework's distinctive contribution is the integration of conformal inference, providing a versatile and efficient approach that can be widely applicable. To demonstrate the effectiveness of the proposed framework compared to conventional single-stage inverse problems, we conduct several benchmark tests and investigate an engineering application focused on the micromechanical modeling of fiber-reinforced composites. The results affirm the superiority of our proposed framework, as it consistently produces more reliable solutions. Therefore, the introduced framework offers a unique perspective on fostering interactions between machine learning-based surrogate models in real-world applications.

D-CBRS: Accounting For Intra-Class Diversity in Continual Learning

Continual learning -- accumulating knowledge from a sequence of learning experiences -- is an important yet challenging problem. In this paradigm, the model's performance for previously encountered instances may substantially drop as additional data are seen. When dealing with class-imbalanced data, forgetting is further exacerbated. Prior work has proposed replay-based approaches which aim at reducing forgetting by intelligently storing instances for future replay. Although Class-Balancing Reservoir Sampling (CBRS) has been successful in dealing with imbalanced data, the intra-class diversity has not been accounted for, implicitly assuming that each instance of a class is equally informative. We present Diverse-CBRS (D-CBRS), an algorithm that allows us to consider within class diversity when storing instances in the memory. Our results show that D-CBRS outperforms state-of-the-art memory management continual learning algorithms on data sets with considerable intra-class diversity.

An Empirical Evaluation of the t-SNE Algorithm for Data Visualization in Structural Engineering

A fundamental task in machine learning involves visualizing high-dimensional data sets that arise in high-impact application domains. When considering the context of large imbalanced data, this problem becomes much more challenging. In this paper, the t-Distributed Stochastic Neighbor Embedding (t-SNE) algorithm is used to reduce the dimensions of an earthquake engineering related data set for visualization purposes. Since imbalanced data sets greatly affect the accuracy of classifiers, we employ Synthetic Minority Oversampling Technique (SMOTE) to tackle the imbalanced nature of such data set. We present the result obtained from t-SNE and SMOTE and compare it to the basic approaches with various aspects. Considering four options and six classification algorithms, we show that using t-SNE on the imbalanced data and SMOTE on the training data set, neural network classifiers have promising results without sacrificing accuracy. Hence, we can transform the studied scientific data into a two-dimensional (2D) space, enabling the visualization of the classifier and the resulting decision surface using a 2D plot.

Kernel Ridge Regression Using Importance Sampling with Application to Seismic Response Prediction

Scalable kernel methods, including kernel ridge regression, often rely on low-rank matrix approximations using the Nystrom method, which involves selecting landmark points from large data sets. The existing approaches to selecting landmarks are typically computationally demanding as they require manipulating and performing computations with large matrices in the input or feature space. In this paper, our contribution is twofold. The first contribution is to propose a novel landmark selection method that promotes diversity using an efficient two-step approach. Our landmark selection technique follows a coarse to fine strategy, where the first step computes importance scores with a single pass over the whole data. The second step performs K-means clustering on the constructed coreset to use the obtained centroids as landmarks. Hence, the introduced method provides tunable trade-offs between accuracy and efficiency. Our second contribution is to investigate the performance of several landmark selection techniques using a novel application of kernel methods for predicting structural responses due to earthquake load and material uncertainties. Our experiments exhibit the merits of our proposed landmark selection scheme against baselines.

A Unified NMPC Scheme for MAVs Navigation with 3D Collision Avoidance under Position Uncertainty

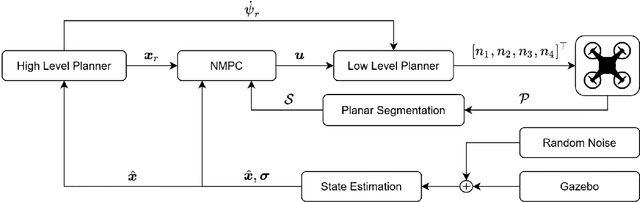
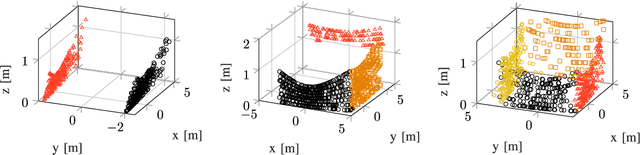
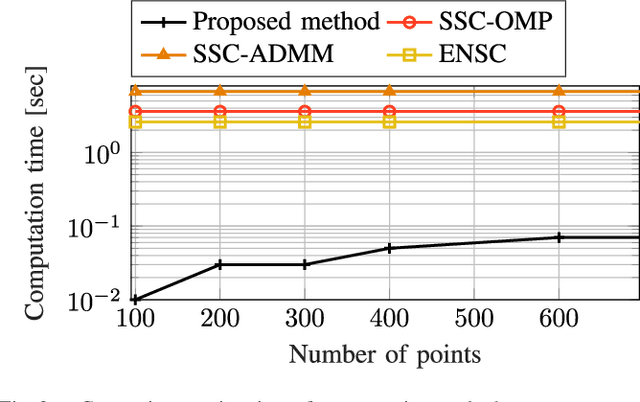
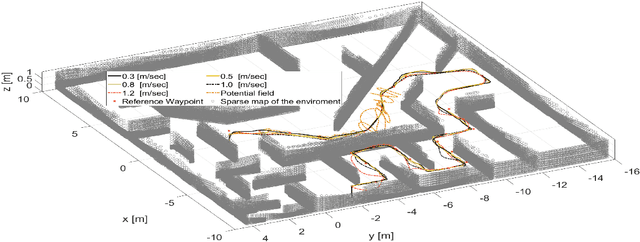
This article proposes a novel Nonlinear Model Predictive Control (NMPC) framework for Micro Aerial Vehicle (MAV) autonomous navigation in constrained environments. The introduced framework allows us to consider the nonlinear dynamics of MAVs and guarantees real-time performance. Our first contribution is to design a computationally efficient subspace clustering method to reveal from geometrical constraints to underlying constraint planes within a 3D point cloud, obtained from a 3D lidar scanner. The second contribution of our work is to incorporate the extracted information into the nonlinear constraints of NMPC for avoiding collisions. Our third contribution focuses on making the controller robust by considering the uncertainty of localization and NMPC using the Shannon entropy. This step enables us to track either the position or velocity references, or none of them if necessary. As a result, the collision avoidance constraints are defined in the local coordinates of MAVs and it remains active and guarantees collision avoidance, despite localization uncertainties, e.g., position estimation drifts. Additionally, as the platform continues the mission, this will result in less uncertain position estimations, due to the feature extraction and loop closure. The efficacy of the suggested framework has been evaluated using various simulations in the Gazebo environment.