Tree-Wasserstein Distance for High Dimensional Data with a Latent Feature Hierarchy

Finding meaningful distances between high-dimensional data samples is an important scientific task. To this end, we propose a new tree-Wasserstein distance (TWD) for high-dimensional data with two key aspects. First, our TWD is specifically designed for data with a latent feature hierarchy, i.e., the features lie in a hierarchical space, in contrast to the usual focus on embedding samples in hyperbolic space. Second, while the conventional use of TWD is to speed up the computation of the Wasserstein distance, we use its inherent tree as a means to learn the latent feature hierarchy. The key idea of our method is to embed the features into a multi-scale hyperbolic space using diffusion geometry and then present a new tree decoding method by establishing analogies between the hyperbolic embedding and trees. We show that our TWD computed based on data observations provably recovers the TWD defined with the latent feature hierarchy and that its computation is efficient and scalable. We showcase the usefulness of the proposed TWD in applications to word-document and single-cell RNA-sequencing datasets, demonstrating its advantages over existing TWDs and methods based on pre-trained models.

On Learning what to Learn: heterogeneous observations of dynamics and establishing (possibly causal) relations among them

Before we attempt to learn a function between two (sets of) observables of a physical process, we must first decide what the inputs and what the outputs of the desired function are going to be. Here we demonstrate two distinct, data-driven ways of initially deciding ``the right quantities'' to relate through such a function, and then proceed to learn it. This is accomplished by processing multiple simultaneous heterogeneous data streams (ensembles of time series) from observations of a physical system: multiple observation processes of the system. We thus determine (a) what subsets of observables are common between the observation processes (and therefore observable from each other, relatable through a function); and (b) what information is unrelated to these common observables, and therefore particular to each observation process, and not contributing to the desired function. Any data-driven function approximation technique can subsequently be used to learn the input-output relation, from k-nearest neighbors and Geometric Harmonics to Gaussian Processes and Neural Networks. Two particular ``twists'' of the approach are discussed. The first has to do with the identifiability of particular quantities of interest from the measurements. We now construct mappings from a single set of observations of one process to entire level sets of measurements of the process, consistent with this single set. The second attempts to relate our framework to a form of causality: if one of the observation processes measures ``now'', while the second observation process measures ``in the future'', the function to be learned among what is common across observation processes constitutes a dynamical model for the system evolution.

Gappy local conformal auto-encoders for heterogeneous data fusion: in praise of rigidity

Fusing measurements from multiple, heterogeneous, partial sources, observing a common object or process, poses challenges due to the increasing availability of numbers and types of sensors. In this work we propose, implement and validate an end-to-end computational pipeline in the form of a multiple-auto-encoder neural network architecture for this task. The inputs to the pipeline are several sets of partial observations, and the result is a globally consistent latent space, harmonizing (rigidifying, fusing) all measurements. The key enabler is the availability of multiple slightly perturbed measurements of each instance:, local measurement, "bursts", that allows us to estimate the local distortion induced by each instrument. We demonstrate the approach in a sequence of examples, starting with simple two-dimensional data sets and proceeding to a Wi-Fi localization problem and to the solution of a "dynamical puzzle" arising in spatio-temporal observations of the solutions of Partial Differential Equations.

Hyperbolic Diffusion Embedding and Distance for Hierarchical Representation Learning

Finding meaningful representations and distances of hierarchical data is important in many fields. This paper presents a new method for hierarchical data embedding and distance. Our method relies on combining diffusion geometry, a central approach to manifold learning, and hyperbolic geometry. Specifically, using diffusion geometry, we build multi-scale densities on the data, aimed to reveal their hierarchical structure, and then embed them into a product of hyperbolic spaces. We show theoretically that our embedding and distance recover the underlying hierarchical structure. In addition, we demonstrate the efficacy of the proposed method and its advantages compared to existing methods on graph embedding benchmarks and hierarchical datasets.

A common variable minimax theorem for graphs

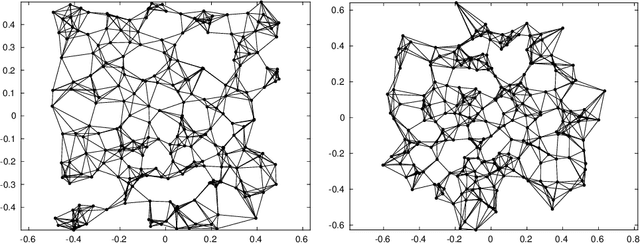
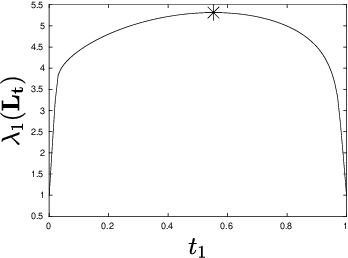
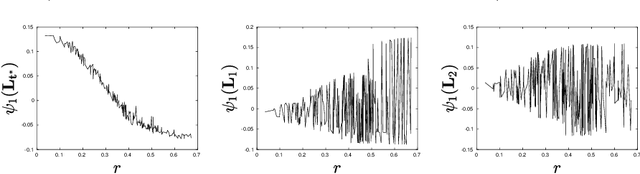
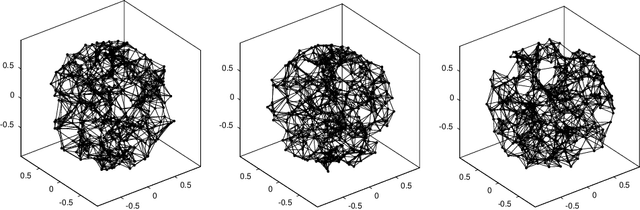
Let $\mathcal{G} = \{G_1 = (V, E_1), \dots, G_m = (V, E_m)\}$ be a collection of $m$ graphs defined on a common set of vertices $V$ but with different edge sets $E_1, \dots, E_m$. Informally, a function $f :V \rightarrow \mathbb{R}$ is smooth with respect to $G_k = (V,E_k)$ if $f(u) \sim f(v)$ whenever $(u, v) \in E_k$. We study the problem of understanding whether there exists a nonconstant function that is smooth with respect to all graphs in $\mathcal{G}$, simultaneously, and how to find it if it exists.

Doubly-Stochastic Normalization of the Gaussian Kernel is Robust to Heteroskedastic Noise

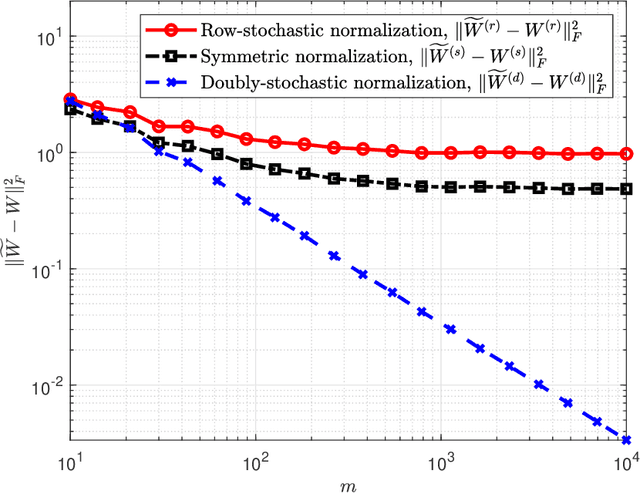
A fundamental step in many data-analysis techniques is the construction of an affinity matrix describing similarities between data points. When the data points reside in Euclidean space, a widespread approach is to from an affinity matrix by the Gaussian kernel with pairwise distances, and to follow with a certain normalization (e.g. the row-stochastic normalization or its symmetric variant). We demonstrate that the doubly-stochastic normalization of the Gaussian kernel with zero main diagonal (i.e. no self loops) is robust to heteroskedastic noise. That is, the doubly-stochastic normalization is advantageous in that it automatically accounts for observations with different noise variances. Specifically, we prove that in a suitable high-dimensional setting where heteroskedastic noise does not concentrate too much in any particular direction in space, the resulting (doubly-stochastic) noisy affinity matrix converges to its clean counterpart with rate $m^{-1/2}$, where $m$ is the ambient dimension. We demonstrate this result numerically, and show that in contrast, the popular row-stochastic and symmetric normalizations behave unfavorably under heteroskedastic noise. Furthermore, we provide a prototypical example of simulated single-cell RNA sequence data with strong intrinsic heteroskedasticity, where the advantage of the doubly-stochastic normalization for exploratory analysis is evident.

LOCA: LOcal Conformal Autoencoder for standardized data coordinates

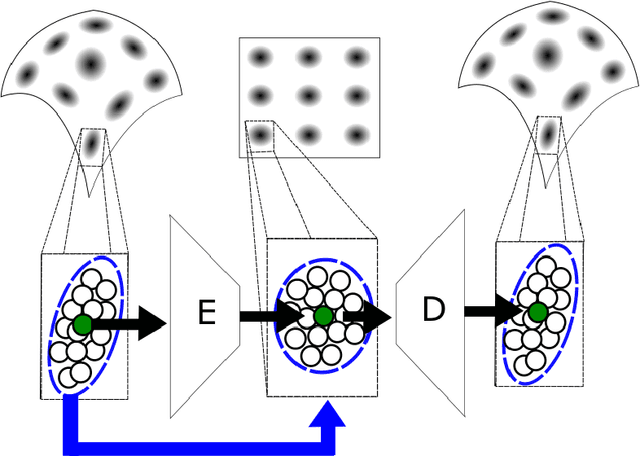
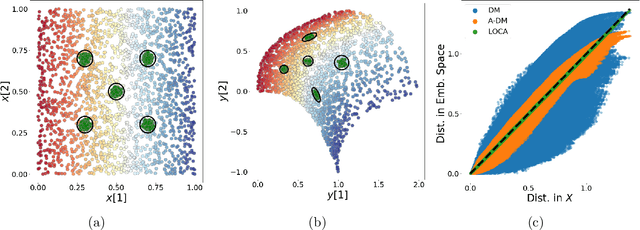
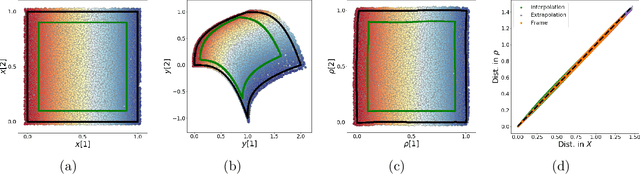
We propose a deep-learning based method for obtaining standardized data coordinates from scientific measurements.Data observations are modeled as samples from an unknown, non-linear deformation of an underlying Riemannian manifold, which is parametrized by a few normalized latent variables. By leveraging a repeated measurement sampling strategy, we present a method for learning an embedding in $\mathbb{R}^d$ that is isometric to the latent variables of the manifold. These data coordinates, being invariant under smooth changes of variables, enable matching between different instrumental observations of the same phenomenon. Our embedding is obtained using a LOcal Conformal Autoencoder (LOCA), an algorithm that constructs an embedding to rectify deformations by using a local z-scoring procedure while preserving relevant geometric information. We demonstrate the isometric embedding properties of LOCA on various model settings and observe that it exhibits promising interpolation and extrapolation capabilities. Finally, we apply LOCA to single-site Wi-Fi localization data, and to $3$-dimensional curved surface estimation based on a $2$-dimensional projection.

Co-manifold learning with missing data

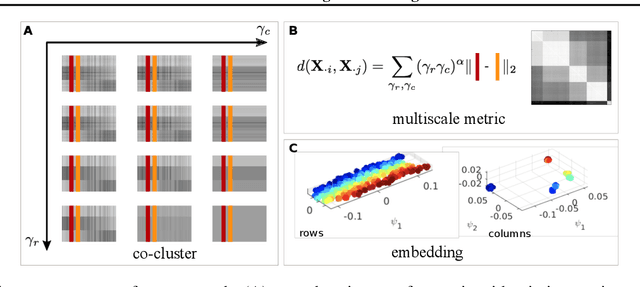
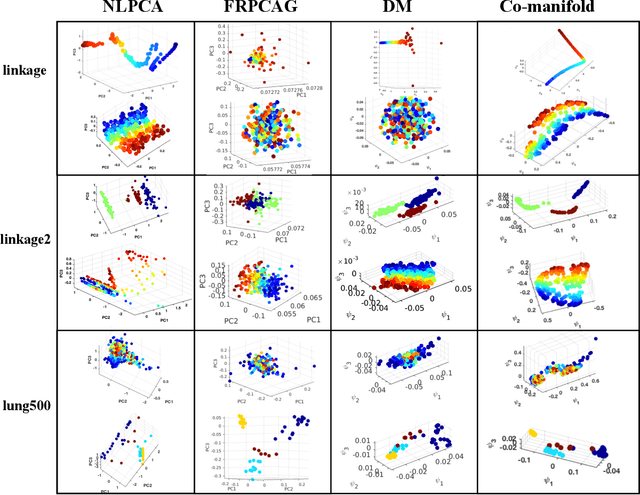
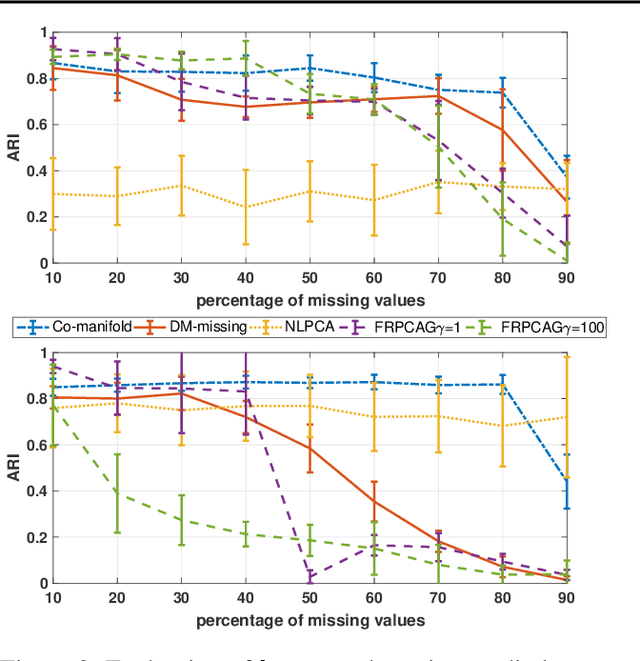
Representation learning is typically applied to only one mode of a data matrix, either its rows or columns. Yet in many applications, there is an underlying geometry to both the rows and the columns. We propose utilizing this coupled structure to perform co-manifold learning: uncovering the underlying geometry of both the rows and the columns of a given matrix, where we focus on a missing data setting. Our unsupervised approach consists of three components. We first solve a family of optimization problems to estimate a complete matrix at multiple scales of smoothness. We then use this collection of smooth matrix estimates to compute pairwise distances on the rows and columns based on a new multi-scale metric that implicitly introduces a coupling between the rows and the columns. Finally, we construct row and column representations from these multi-scale metrics. We demonstrate that our approach outperforms competing methods in both data visualization and clustering.

Two-sample Statistics Based on Anisotropic Kernels

The paper introduces a new kernel-based Maximum Mean Discrepancy (MMD) statistic for measuring the distance between two distributions given finitely-many multivariate samples. When the distributions are locally low-dimensional, the proposed test can be made more powerful to distinguish certain alternatives by incorporating local covariance matrices and constructing an anisotropic kernel. The kernel matrix is asymmetric; it computes the affinity between $n$ data points and a set of $n_R$ reference points, where $n_R$ can be drastically smaller than $n$. While the proposed statistic can be viewed as a special class of Reproducing Kernel Hilbert Space MMD, the consistency of the test is proved, under mild assumptions of the kernel, as long as $\|p-q\| \sqrt{n} \to \infty $, and a finite-sample lower bound of the testing power is obtained. Applications to flow cytometry and diffusion MRI datasets are demonstrated, which motivate the proposed approach to compare distributions.

Manifold learning with bi-stochastic kernels

In this paper we answer the following question: what is the infinitesimal generator of the diffusion process defined by a kernel that is normalized such that it is bi-stochastic with respect to a specified measure? More precisely, under the assumption that data is sampled from a Riemannian manifold we determine how the resulting infinitesimal generator depends on the potentially nonuniform distribution of the sample points, and the specified measure for the bi-stochastic normalization. In a special case, we demonstrate a connection to the heat kernel. We consider both the case where only a single data set is given, and the case where a data set and a reference set are given. The spectral theory of the constructed operators is studied, and Nystr\"om extension formulas for the gradients of the eigenfunctions are computed. Applications to discrete point sets and manifold learning are discussed.