Image denoising as a conditional expectation

All techniques for denoising involve a notion of a true (noise-free) image, and a hypothesis space. The hypothesis space may reconstruct the image directly as a grayscale valued function, or indirectly by its Fourier or wavelet spectrum. Most common techniques estimate the true image as a projection to some subspace. We propose an interpretation of a noisy image as a collection of samples drawn from a certain probability space. Within this interpretation, projection based approaches are not guaranteed to be unbiased and convergent. We present a data-driven denoising method in which the true image is recovered as a conditional expectation. Although the probability space is unknown apriori, integrals on this space can be estimated by kernel integral operators. The true image is reformulated as the least squares solution to a linear equation in a reproducing kernel Hilbert space (RKHS), and involving various kernel integral operators as linear transforms. Assuming the true image to be a continuous function on a compact planar domain, the technique is shown to be convergent as the number of pixels goes to infinity. We also show that for a picture with finite number of pixels, the convergence result can be used to choose the various parameters for an optimum denoising result.

Conditional expectation using compactification operators

The separate tasks of denoising, conditional expectation and manifold learning can often be posed in a common setting of finding the conditional expectations arising from a product of two random variables. This paper focuses on this more general problem and describes an operator theoretic approach to estimating the conditional expectation. Kernel integral operators are used as a compactification tool, to set up the estimation problem as a linear inverse problem in a reproducing kernel Hilbert space. This equation is shown to have solutions that are stable to numerical approximation, thus guaranteeing the convergence of data-driven implementations. The overall technique is easy to implement, and their successful application to some real-world problems are also shown.

An information-geometric approach to feature extraction and moment reconstruction in dynamical systems

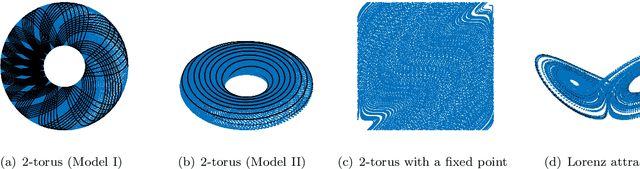
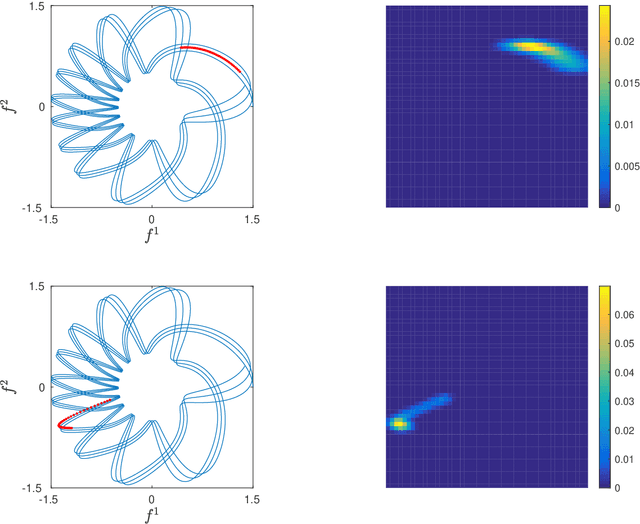
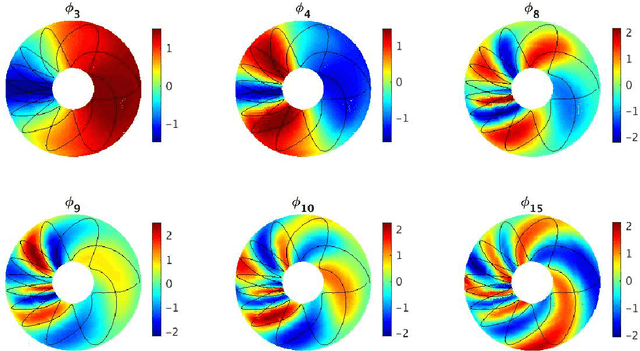
We propose a dimension reduction framework for feature extraction and moment reconstruction in dynamical systems that operates on spaces of probability measures induced by observables of the system rather than directly in the original data space of the observables themselves as in more conventional methods. Our approach is based on the fact that orbits of a dynamical system induce probability measures over the measurable space defined by (partial) observations of the system. We equip the space of these probability measures with a divergence, i.e., a distance between probability distributions, and use this divergence to define a kernel integral operator. The eigenfunctions of this operator create an orthonormal basis of functions that capture different timescales of the dynamical system. One of our main results shows that the evolution of the moments of the dynamics-dependent probability measures can be related to a time-averaging operator on the original dynamical system. Using this result, we show that the moments can be expanded in the eigenfunction basis, thus opening up the avenue for nonparametric forecasting of the moments. If the collection of probability measures is itself a manifold, we can in addition equip the statistical manifold with the Riemannian metric and use techniques from information geometry. We present applications to ergodic dynamical systems on the 2-torus and the Lorenz 63 system, and show on a real-world example that a small number of eigenvectors is sufficient to reconstruct the moments (here the first four moments) of an atmospheric time series, i.e., the realtime multivariate Madden-Julian oscillation index.