Transferred Q-learning

We consider $Q$-learning with knowledge transfer, using samples from a target reinforcement learning (RL) task as well as source samples from different but related RL tasks. We propose transfer learning algorithms for both batch and online $Q$-learning with offline source studies. The proposed transferred $Q$-learning algorithm contains a novel re-targeting step that enables vertical information-cascading along multiple steps in an RL task, besides the usual horizontal information-gathering as transfer learning (TL) for supervised learning. We establish the first theoretical justifications of TL in RL tasks by showing a faster rate of convergence of the $Q$ function estimation in the offline RL transfer, and a lower regret bound in the offline-to-online RL transfer under certain similarity assumptions. Empirical evidences from both synthetic and real datasets are presented to back up the proposed algorithm and our theoretical results.

Reinforcement Learning with Heterogeneous Data: Estimation and Inference

Reinforcement Learning (RL) has the promise of providing data-driven support for decision-making in a wide range of problems in healthcare, education, business, and other domains. Classical RL methods focus on the mean of the total return and, thus, may provide misleading results in the setting of the heterogeneous populations that commonly underlie large-scale datasets. We introduce the K-Heterogeneous Markov Decision Process (K-Hetero MDP) to address sequential decision problems with population heterogeneity. We propose the Auto-Clustered Policy Evaluation (ACPE) for estimating the value of a given policy, and the Auto-Clustered Policy Iteration (ACPI) for estimating the optimal policy in a given policy class. Our auto-clustered algorithms can automatically detect and identify homogeneous sub-populations, while estimating the Q function and the optimal policy for each sub-population. We establish convergence rates and construct confidence intervals for the estimators obtained by the ACPE and ACPI. We present simulations to support our theoretical findings, and we conduct an empirical study on the standard MIMIC-III dataset. The latter analysis shows evidence of value heterogeneity and confirms the advantages of our new method.

On Projection Robust Optimal Transport: Sample Complexity and Model Misspecification

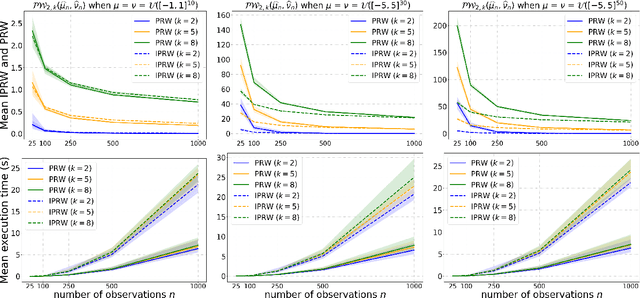
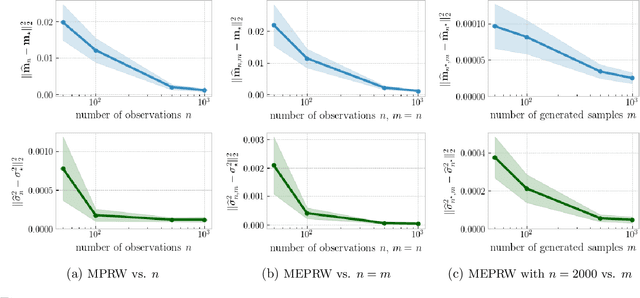
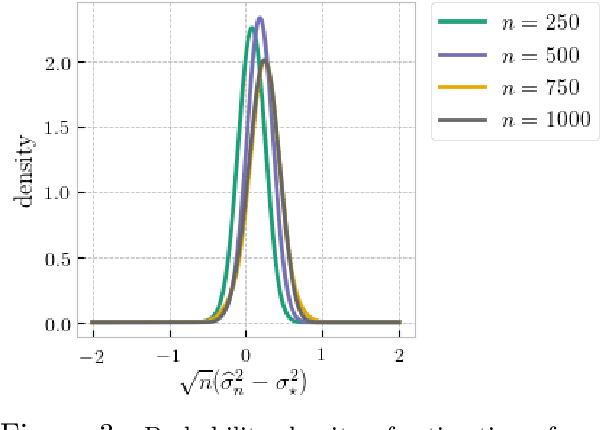
Optimal transport (OT) distances are increasingly used as loss functions for statistical inference, notably in the learning of generative models or supervised learning. Yet, the behavior of minimum Wasserstein estimators is poorly understood, notably in high-dimensional regimes or under model misspecification. In this work we adopt the viewpoint of projection robust (PR) OT, which seeks to maximize the OT cost between two measures by choosing a $k$-dimensional subspace onto which they can be projected. Our first contribution is to establish several fundamental statistical properties of PR Wasserstein distances, complementing and improving previous literature that has been restricted to one-dimensional and well-specified cases. Next, we propose the integral PR Wasserstein (IPRW) distance as an alternative to the PRW distance, by averaging rather than optimizing on subspaces. Our complexity bounds can help explain why both PRW and IPRW distances outperform Wasserstein distances empirically in high-dimensional inference tasks. Finally, we consider parametric inference using the PRW distance. We provide an asymptotic guarantee of two types of minimum PRW estimators and formulate a central limit theorem for max-sliced Wasserstein estimator under model misspecification. To enable our analysis on PRW with projection dimension larger than one, we devise a novel combination of variational analysis and statistical theory.

Low-Rank Principal Eigenmatrix Analysis

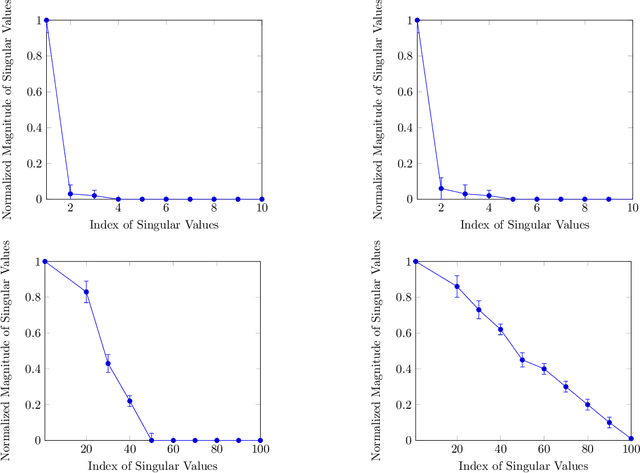
Sparse PCA is a widely used technique for high-dimensional data analysis. In this paper, we propose a new method called low-rank principal eigenmatrix analysis. Different from sparse PCA, the dominant eigenvectors are allowed to be dense but are assumed to have a low-rank structure when matricized appropriately. Such a structure arises naturally in several practical cases: Indeed the top eigenvector of a circulant matrix, when matricized appropriately is a rank-1 matrix. We propose a matricized rank-truncated power method that could be efficiently implemented and establish its computational and statistical properties. Extensive experiments on several synthetic data sets demonstrate the competitive empirical performance of our method.