GIMLET: Generalizable and Interpretable Model Learning through Embedded Thermodynamics

We develop a data-driven framework for discovering constitutive relations in models of fluid flow and scalar transport. Our approach infers unknown closure terms in the governing equations (gray-box discovery) under the assumption that the temporal derivative, convective transport, and pressure-gradient contributions are known. The formulation is rooted in a variational principle from nonequilibrium thermodynamics, where the dynamics is defined by a free-energy functional and a dissipation functional. The unknown constitutive terms arise as functional derivatives of these functionals with respect to the state variables. To enable a flexible and structured model discovery, the free-energy and dissipation functionals are parameterized using neural networks, while their functional derivatives are obtained via automatic differentiation. This construction enforces thermodynamic consistency by design, ensuring monotonic decay of the total free energy and non-negative entropy production. The resulting method, termed GIMLET (Generalizable and Interpretable Model Learning through Embedded Thermodynamics), avoids reliance on a predefined library of candidate functions, unlike sparse regression or symbolic identification approaches. The learned models are generalizable in that functionals identified from one dataset can be transferred to distinct datasets governed by the same underlying equations. Moreover, the inferred free-energy and dissipation functions provide direct physical interpretability of the learned dynamics. The framework is demonstrated on several benchmark systems, including the viscous Burgers equation, the Kuramoto--Sivashinsky equation, and the incompressible Navier--Stokes equations for both Newtonian and non-Newtonian fluids.

Probabilistic Predictions of Process-Induced Deformation in Carbon/Epoxy Composites Using a Deep Operator Network

Fiber reinforcement and polymer matrix respond differently to manufacturing conditions due to mismatch in coefficient of thermal expansion and matrix shrinkage during curing of thermosets. These heterogeneities generate residual stresses over multiple length scales, whose partial release leads to process-induced deformation (PID), requiring accurate prediction and mitigation via optimized non-isothermal cure cycles. This study considers a unidirectional AS4 carbon fiber/amine bi-functional epoxy prepreg and models PID using a two-mechanism framework that accounts for thermal expansion/shrinkage and cure shrinkage. The model is validated against manufacturing trials to identify initial and boundary conditions, then used to generate PID responses for a diverse set of non-isothermal cure cycles (time-temperature profiles). Building on this physics-based foundation, we develop a data-driven surrogate based on Deep Operator Networks (DeepONets). A DeepONet is trained on a dataset combining high-fidelity simulations with targeted experimental measurements of PID. We extend this to a Feature-wise Linear Modulation (FiLM) DeepONet, where branch-network features are modulated by external parameters, including the initial degree of cure, enabling prediction of time histories of degree of cure, viscosity, and deformation. Because experimental data are available only at limited time instances (for example, final deformation), we use transfer learning: simulation-trained trunk and branch networks are fixed and only the final layer is updated using measured final deformation. Finally, we augment the framework with Ensemble Kalman Inversion (EKI) to quantify uncertainty under experimental conditions and to support optimization of cure schedules for reduced PID in composites.

Characterization of partial wetting by CMAS droplets using multiphase many-body dissipative particle dynamics and data-driven discovery based on PINNs

The molten sand, a mixture of calcia, magnesia, alumina, and silicate, known as CMAS, is characterized by its high viscosity, density, and surface tension. The unique properties of CMAS make it a challenging material to deal with in high-temperature applications, requiring innovative solutions and materials to prevent its buildup and damage to critical equipment. Here, we use multiphase many-body dissipative particle dynamics (mDPD) simulations to study the wetting dynamics of highly viscous molten CMAS droplets. The simulations are performed in three dimensions, with varying initial droplet sizes and equilibrium contact angles. We propose a coarse parametric ordinary differential equation (ODE) that captures the spreading radius behavior of the CMAS droplets. The ODE parameters are then identified based on the Physics-Informed Neural Network (PINN) framework. Subsequently, the closed form dependency of parameter values found by PINN on the initial radii and contact angles are given using symbolic regression. Finally, we employ Bayesian PINNs (B-PINNs) to assess and quantify the uncertainty associated with the discovered parameters. In brief, this study provides insight into spreading dynamics of CMAS droplets by fusing simple parametric ODE modeling and state-of-the-art machine learning techniques.

A Framework Based on Symbolic Regression Coupled with eXtended Physics-Informed Neural Networks for Gray-Box Learning of Equations of Motion from Data

We propose a framework and an algorithm to uncover the unknown parts of nonlinear equations directly from data. The framework is based on eXtended Physics-Informed Neural Networks (X-PINNs), domain decomposition in space-time, but we augment the original X-PINN method by imposing flux continuity across the domain interfaces. The well-known Allen-Cahn equation is used to demonstrate the approach. The Frobenius matrix norm is used to evaluate the accuracy of the X-PINN predictions and the results show excellent performance. In addition, symbolic regression is employed to determine the closed form of the unknown part of the equation from the data, and the results confirm the accuracy of the X-PINNs based approach. To test the framework in a situation resembling real-world data, random noise is added to the datasets to mimic scenarios such as the presence of thermal noise or instrument errors. The results show that the framework is stable against significant amount of noise. As the final part, we determine the minimal amount of data required for training the neural network. The framework is able to predict the correct form and coefficients of the underlying dynamical equation when at least 50\% data is used for training.

Machine Learning-Driven Process of Alumina Ceramics Laser Machining

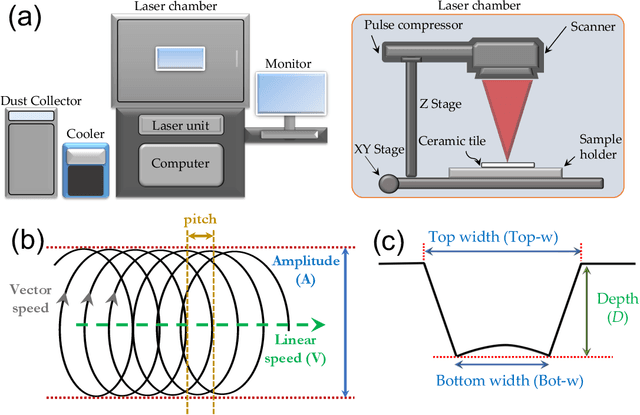
Laser machining is a highly flexible non-contact manufacturing technique that has been employed widely across academia and industry. Due to nonlinear interactions between light and matter, simulation methods are extremely crucial, as they help enhance the machining quality by offering comprehension of the inter-relationships between the laser processing parameters. On the other hand, experimental processing parameter optimization recommends a systematic, and consequently time-consuming, investigation over the available processing parameter space. An intelligent strategy is to employ machine learning (ML) techniques to capture the relationship between picosecond laser machining parameters for finding proper parameter combinations to create the desired cuts on industrial-grade alumina ceramic with deep, smooth and defect-free patterns. Laser parameters such as beam amplitude and frequency, scanner passing speed and the number of passes over the surface, as well as the vertical distance of the scanner from the sample surface, are used for predicting the depth, top width, and bottom width of the engraved channels using ML models. Owing to the complex correlation between laser parameters, it is shown that Neural Networks (NN) are the most efficient in predicting the outputs. Equipped with an ML model that captures the interconnection between laser parameters and the engraved channel dimensions, one can predict the required input parameters to achieve a target channel geometry. This strategy significantly reduces the cost and effort of experimental laser machining during the development phase, without compromising accuracy or performance. The developed techniques can be applied to a wide range of ceramic laser machining processes.