Edward Schmerling
Perception-Aware Motion Planning via Multiobjective Search on GPUs
Dec 06, 2017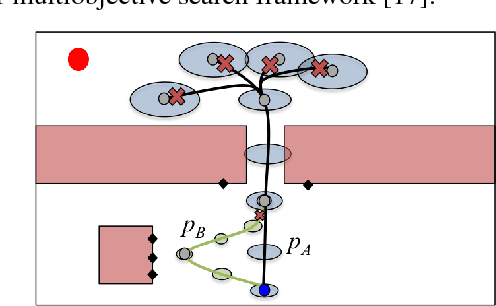
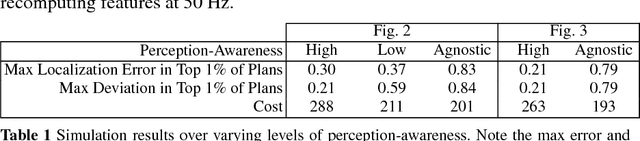
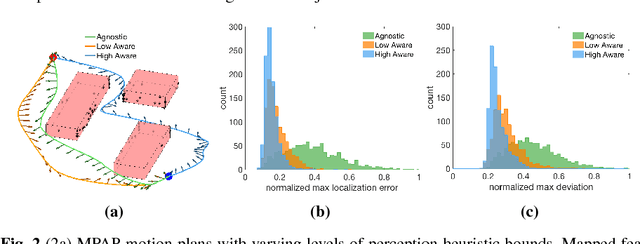
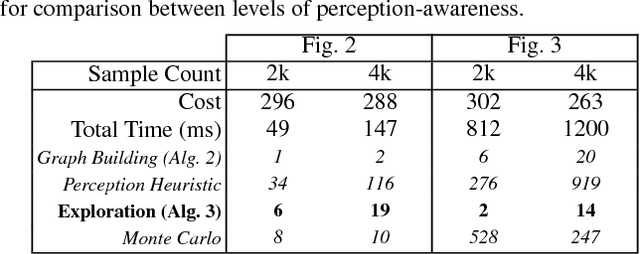
Abstract:In this paper we describe a framework towards computing well-localized, robust motion plans through the perception-aware motion planning problem, whereby we seek a low-cost motion plan subject to a separate constraint on perception localization quality. To solve this problem we introduce the Multiobjective Perception-Aware Planning (MPAP) algorithm which explores the state space via a multiobjective search, considering both cost and a perception heuristic. This framework can accommodate a large range of heuristics, allowing those that capture the history dependence of localization drift and represent complex modern perception methods. We present two such heuristics, one derived from a simplified model of robot perception and a second learned from ground-truth sensor error, which we show to be capable of predicting the performance of a state-of-the-art perception system. The solution trajectory from this heuristic-based search is then certified via Monte Carlo methods to be well-localized and robust. The additional computational burden of perception-aware planning is offset by GPU massive parallelization. Through numerical experiments the algorithm is shown to find well-localized, robust solutions in about a second. Finally, we demonstrate MPAP on a quadrotor flying perception-aware and perception-agnostic plans using Google Tango for localization, finding the quadrotor safely executes the perception-aware plan every time, while crashing in over 20% of the perception-agnostic runs due to loss of localization.
Multimodal Probabilistic Model-Based Planning for Human-Robot Interaction
Oct 25, 2017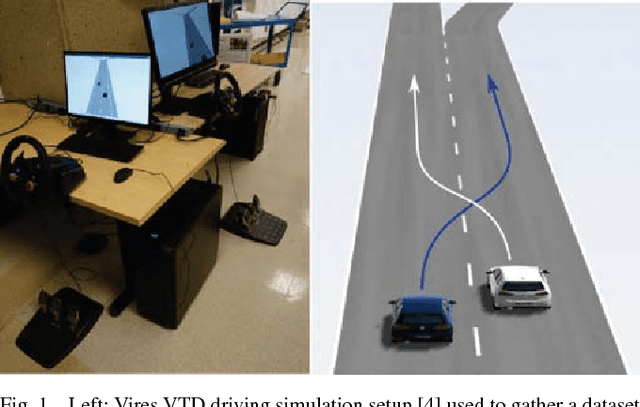
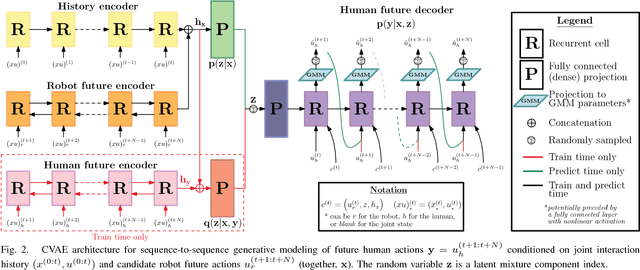
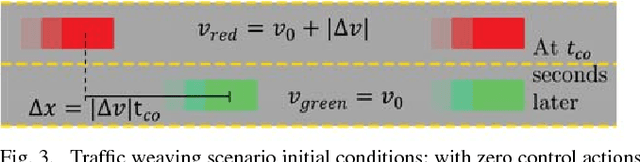
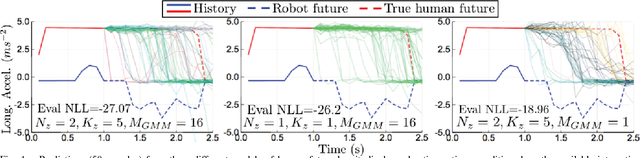
Abstract:This paper presents a method for constructing human-robot interaction policies in settings where multimodality, i.e., the possibility of multiple highly distinct futures, plays a critical role in decision making. We are motivated in this work by the example of traffic weaving, e.g., at highway on-ramps/off-ramps, where entering and exiting cars must swap lanes in a short distance---a challenging negotiation even for experienced drivers due to the inherent multimodal uncertainty of who will pass whom. Our approach is to learn multimodal probability distributions over future human actions from a dataset of human-human exemplars and perform real-time robot policy construction in the resulting environment model through massively parallel sampling of human responses to candidate robot action sequences. Direct learning of these distributions is made possible by recent advances in the theory of conditional variational autoencoders (CVAEs), whereby we learn action distributions simultaneously conditioned on the present interaction history, as well as candidate future robot actions in order to take into account response dynamics. We demonstrate the efficacy of this approach with a human-in-the-loop simulation of a traffic weaving scenario.
Evaluating Trajectory Collision Probability through Adaptive Importance Sampling for Safe Motion Planning
Jun 01, 2017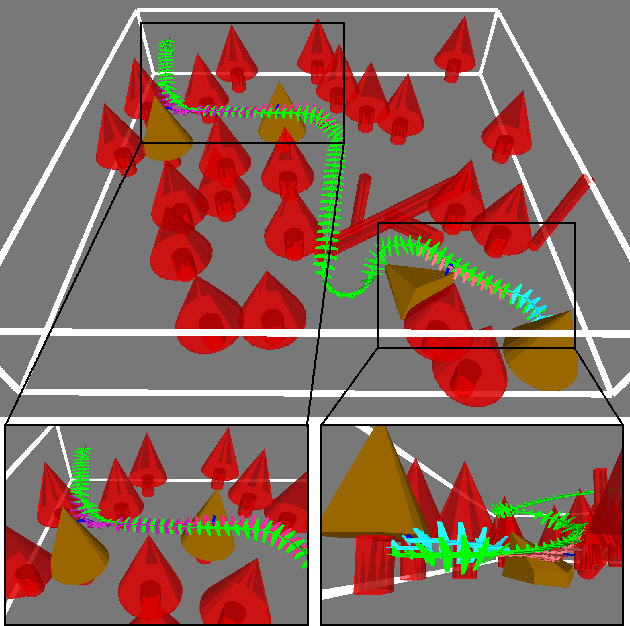
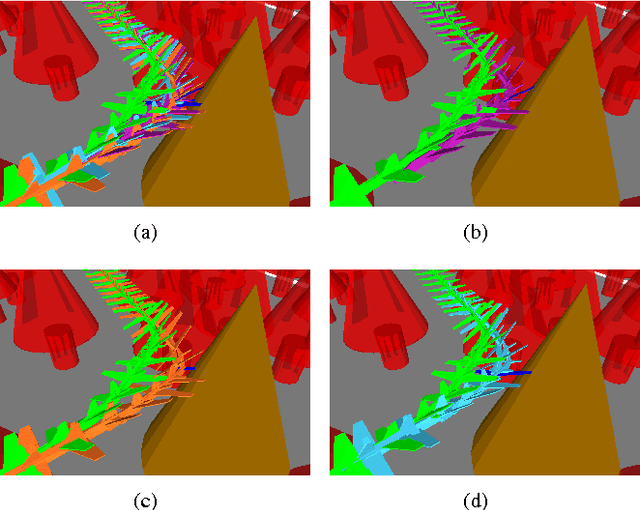
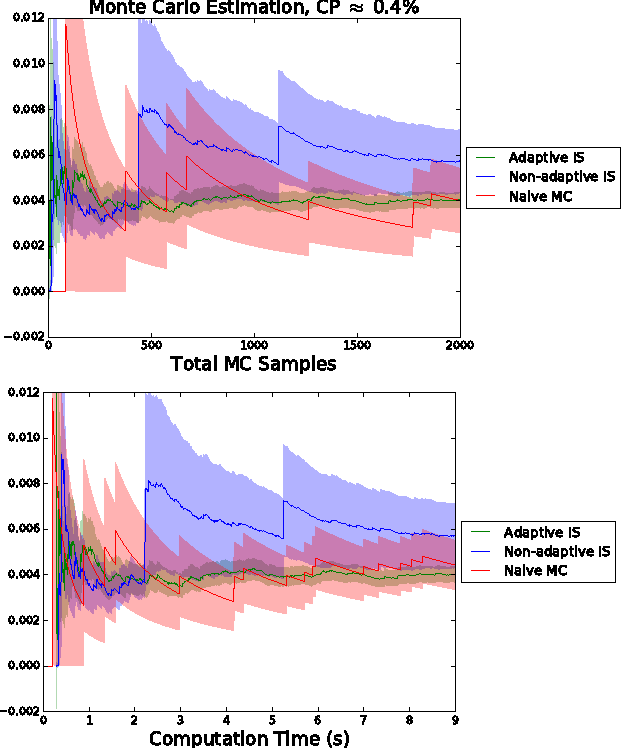

Abstract:This paper presents a tool for addressing a key component in many algorithms for planning robot trajectories under uncertainty: evaluation of the safety of a robot whose actions are governed by a closed-loop feedback policy near a nominal planned trajectory. We describe an adaptive importance sampling Monte Carlo framework that enables the evaluation of a given control policy for satisfaction of a probabilistic collision avoidance constraint which also provides an associated certificate of accuracy (in the form of a confidence interval). In particular this adaptive technique is well-suited to addressing the complexities of rigid-body collision checking applied to non-linear robot dynamics. As a Monte Carlo method it is amenable to parallelization for computational tractability, and is generally applicable to a wide gamut of simulatable systems, including alternative noise models. Numerical experiments demonstrating the effectiveness of the adaptive importance sampling procedure are presented and discussed.
Group Marching Tree: Sampling-Based Approximately Optimal Motion Planning on GPUs
May 05, 2017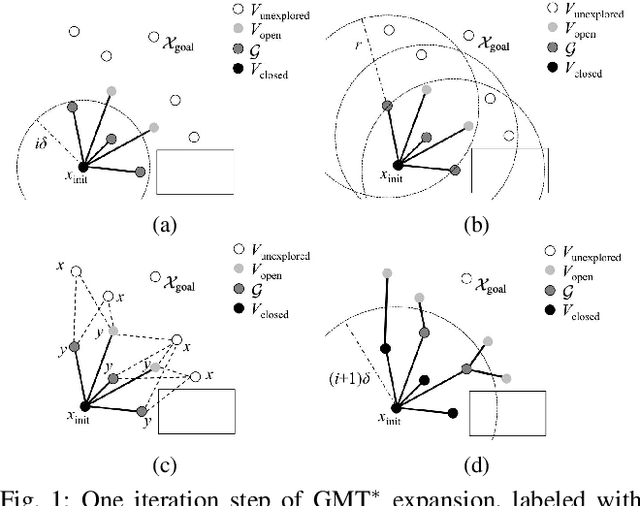
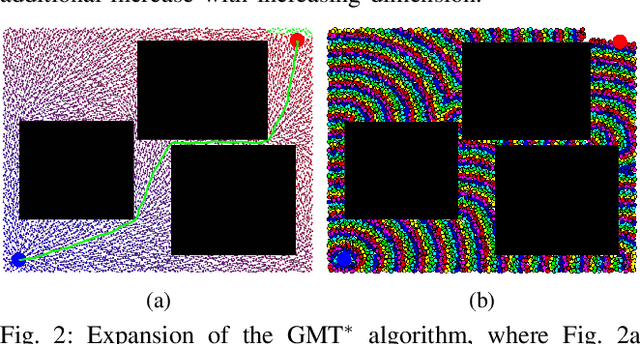
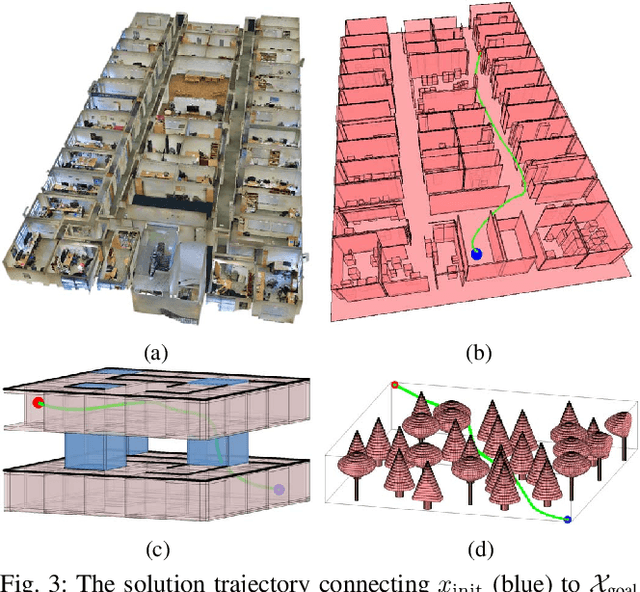
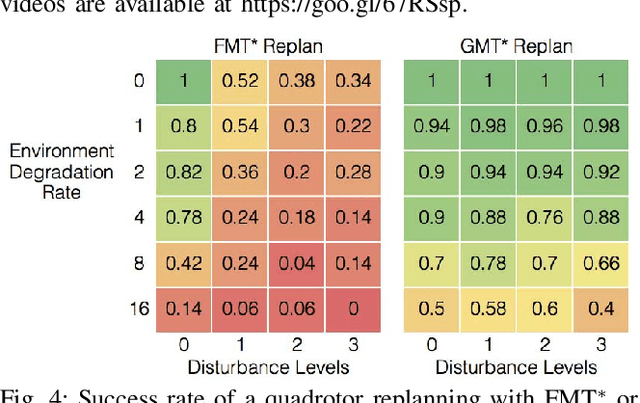
Abstract:This paper presents a novel approach, named the Group Marching Tree (GMT*) algorithm, to planning on GPUs at rates amenable to application within control loops, allowing planning in real-world settings via repeated computation of near-optimal plans. GMT*, like the Fast Marching Tree (FMT) algorithm, explores the state space with a "lazy" dynamic programming recursion on a set of samples to grow a tree of near-optimal paths. GMT*, however, alters the approach of FMT with approximate dynamic programming by expanding, in parallel, the group of all active samples with cost below an increasing threshold, rather than only the minimum cost sample. This group approximation enables low-level parallelism over the sample set and removes the need for sequential data structures, while the "lazy" collision checking limits thread divergence---all contributing to a very efficient GPU implementation. While this approach incurs some suboptimality, we prove that GMT* remains asymptotically optimal up to a constant multiplicative factor. We show solutions for complex planning problems under differential constraints can be found in ~10 ms on a desktop GPU and ~30 ms on an embedded GPU, representing a significant speed up over the state of the art, with only small losses in performance. Finally, we present a scenario demonstrating the efficacy of planning within the control loop (~100 Hz) towards operating in dynamic, uncertain settings.
Real-Time Stochastic Kinodynamic Motion Planning via Multiobjective Search on GPUs
Feb 23, 2017
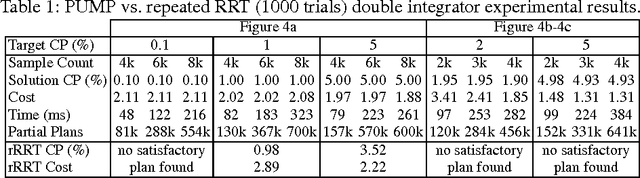
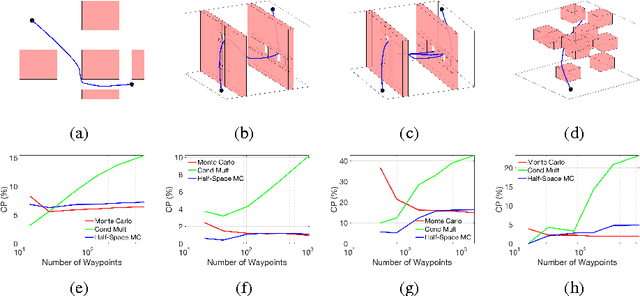
Abstract:In this paper we present the PUMP (Parallel Uncertainty-aware Multiobjective Planning) algorithm for addressing the stochastic kinodynamic motion planning problem, whereby one seeks a low-cost, dynamically-feasible motion plan subject to a constraint on collision probability (CP). To ensure exhaustive evaluation of candidate motion plans (as needed to tradeoff the competing objectives of performance and safety), PUMP incrementally builds the Pareto front of the problem, accounting for the optimization objective and an approximation of CP. This is performed by a massively parallel multiobjective search, here implemented with a focus on GPUs. Upon termination of the exploration phase, PUMP searches the Pareto set of motion plans to identify the lowest cost solution that is certified to satisfy the CP constraint (according to an asymptotically exact estimator). We introduce a novel particle-based CP approximation scheme, designed for efficient GPU implementation, which accounts for dependencies over the history of a trajectory execution. We present numerical experiments for quadrotor planning wherein PUMP identifies solutions in ~100 ms, evaluating over one hundred thousand partial plans through the course of its exploration phase. The results show that this multiobjective search achieves a lower motion plan cost, for the same CP constraint, compared to a safety buffer-based search heuristic and repeated RRT trials.
Decentralized Algorithms for 3D Symmetric Formations in Robotic Networks: a Contraction Theory Approach
Nov 09, 2015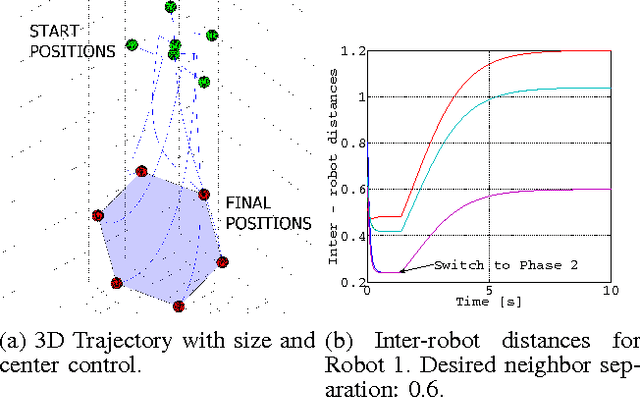
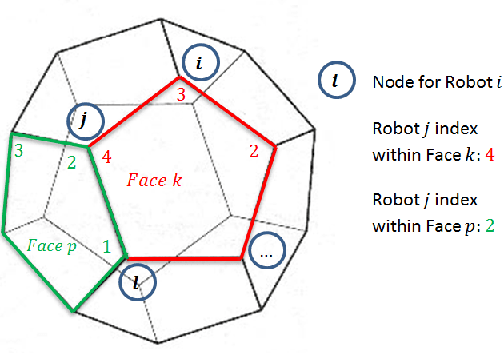
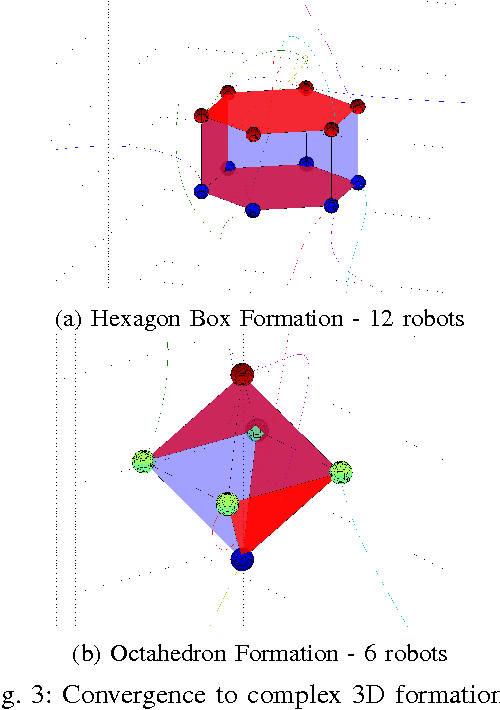
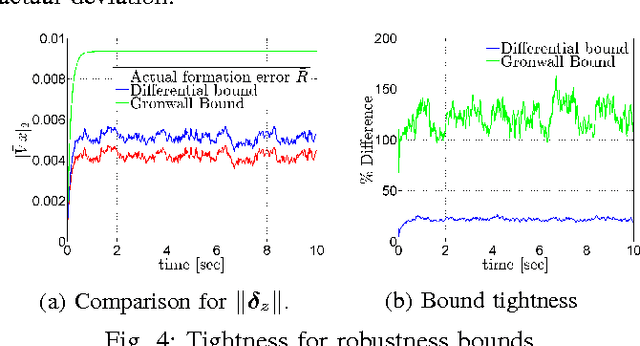
Abstract:This paper presents decentralized algorithms for formation control of multiple robots in three dimensions. Specifically, we leverage the mathematical properties of cyclic pursuit along with results from contraction and partial contraction theory to design decentralized control algorithms that ensure global convergence to symmetric formations. We first consider regular polygon formations as a base case, and then extend the results to Johnson solid and other polygonal mesh formations. The algorithms are further augmented to allow control over formation size and avoid collisions with other robots in the formation. The robustness properties of the algorithms are assessed in the presence of bounded additive disturbances and their effect on the quality of the formation is quantified. Finally, we present a general methodology for embedding the control laws on complex dynamical systems, in this case, quadcopters, and validate this approach via simulations and experiments on a fleet of quadcopters.
A Convex Optimization Approach to Smooth Trajectories for Motion Planning with Car-Like Robots
Oct 26, 2015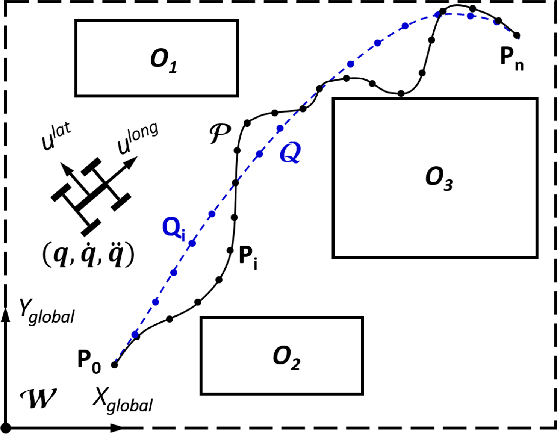
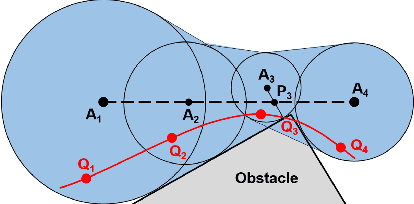
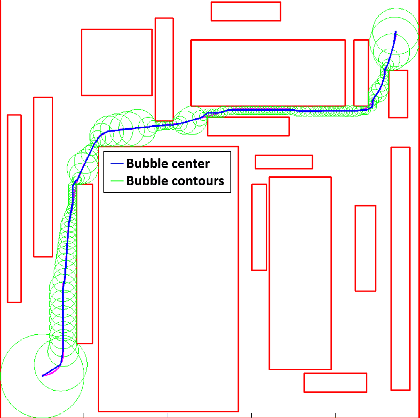
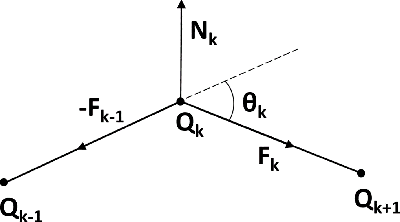
Abstract:In the recent past, several sampling-based algorithms have been proposed to compute trajectories that are collision-free and dynamically-feasible. However, the outputs of such algorithms are notoriously jagged. In this paper, by focusing on robots with car-like dynamics, we present a fast and simple heuristic algorithm, named Convex Elastic Smoothing (CES) algorithm, for trajectory smoothing and speed optimization. The CES algorithm is inspired by earlier work on elastic band planning and iteratively performs shape and speed optimization. The key feature of the algorithm is that both optimization problems can be solved via convex programming, making CES particularly fast. A range of numerical experiments show that the CES algorithm returns high-quality solutions in a matter of a few hundreds of milliseconds and hence appears amenable to a real-time implementation.
Optimal Sampling-Based Motion Planning under Differential Constraints: the Drift Case with Linear Affine Dynamics
Oct 26, 2015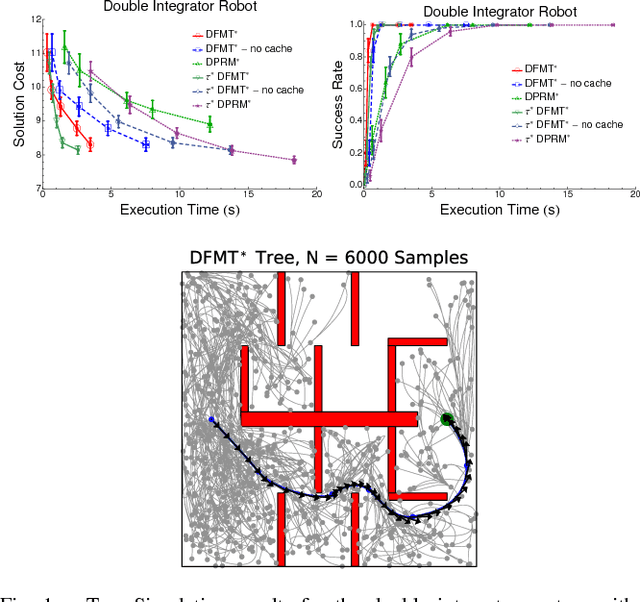
Abstract:In this paper we provide a thorough, rigorous theoretical framework to assess optimality guarantees of sampling-based algorithms for drift control systems: systems that, loosely speaking, can not stop instantaneously due to momentum. We exploit this framework to design and analyze a sampling-based algorithm (the Differential Fast Marching Tree algorithm) that is asymptotically optimal, that is, it is guaranteed to converge, as the number of samples increases, to an optimal solution. In addition, our approach allows us to provide concrete bounds on the rate of this convergence. The focus of this paper is on mixed time/control energy cost functions and on linear affine dynamical systems, which encompass a range of models of interest to applications (e.g., double-integrators) and represent a necessary step to design, via successive linearization, sampling-based and provably-correct algorithms for non-linear drift control systems. Our analysis relies on an original perturbation analysis for two-point boundary value problems, which could be of independent interest.
An Asymptotically-Optimal Sampling-Based Algorithm for Bi-directional Motion Planning
Jul 27, 2015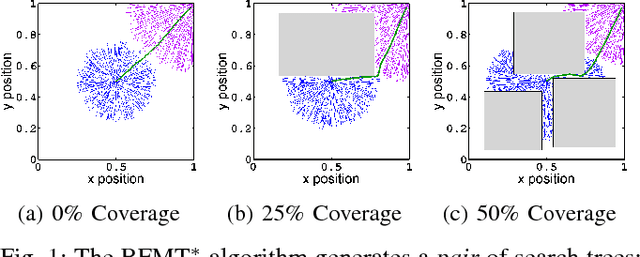
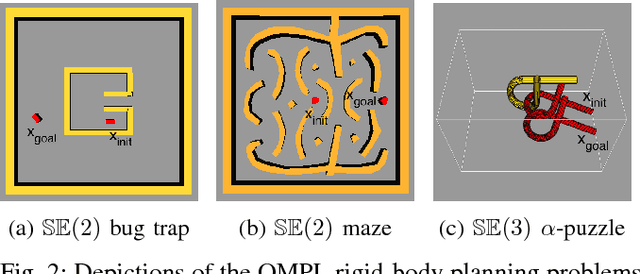
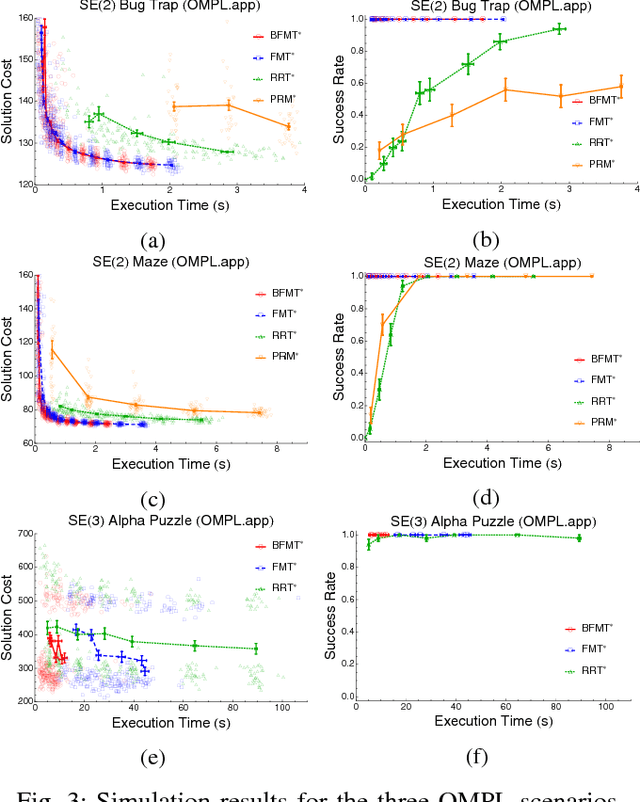
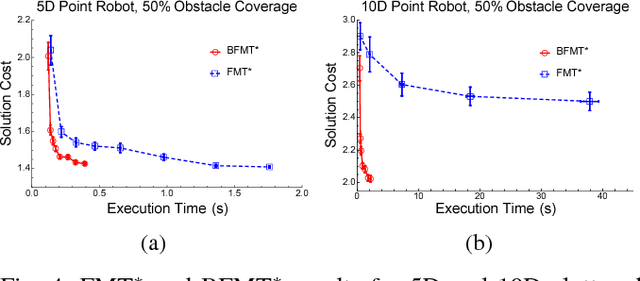
Abstract:Bi-directional search is a widely used strategy to increase the success and convergence rates of sampling-based motion planning algorithms. Yet, few results are available that merge both bi-directional search and asymptotic optimality into existing optimal planners, such as PRM*, RRT*, and FMT*. The objective of this paper is to fill this gap. Specifically, this paper presents a bi-directional, sampling-based, asymptotically-optimal algorithm named Bi-directional FMT* (BFMT*) that extends the Fast Marching Tree (FMT*) algorithm to bi-directional search while preserving its key properties, chiefly lazy search and asymptotic optimality through convergence in probability. BFMT* performs a two-source, lazy dynamic programming recursion over a set of randomly-drawn samples, correspondingly generating two search trees: one in cost-to-come space from the initial configuration and another in cost-to-go space from the goal configuration. Numerical experiments illustrate the advantages of BFMT* over its unidirectional counterpart, as well as a number of other state-of-the-art planners.
Monte Carlo Motion Planning for Robot Trajectory Optimization Under Uncertainty
May 29, 2015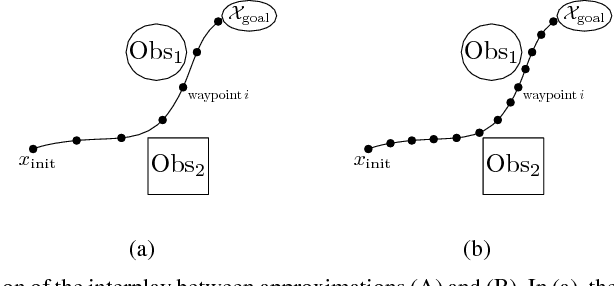
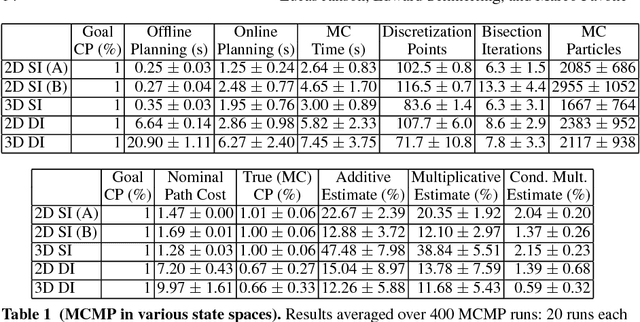
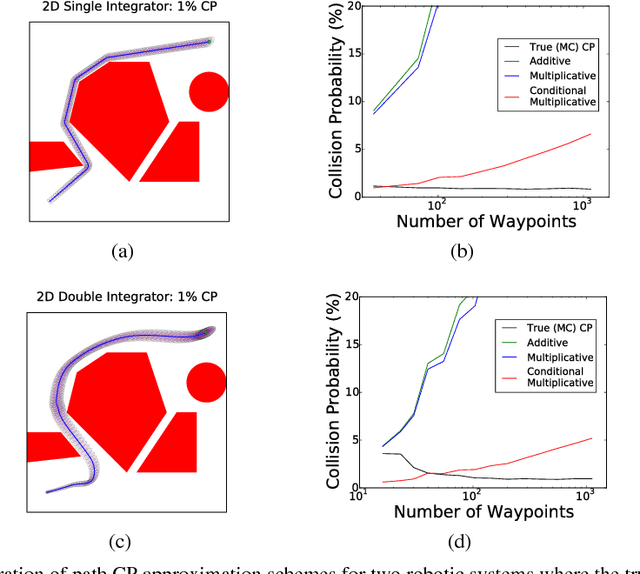
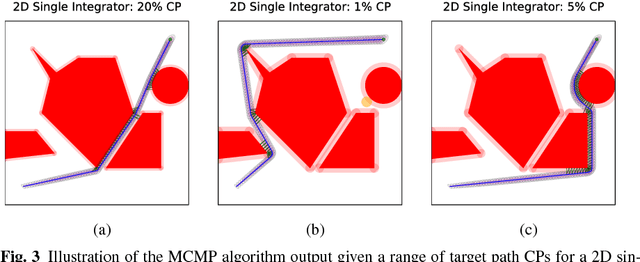
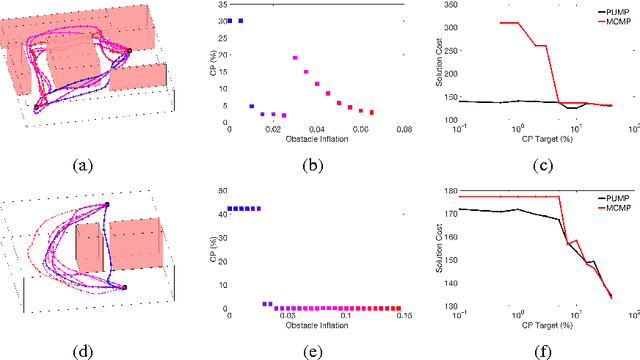
Abstract:This article presents a novel approach, named MCMP (Monte Carlo Motion Planning), to the problem of motion planning under uncertainty, i.e., to the problem of computing a low-cost path that fulfills probabilistic collision avoidance constraints. MCMP estimates the collision probability (CP) of a given path by sampling via Monte Carlo the execution of a reference tracking controller (in this paper we consider LQG). The key algorithmic contribution of this paper is the design of statistical variance-reduction techniques, namely control variates and importance sampling, to make such a sampling procedure amenable to real-time implementation. MCMP applies this CP estimation procedure to motion planning by iteratively (i) computing an (approximately) optimal path for the deterministic version of the problem (here, using the FMT* algorithm), (ii) computing the CP of this path, and (iii) inflating or deflating the obstacles by a common factor depending on whether the CP is higher or lower than a target value. The advantages of MCMP are threefold: (i) asymptotic correctness of CP estimation, as opposed to most current approximations, which, as shown in this paper, can be off by large multiples and hinder the computation of feasible plans; (ii) speed and parallelizability, and (iii) generality, i.e., the approach is applicable to virtually any planning problem provided that a path tracking controller and a notion of distance to obstacles in the configuration space are available. Numerical results illustrate the correctness (in terms of feasibility), efficiency (in terms of path cost), and computational speed of MCMP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge