Theano: A Python framework for fast computation of mathematical expressions

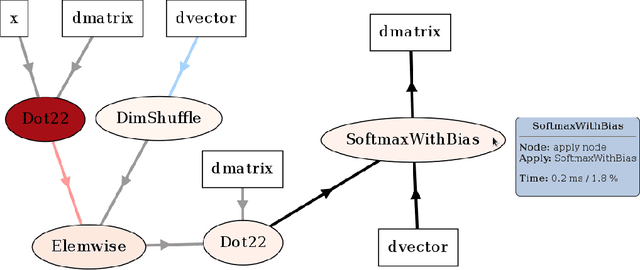
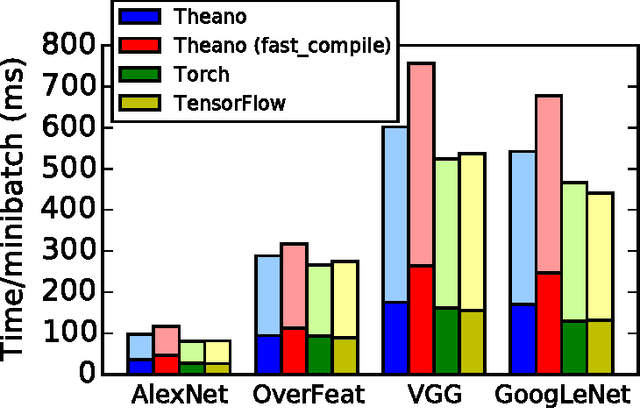
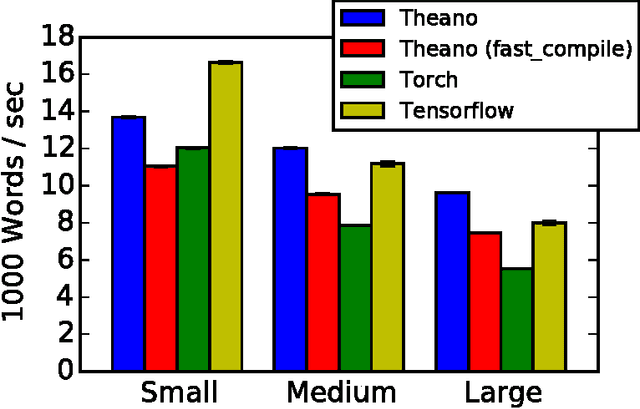
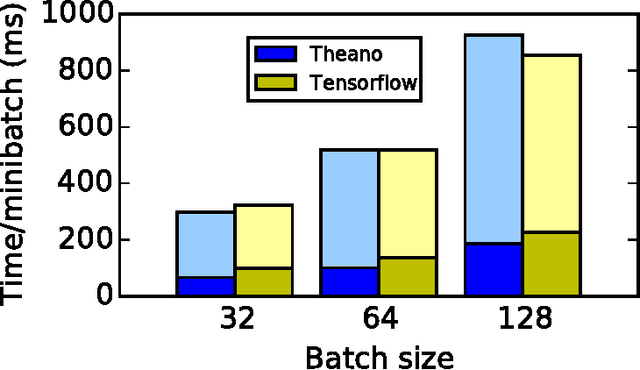
Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.

Kinodynamic RRT*: Optimal Motion Planning for Systems with Linear Differential Constraints

We present Kinodynamic RRT*, an incremental sampling-based approach for asymptotically optimal motion planning for robots with linear differential constraints. Our approach extends RRT*, which was introduced for holonomic robots (Karaman et al. 2011), by using a fixed-final-state-free-final-time controller that exactly and optimally connects any pair of states, where the cost function is expressed as a trade-off between the duration of a trajectory and the expended control effort. Our approach generalizes earlier work on extending RRT* to kinodynamic systems, as it guarantees asymptotic optimality for any system with controllable linear dynamics, in state spaces of any dimension. Our approach can be applied to non-linear dynamics as well by using their first-order Taylor approximations. In addition, we show that for the rich subclass of systems with a nilpotent dynamics matrix, closed-form solutions for optimal trajectories can be derived, which keeps the computational overhead of our algorithm compared to traditional RRT* at a minimum. We demonstrate the potential of our approach by computing asymptotically optimal trajectories in three challenging motion planning scenarios: (i) a planar robot with a 4-D state space and double integrator dynamics, (ii) an aerial vehicle with a 10-D state space and linearized quadrotor dynamics, and (iii) a car-like robot with a 5-D state space and non-linear dynamics.