A parametric framework for kernel-based dynamic mode decomposition using deep learning

Surrogate modelling is widely applied in computational science and engineering to mitigate computational efficiency issues for the real-time simulations of complex and large-scale computational models or for many-query scenarios, such as uncertainty quantification and design optimisation. In this work, we propose a parametric framework for kernel-based dynamic mode decomposition method based on the linear and nonlinear disambiguation optimization (LANDO) algorithm. The proposed parametric framework consists of two stages, offline and online. The offline stage prepares the essential component for prediction, namely a series of LANDO models that emulate the dynamics of the system with particular parameters from a training dataset. The online stage leverages those LANDO models to generate new data at a desired time instant, and approximate the mapping between parameters and the state with the data using deep learning techniques. Moreover, dimensionality reduction technique is applied to high-dimensional dynamical systems to reduce the computational cost of training. Three numerical examples including Lotka-Volterra model, heat equation and reaction-diffusion equation are presented to demonstrate the efficiency and effectiveness of the proposed framework.

Gaussian process learning of nonlinear dynamics

One of the pivotal tasks in scientific machine learning is to represent underlying dynamical systems from time series data. Many methods for such dynamics learning explicitly require the derivatives of state data, which are not directly available and can be approximated conventionally by finite differences. However, the discrete approximations of time derivatives may result in a poor estimation when state data are scarce and/or corrupted by noise, thus compromising the predictiveness of the learned dynamical models. To overcome this technical hurdle, we propose a new method that learns nonlinear dynamics through a Bayesian inference of characterizing model parameters. This method leverages a Gaussian process representation of states, and constructs a likelihood function using the correlation between state data and their derivatives, yet prevents explicit evaluations of time derivatives. Through a Bayesian scheme, a probabilistic estimate of the model parameters is given by the posterior distribution, and thus a quantification is facilitated for uncertainties from noisy state data and the learning process. Specifically, we will discuss the applicability of the proposed method to two typical scenarios for dynamical systems: parameter identification and estimation with an affine structure of the system, and nonlinear parametric approximation without prior knowledge.

Bayesian approach to Gaussian process regression with uncertain inputs

Conventional Gaussian process regression exclusively assumes the existence of noise in the output data of model observations. In many scientific and engineering applications, however, the input locations of observational data may also be compromised with uncertainties owing to modeling assumptions, measurement errors, etc. In this work, we propose a Bayesian method that integrates the variability of input data into Gaussian process regression. Considering two types of observables -- noise-corrupted outputs with fixed inputs and those with prior-distribution-defined uncertain inputs, a posterior distribution is estimated via a Bayesian framework to infer the uncertain data locations. Thereafter, such quantified uncertainties of inputs are incorporated into Gaussian process predictions by means of marginalization. The effectiveness of this new regression technique is demonstrated through several numerical examples, in which a consistently good performance of generalization is observed, while a substantial reduction in the predictive uncertainties is achieved by the Bayesian inference of uncertain inputs.

Data-driven reduced-order modelling for blood flow simulations with geometry-informed snapshots

Computational fluid dynamics is a common tool in cardiovascular science and engineering to simulate, predict and study hemodynamics in arteries. However, owing to the complexity and scale of cardiovascular flow problems, the evaluation of the model could be computationally expensive, especially in those cases where a large number of evaluations are required, such as uncertainty quantification and design optimisation. In such scenarios, the model may have to be repeatedly evaluated due to the changes or distinctions of simulation domains. In this work, a data-driven surrogate model is proposed for the efficient prediction of blood flow simulations on similar but distinct domains. The proposed surrogate model leverages surface registration to parameterise those similar but distinct shapes and formulate corresponding hemodynamics information into geometry-informed snapshots by the diffeomorphism constructed between the reference domain and target domain. A non-intrusive reduced-order model for geometrical parameters is subsequently constructed using proper orthogonal decomposition, and a radial basis function interpolator is trained for predicting the reduced coefficients of the reduced-order model based on reduced coefficients of geometrical parameters of the shape. Two examples of blood flowing through a stenosis and a bifurcation are presented and analysed. The proposed surrogate model demonstrates its accuracy and efficiency in hemodynamics prediction and shows its potential application toward real-time simulation or uncertainty quantification for complex patient-specific scenarios.

Uncertainty quantification of a 3D In-Stent Restenosis model with surrogate modelling

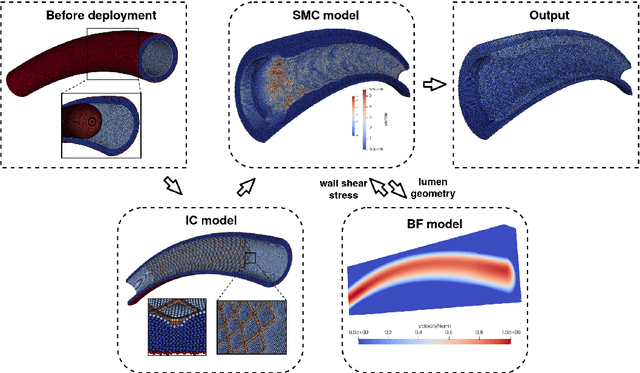
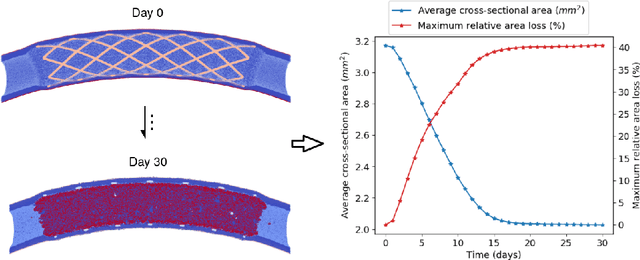
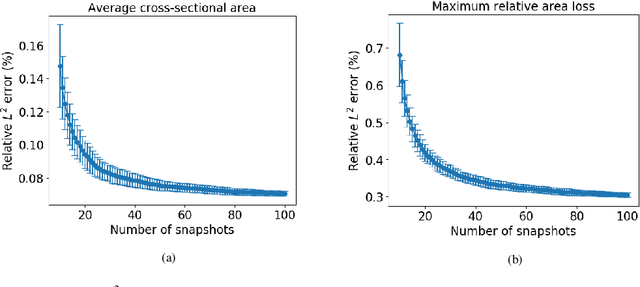
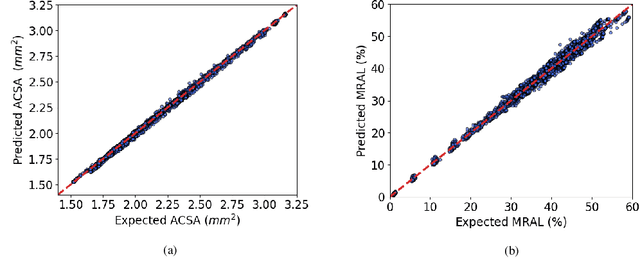
In-Stent Restenosis is a recurrence of coronary artery narrowing due to vascular injury caused by balloon dilation and stent placement. It may lead to the relapse of angina symptoms or to an acute coronary syndrome. An uncertainty quantification of a model for In-Stent Restenosis with four uncertain parameters (endothelium regeneration time, the threshold strain for smooth muscle cells bond breaking, blood flow velocity and the percentage of fenestration in the internal elastic lamina) is presented. Two quantities of interest were studied, namely the average cross-sectional area and the maximum relative area loss in a vessel. Due to the computational intensity of the model and the number of evaluations required in the uncertainty quantification, a surrogate model, based on Gaussian process regression with proper orthogonal decomposition, was developed which subsequently replaced the original In-Stent Restenosis model in the uncertainty quantification. A detailed analysis of the uncertainty propagation and sensitivity analysis is presented. Around 11% and 16% of uncertainty are observed on the average cross-sectional area and maximum relative area loss respectively, and the uncertainty estimates show that a higher fenestration mainly determines uncertainty in the neointimal growth at the initial stage of the process. On the other hand, the uncertainty in blood flow velocity and endothelium regeneration time mainly determine the uncertainty in the quantities of interest at the later, clinically relevant stages of the restenosis process. The uncertainty in the threshold strain is relatively small compared to the other uncertain parameters.