Dimitris Papailiopoulos
On the Utility of Gradient Compression in Distributed Training Systems
Mar 03, 2021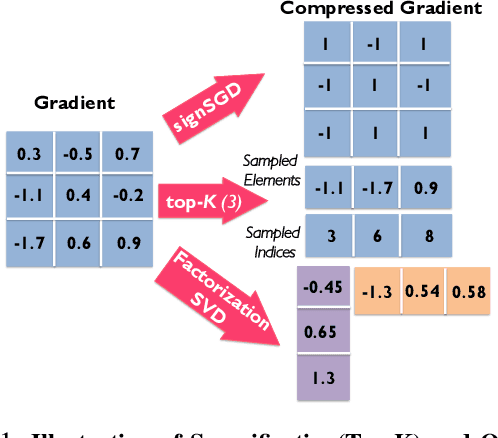


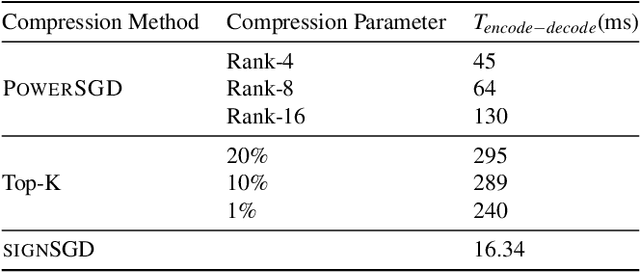
Abstract:Rapid growth in data sets and the scale of neural network architectures have rendered distributed training a necessity. A rich body of prior work has highlighted the existence of communication bottlenecks in synchronous data-parallel training. To alleviate these bottlenecks, the machine learning community has largely focused on developing gradient and model compression methods. In parallel, the systems community has adopted several High Performance Computing (HPC)techniques to speed up distributed training. In this work, we evaluate the efficacy of gradient compression methods and compare their scalability with optimized implementations of synchronous data-parallel SGD. Surprisingly, we observe that due to computation overheads introduced by gradient compression, the net speedup over vanilla data-parallel training is marginal, if not negative. We conduct an extensive investigation to identify the root causes of this phenomenon, and offer a performance model that can be used to identify the benefits of gradient compression for a variety of system setups. Based on our analysis, we propose a list of desirable properties that gradient compression methods should satisfy, in order for them to provide a meaningful end-to-end speedup
Permutation-Based SGD: Is Random Optimal?
Feb 19, 2021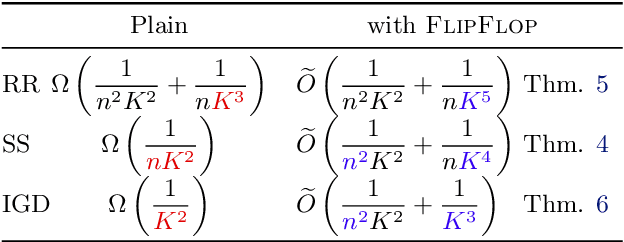
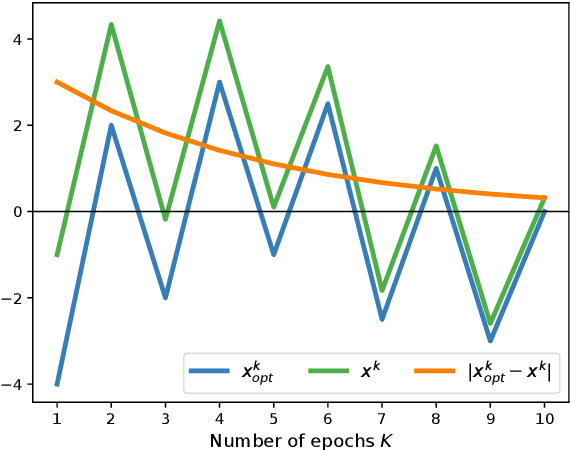
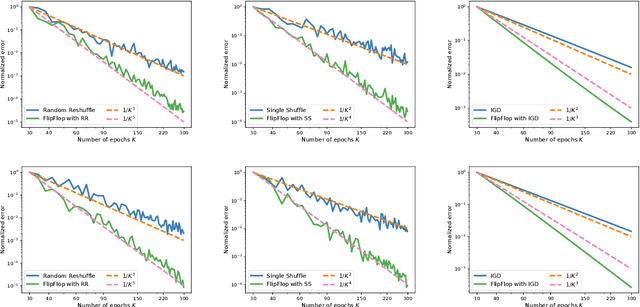
Abstract:A recent line of ground-breaking results for permutation-based SGD has corroborated a widely observed phenomenon: random permutations offer faster convergence than with-replacement sampling. However, is random optimal? We show that this depends heavily on what functions we are optimizing, and the convergence gap between optimal and random permutations can vary from exponential to nonexistent. We first show that for 1-dimensional strongly convex functions, with smooth second derivatives, there exist optimal permutations that offer exponentially faster convergence compared to random. However, for general strongly convex functions, random permutations are optimal. Finally, we show that for quadratic, strongly-convex functions, there are easy-to-construct permutations that lead to accelerated convergence compared to random. Our results suggest that a general convergence characterization of optimal permutations cannot capture the nuances of individual function classes, and can mistakenly indicate that one cannot do much better than random.
Accordion: Adaptive Gradient Communication via Critical Learning Regime Identification
Oct 29, 2020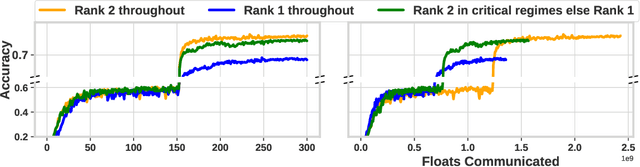
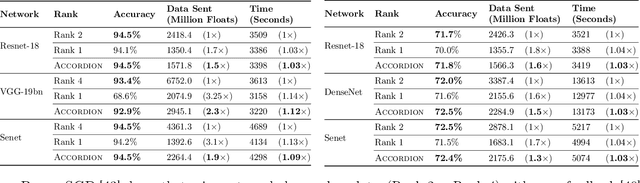
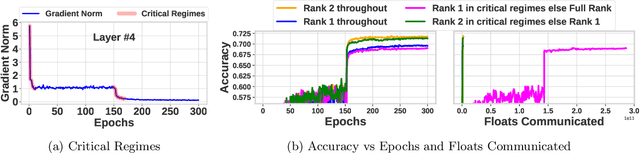
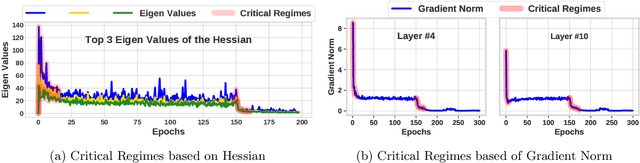
Abstract:Distributed model training suffers from communication bottlenecks due to frequent model updates transmitted across compute nodes. To alleviate these bottlenecks, practitioners use gradient compression techniques like sparsification, quantization, or low-rank updates. The techniques usually require choosing a static compression ratio, often requiring users to balance the trade-off between model accuracy and per-iteration speedup. In this work, we show that such performance degradation due to choosing a high compression ratio is not fundamental. An adaptive compression strategy can reduce communication while maintaining final test accuracy. Inspired by recent findings on critical learning regimes, in which small gradient errors can have irrecoverable impact on model performance, we propose Accordion a simple yet effective adaptive compression algorithm. While Accordion maintains a high enough compression rate on average, it avoids over-compressing gradients whenever in critical learning regimes, detected by a simple gradient-norm based criterion. Our extensive experimental study over a number of machine learning tasks in distributed environments indicates that Accordion, maintains similar model accuracy to uncompressed training, yet achieves up to 5.5x better compression and up to 4.1x end-to-end speedup over static approaches. We show that Accordion also works for adjusting the batch size, another popular strategy for alleviating communication bottlenecks.
Attack of the Tails: Yes, You Really Can Backdoor Federated Learning
Jul 09, 2020
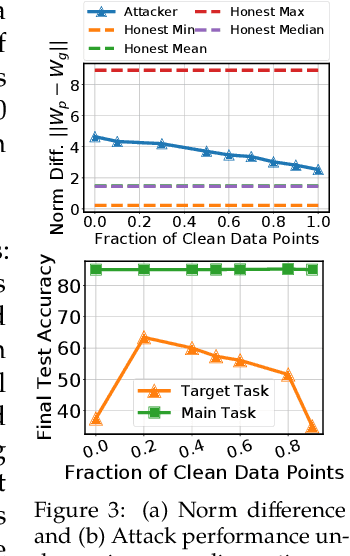
Abstract:Due to its decentralized nature, Federated Learning (FL) lends itself to adversarial attacks in the form of backdoors during training. The goal of a backdoor is to corrupt the performance of the trained model on specific sub-tasks (e.g., by classifying green cars as frogs). A range of FL backdoor attacks have been introduced in the literature, but also methods to defend against them, and it is currently an open question whether FL systems can be tailored to be robust against backdoors. In this work, we provide evidence to the contrary. We first establish that, in the general case, robustness to backdoors implies model robustness to adversarial examples, a major open problem in itself. Furthermore, detecting the presence of a backdoor in a FL model is unlikely assuming first order oracles or polynomial time. We couple our theoretical results with a new family of backdoor attacks, which we refer to as edge-case backdoors. An edge-case backdoor forces a model to misclassify on seemingly easy inputs that are however unlikely to be part of the training, or test data, i.e., they live on the tail of the input distribution. We explain how these edge-case backdoors can lead to unsavory failures and may have serious repercussions on fairness, and exhibit that with careful tuning at the side of the adversary, one can insert them across a range of machine learning tasks (e.g., image classification, OCR, text prediction, sentiment analysis).
Optimal Lottery Tickets via SubsetSum: Logarithmic Over-Parameterization is Sufficient
Jun 14, 2020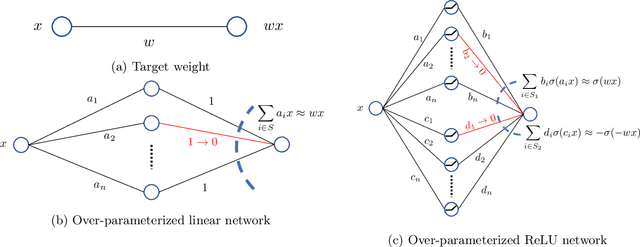
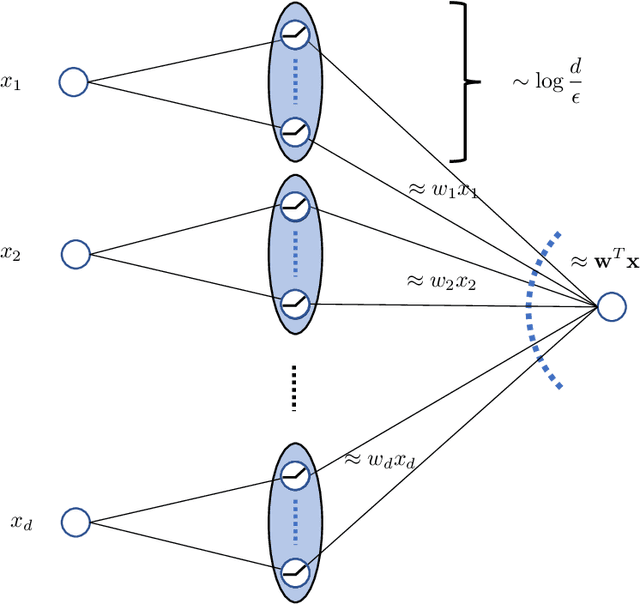
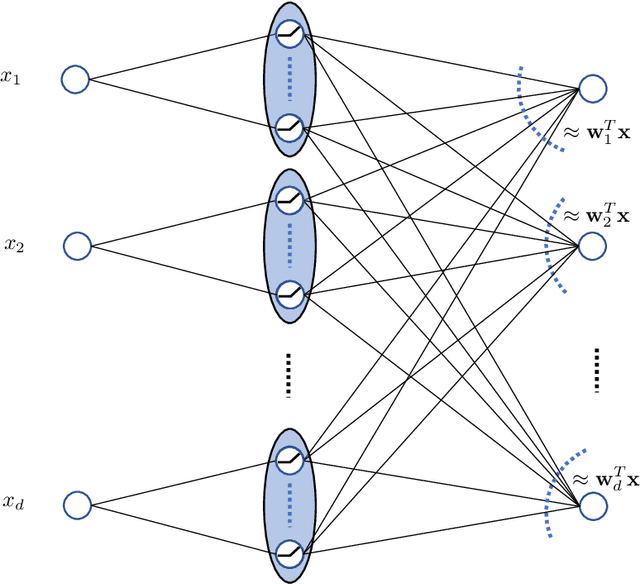
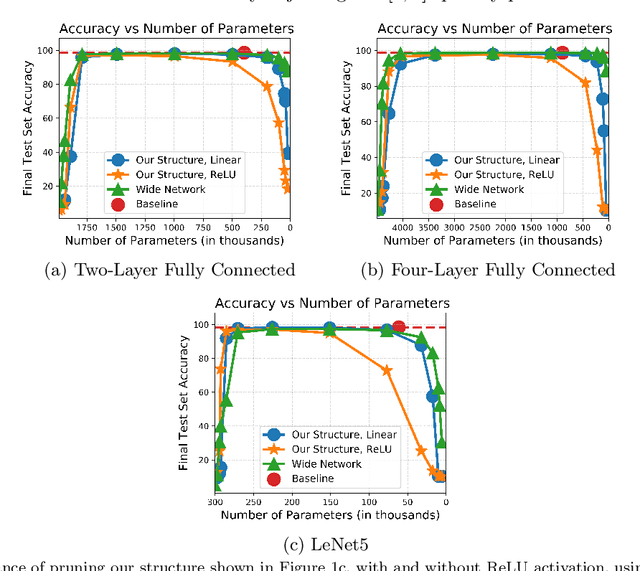
Abstract:The strong {\it lottery ticket hypothesis} (LTH) postulates that one can approximate any target neural network by only pruning the weights of a sufficiently over-parameterized random network. A recent work by Malach et al.~\cite{MalachEtAl20} establishes the first theoretical analysis for the strong LTH: one can provably approximate a neural network of width $d$ and depth $l$, by pruning a random one that is a factor $O(d^4l^2)$ wider and twice as deep. This polynomial over-parameterization requirement is at odds with recent experimental research that achieves good approximation with networks that are a small factor wider than the target. In this work, we close the gap and offer an exponential improvement to the over-parameterization requirement for the existence of lottery tickets. We show that any target network of width $d$ and depth $l$ can be approximated by pruning a random network that is a factor $O(\log(dl))$ wider and twice as deep. Our analysis heavily relies on connecting pruning random ReLU networks to random instances of the \textsc{SubsetSum} problem. We then show that this logarithmic over-parameterization is essentially optimal for constant depth networks. Finally, we verify several of our theoretical insights with experiments.
Closing the convergence gap of SGD without replacement
Mar 05, 2020
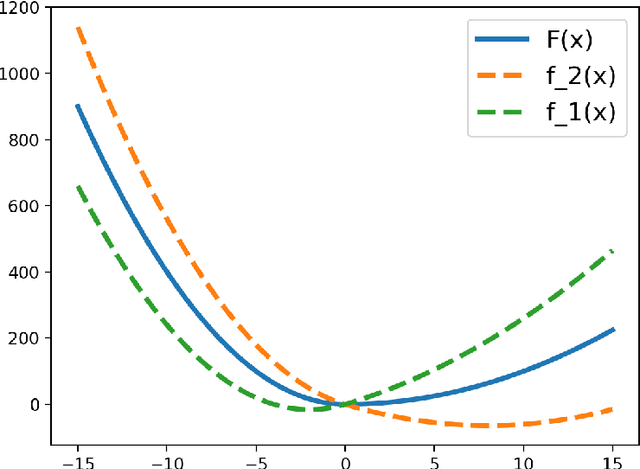
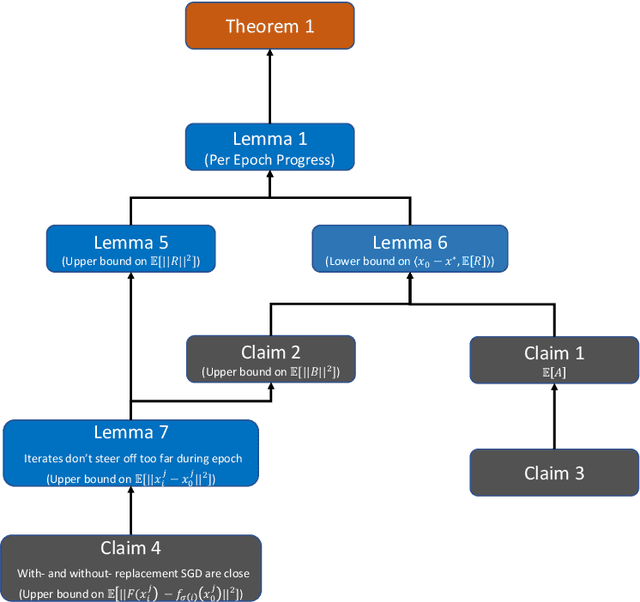
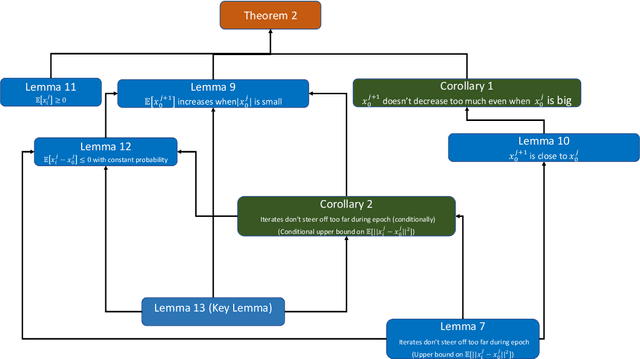
Abstract:Stochastic gradient descent without replacement sampling is widely used in practice for model training. However, the vast majority of SGD analyses assumes data sampled with replacement, and when the function minimized is strongly convex, an $\mathcal{O}\left(\frac{1}{T}\right)$ rate can be established when SGD is run for $T$ iterations. A recent line of breakthrough work on SGD without replacement (SGDo) established an $\mathcal{O}\left(\frac{n}{T^2}\right)$ convergence rate when the function minimized is strongly convex and is a sum of $n$ smooth functions, and an $\mathcal{O}\left(\frac{1}{T^2}+\frac{n^3}{T^3}\right)$ rate for sums of quadratics. On the other hand, the tightest known lower bound postulates an $\Omega\left(\frac{1}{T^2}+\frac{n^2}{T^3}\right)$ rate, leaving open the possibility of better SGDo convergence rates in the general case. In this paper, we close this gap and show that SGD without replacement achieves a rate of $\mathcal{O}\left(\frac{1}{T^2}+\frac{n^2}{T^3}\right)$ when the sum of the functions is a quadratic, and offer a new lower bound of $\Omega\left(\frac{n}{T^2}\right)$ for strongly convex functions that are sums of smooth functions.
Federated Learning with Matched Averaging
Feb 15, 2020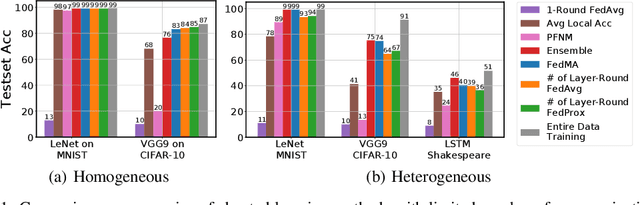

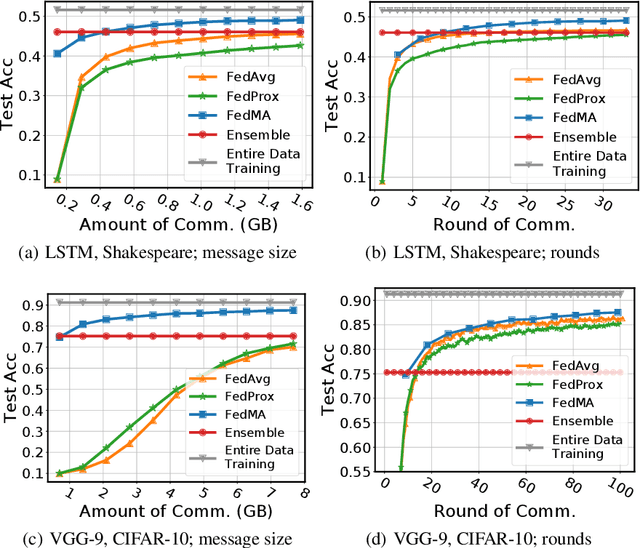

Abstract:Federated learning allows edge devices to collaboratively learn a shared model while keeping the training data on device, decoupling the ability to do model training from the need to store the data in the cloud. We propose Federated matched averaging (FedMA) algorithm designed for federated learning of modern neural network architectures e.g. convolutional neural networks (CNNs) and LSTMs. FedMA constructs the shared global model in a layer-wise manner by matching and averaging hidden elements (i.e. channels for convolution layers; hidden states for LSTM; neurons for fully connected layers) with similar feature extraction signatures. Our experiments indicate that FedMA not only outperforms popular state-of-the-art federated learning algorithms on deep CNN and LSTM architectures trained on real world datasets, but also reduces the overall communication burden.
DETOX: A Redundancy-based Framework for Faster and More Robust Gradient Aggregation
Jul 29, 2019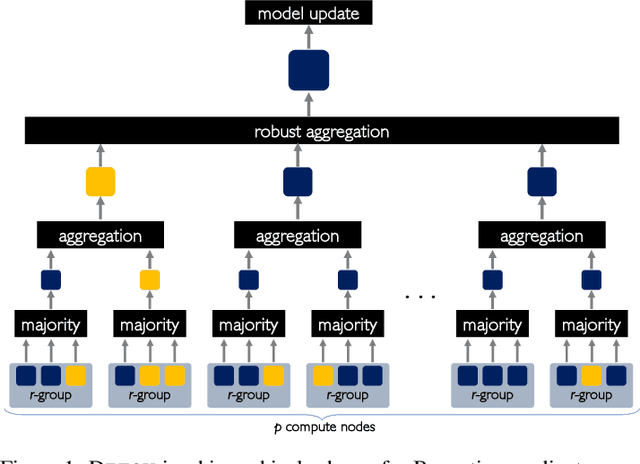
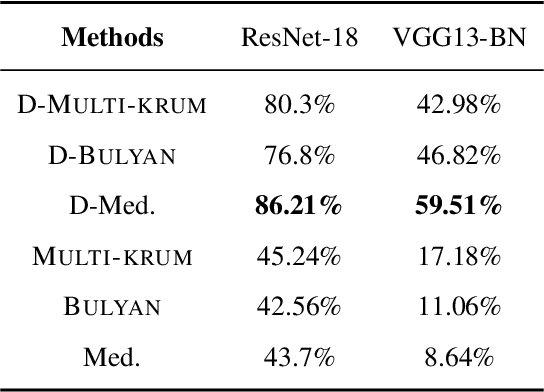

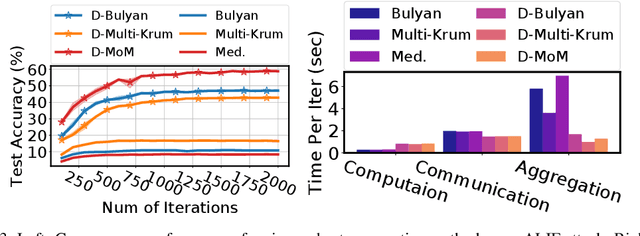
Abstract:To improve the resilience of distributed training to worst-case, or Byzantine node failures, several recent approaches have replaced gradient averaging with robust aggregation methods. Such techniques can have high computational costs, often quadratic in the number of compute nodes, and only have limited robustness guarantees. Other methods have instead used redundancy to guarantee robustness, but can only tolerate limited number of Byzantine failures. In this work, we present DETOX, a Byzantine-resilient distributed training framework that combines algorithmic redundancy with robust aggregation. DETOX operates in two steps, a filtering step that uses limited redundancy to significantly reduce the effect of Byzantine nodes, and a hierarchical aggregation step that can be used in tandem with any state-of-the-art robust aggregation method. We show theoretically that this leads to a substantial increase in robustness, and has a per iteration runtime that can be nearly linear in the number of compute nodes. We provide extensive experiments over real distributed setups across a variety of large-scale machine learning tasks, showing that DETOX leads to orders of magnitude accuracy and speedup improvements over many state-of-the-art Byzantine-resilient approaches.
Bad Global Minima Exist and SGD Can Reach Them
Jun 06, 2019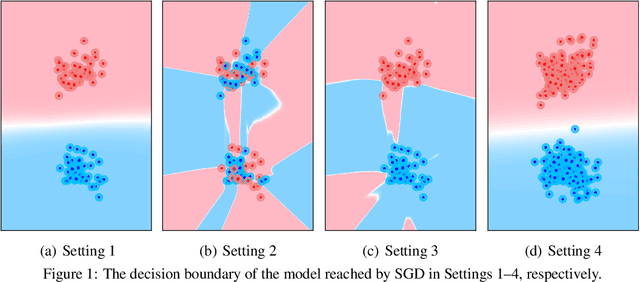
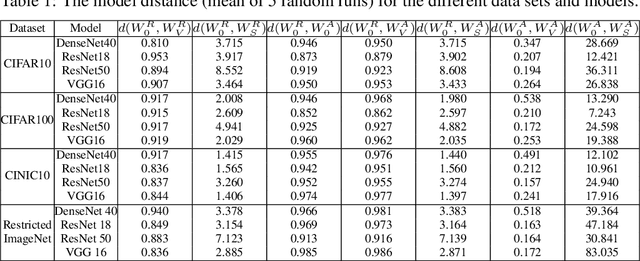
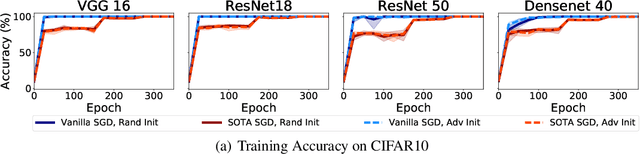
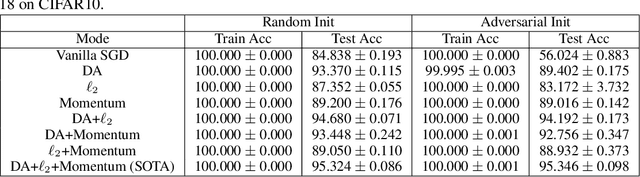
Abstract:Several recent works have aimed to explain why severely overparameterized models, generalize well when trained by Stochastic Gradient Descent (SGD). The emergent consensus explanation has two parts: the first is that there are "no bad local minima", while the second is that SGD performs implicit regularization by having a bias towards low complexity models. We revisit both of these ideas in the context of image classification with common deep neural network architectures. Our first finding is that there exist bad global minima, i.e., models that fit the training set perfectly, yet have poor generalization. Our second finding is that given only unlabeled training data, we can easily construct initializations that will cause SGD to quickly converge to such bad global minima. For example, on CIFAR, CINIC10, and (Restricted) ImageNet, this can be achieved by starting SGD at a model derived by fitting random labels on the training data: while subsequent SGD training (with the correct labels) will reach zero training error, the resulting model will exhibit a test accuracy degradation of up to 40% compared to training from a random initialization. Finally, we show that regularization seems to provide SGD with an escape route: once heuristics such as data augmentation are used, starting from a complex model (adversarial initialization) has no effect on the test accuracy.
Convergence and Margin of Adversarial Training on Separable Data
May 22, 2019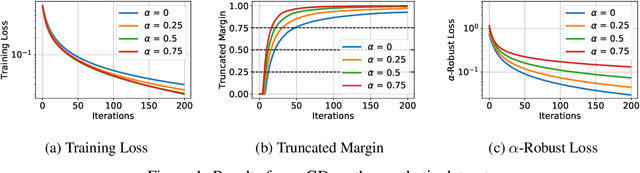
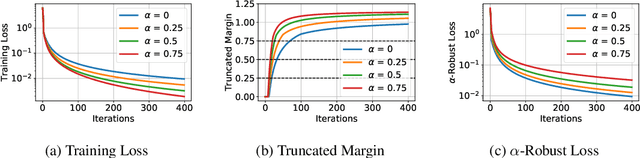
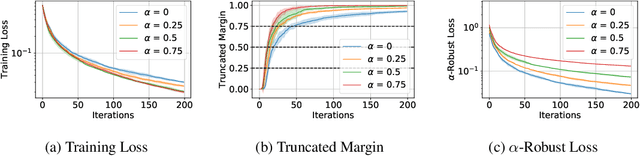
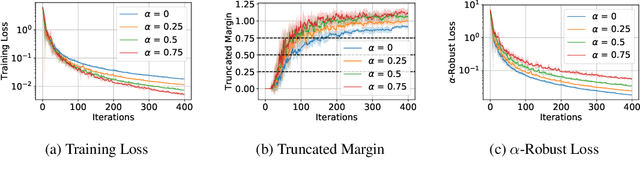
Abstract:Adversarial training is a technique for training robust machine learning models. To encourage robustness, it iteratively computes adversarial examples for the model, and then re-trains on these examples via some update rule. This work analyzes the performance of adversarial training on linearly separable data, and provides bounds on the number of iterations required for large margin. We show that when the update rule is given by an arbitrary empirical risk minimizer, adversarial training may require exponentially many iterations to obtain large margin. However, if gradient or stochastic gradient update rules are used, only polynomially many iterations are required to find a large-margin separator. By contrast, without the use of adversarial examples, gradient methods may require exponentially many iterations to achieve large margin. Our results are derived by showing that adversarial training with gradient updates minimizes a robust version of the empirical risk at a $\mathcal{O}(\ln(t)^2/t)$ rate, despite non-smoothness. We corroborate our theory empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge