Orthologics for Cones

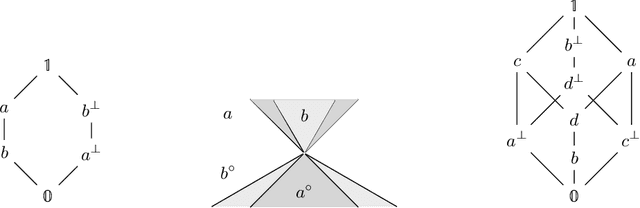
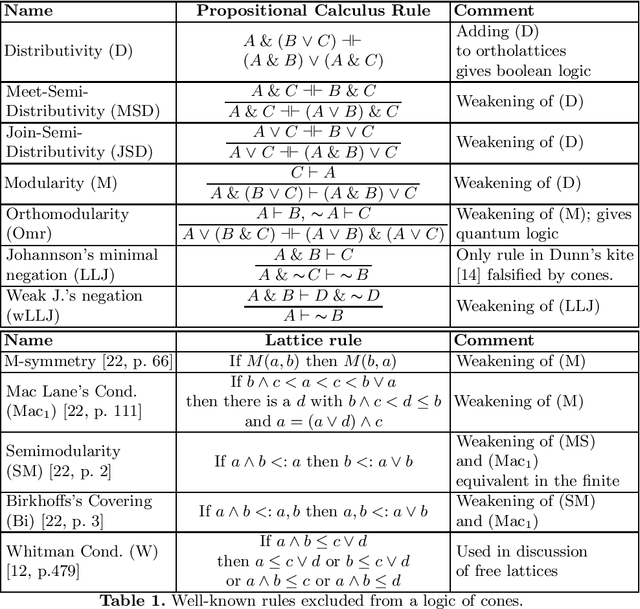
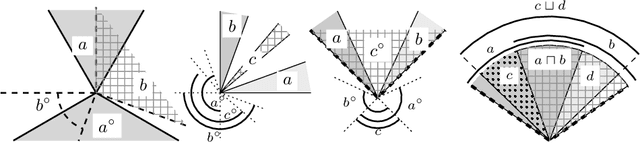
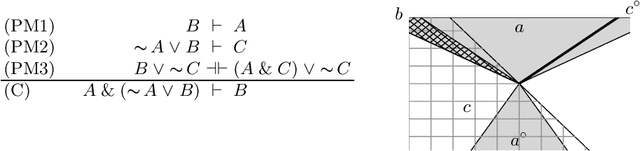
In applications that use knowledge representation (KR) techniques, in particular those that combine data-driven and logic methods, the domain of objects is not an abstract unstructured domain, but it exhibits a dedicated, deep structure of geometric objects. One example is the class of convex sets used to model natural concepts in conceptual spaces, which also links via convex optimization techniques to machine learning. In this paper we study logics for such geometric structures. Using the machinery of lattice theory, we describe an extension of minimal orthologic with a partial modularity rule that holds for closed convex cones. This logic combines a feasible data structure (exploiting convexity/conicity) with sufficient expressivity, including full orthonegation (exploiting conicity).

A Survey of Qualitative Spatial and Temporal Calculi -- Algebraic and Computational Properties

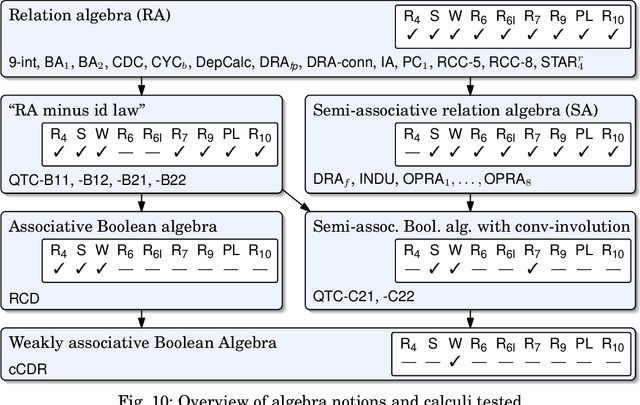
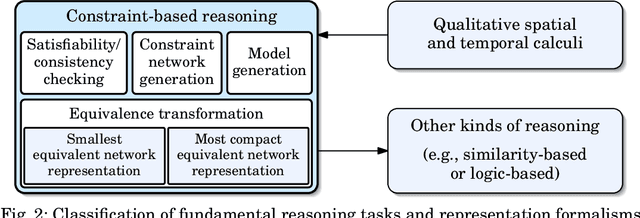
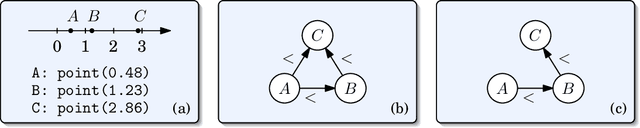
Qualitative Spatial and Temporal Reasoning (QSTR) is concerned with symbolic knowledge representation, typically over infinite domains. The motivations for employing QSTR techniques range from exploiting computational properties that allow efficient reasoning to capture human cognitive concepts in a computational framework. The notion of a qualitative calculus is one of the most prominent QSTR formalisms. This article presents the first overview of all qualitative calculi developed to date and their computational properties, together with generalized definitions of the fundamental concepts and methods, which now encompass all existing calculi. Moreover, we provide a classification of calculi according to their algebraic properties.

Algebraic Properties of Qualitative Spatio-Temporal Calculi

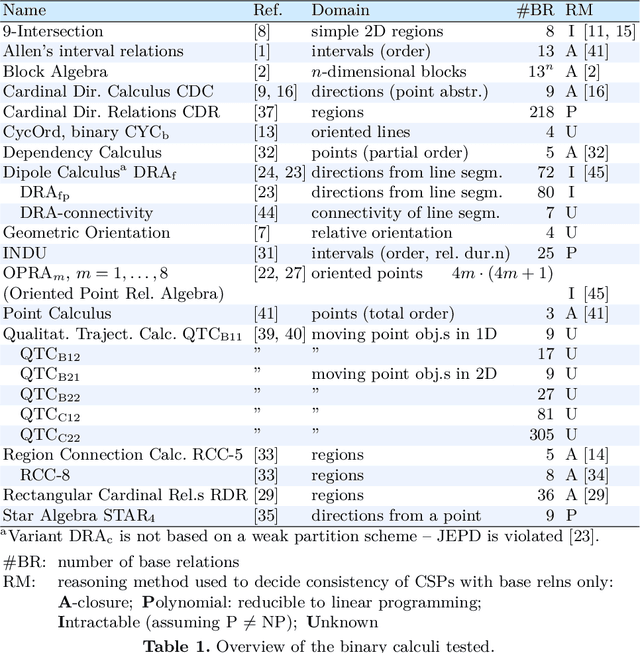
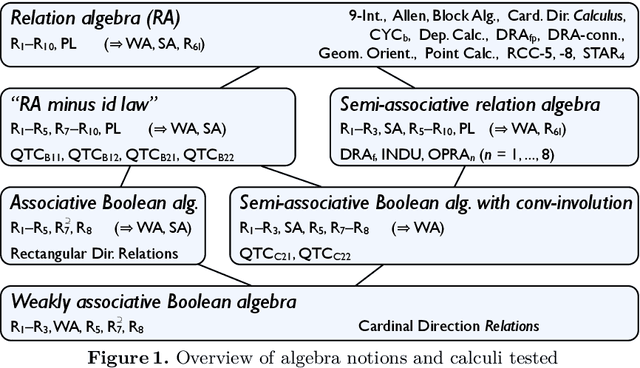
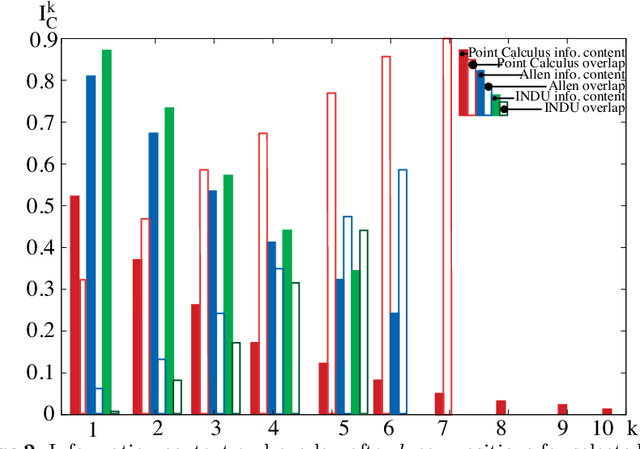
Qualitative spatial and temporal reasoning is based on so-called qualitative calculi. Algebraic properties of these calculi have several implications on reasoning algorithms. But what exactly is a qualitative calculus? And to which extent do the qualitative calculi proposed meet these demands? The literature provides various answers to the first question but only few facts about the second. In this paper we identify the minimal requirements to binary spatio-temporal calculi and we discuss the relevance of the according axioms for representation and reasoning. We also analyze existing qualitative calculi and provide a classification involving different notions of a relation algebra.